Федеральное агентство связи Российской Федерации
Государственное образовательное учреждение высшего профессионального образования
Сибирский Государственный Университет Телекоммуникаций и Информатики
Кафедра ТЭЦ
Курсовая работа по курсу ОТЦ
«Расчет электрических цепей при импульсном воздействии»
Выполнил: студент гр.В-67
Проверила:
Новосибирск 2008
Содержание
Введение…………………………………………………………………………...3
1) Техническое задание…………………………………………………………..4
2) Расчет напряжения на выходе цепи U2(t)
2.1 Переходная характеристика………………………………………………6
2.2 Интеграл Дюамеля……………………………………………………….10
3) Спектральная плотность сигналов………………………………………….13
4) Импульсная характеристика…………………………………………………20
5) Дискретизация………………………………………………………………..22
6) Спектральные характеристики дискретизированного сигнала…………...24
7) Z – преобразование импульсной характеристики цепи……………………26
8) Расчет дискретного сигнала…………………………………………………29
Заключение……………………………………………………………………….32
Список используемой литературы ……………………………………………..33
Введение
Цель курсовой работы состоит в систематизации и закреплении знаний, полученных при изучении классического, операторного и спектрального методов расчета процессов в линейных электрических цепях, а также теоретических основ анализа дискретных сигналов и линейных дискретных системах.
1.Техническое задание
Задание на курсовую работу содержит схему анализируемой цепи и входной сигнал в виде ограниченного импульса, параметры которого указаны на рисунке.
 |
Рисунок 1.1- Входной сигнал
Рисунок 1.2- Исходная цепь
Все резисторы схемы имеют сопротивление R=1кОм, емкость конденсаторов C=1мкФ.
В процессе выполнения необходимо получить следующие результаты:
1) рассчитать и построить график напряжения на выходе цепи Uвых(t);
2) вычислить передаточную функцию цепи H(jw), спектральную плотность сигнала на входе и выходе цепи, построить соответствующие графики;
3) используя импульсную характеристику цепи, получить выражение для передаточной функции;
4) провести дискретизацию входного сигнала и импульсной характеристики цепи, вычислить отсчёты дискретного сигнала на выходе и построить графики спектра дискретизированного сигнала и АЧХ дискретизированной цепи;
5) по отсчётам входного сигнала вычислить его спектральную плотность;
6) составить схему дискретной цепи, выполнив Z – преобразования дискретизированной импульсной характеристики;
7) определить передаточную функцию цепи, корректирующей искажения дискретного сигнала, вносимые сконструированной дискретной цепью, рассчитать дискретный сигнал на выходе корректора.
2. Расчет напряжения на выходе цепи U2(t)
2.1 Переходная характеристика
Интеграл
Дюамеля может быть получен, если аппроксимировать приложенное воздействие f1(t)
с помощью единичных функций, сдвинутых относительно друг друга на время ∆![]() .
.
Переходная характеристика:
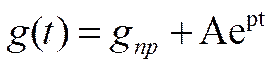 (2.1)
(2.1)
Где gпр = Uпр – переходная характеристика при t=∞
p- корень характеристического уравнения
 Включим
в цепь источник единичного напряжения:
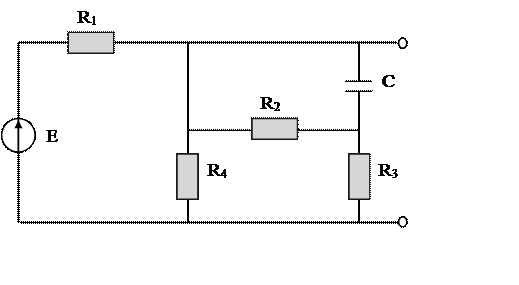
Включим
в цепь источник единичного напряжения:
|
||||||
Рисунок 2.1 – Цепь в установившемся режиме t=∞
Рассчитаем значения напряжений на элементах цепи при t=∞
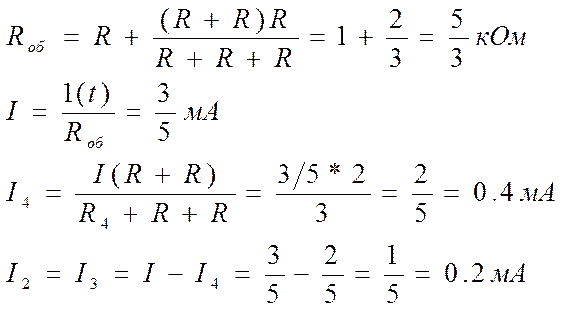
Uc = U2 = R*I2 = 0.2 В U3 = R*I3 = 0.2 В
gпр = U2(t=∞) = U2 +U3 = 0.4 В
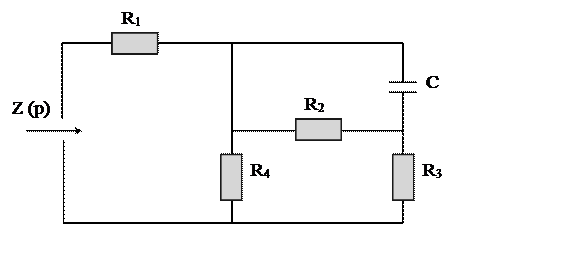 Нахождение
корня характеристического уравнения.
Нахождение
корня характеристического уравнения.
Рисунок 2.2 – Схема для определения корня характеристического уравнения
|
|
|
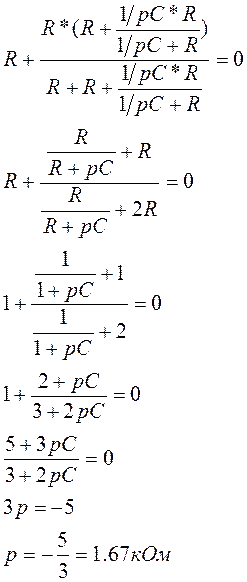
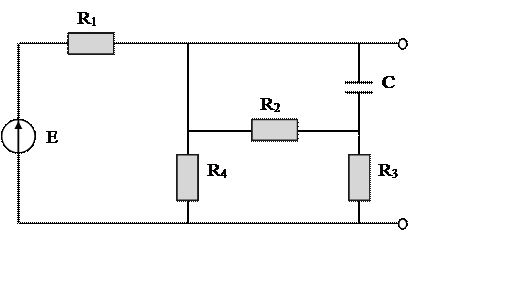
g(t) = 0.4 + Ae-5000t/3 = 0.4 + Ae-1670t
 Найдем А в момент времени t=0+
Найдем А в момент времени t=0+
Рисунок 2.3 – Цепь в момент времени t=0+
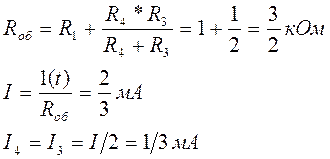
UC = 0 U2 = 0 U3 = 0.33 B
g(0+) =0.4+A=0.33
A= -1/15 = -0.0667
Общая формула для переходной характеристики:
g(t) =0.4-0.0667e-666.7t
В этом пункте была найдена переходная характеристика, с помощью которой можно произвести расчет напряжения на выходе подставляя ее в интеграл Дюамеля.
2.2 Интеграл Дюамеля.
 Весь
отрезок времени
Весь
отрезок времени ![]() разбивается на три
интервала. Границы интервалов приходятся на моменты времени
разбивается на три
интервала. Границы интервалов приходятся на моменты времени ![]() . Значение функции входного
сигнала
. Значение функции входного
сигнала ![]() на каждом из интервалов:
на каждом из интервалов:
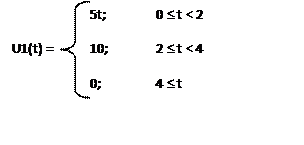 |
Рисунок 2.4 – Входной сигнал и его аналитическая запись
Первый интервал:
![]()
Второй интервал:
![]()
Сигнал на выходе найдём по интегралу Дюамеля.
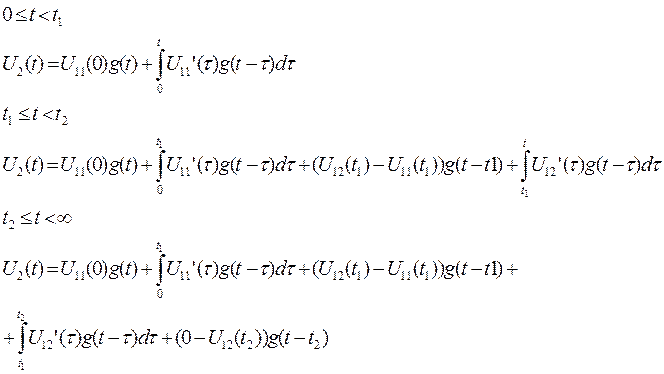 (2.2)
(2.2)
Вычисление выходного сигнала через интеграл Дюамеля:
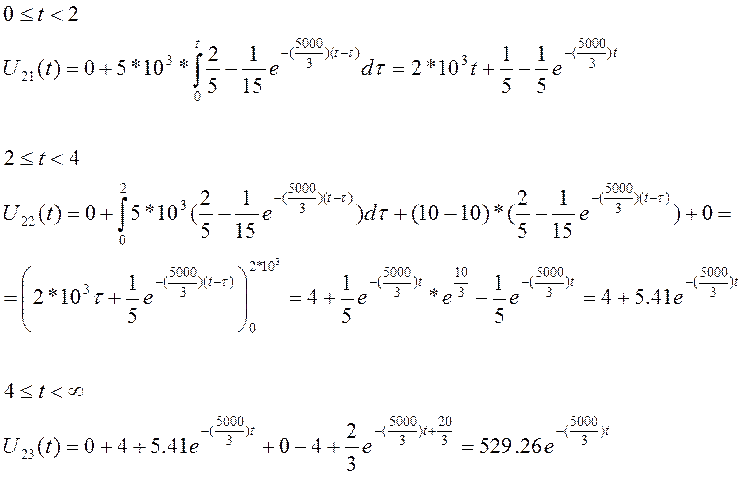
Таблица 2.1 -Значения U2(t), вычисленные с помощью интеграла Дюамеля
|
0≤t<2 |
2≤t<4 |
t≥4 |
|||
|
0 |
0 |
2 |
4.192996 |
4 |
0.673809 |
|
0.1 |
0.230704 |
2.1 |
4.163368 |
4.1 |
0.570367 |
|
0.2 |
0.456694 |
2.2 |
4.138288 |
4.2 |
0.482805 |
|
0.3 |
0.678694 |
2.3 |
4.117058 |
4.3 |
0.408686 |
|
0.4 |
0.897317 |
2.4 |
4.099088 |
4.4 |
0.345945 |
|
0.5 |
1.11308 |
2.5 |
4.083876 |
4.5 |
0.292836 |
|
0.6 |
1.326424 |
2.6 |
4.070999 |
4.6 |
0.24788 |
|
0.7 |
1.537719 |
2.7 |
4.0601 |
4.7 |
0.209826 |
|
0.8 |
1.747281 |
2.8 |
4.050873 |
4.8 |
0.177614 |
|
0.9 |
1.955374 |
2.9 |
4.043063 |
4.9 |
0.150347 |
|
1 |
2.162225 |
3 |
4.036452 |
5 |
0.127266 |
|
1.1 |
2.368024 |
3.1 |
4.030856 |
5.1 |
0.107728 |
|
1.2 |
2.572933 |
3.2 |
4.026119 |
5.2 |
0.09119 |
|
1.3 |
2.777088 |
3.3 |
4.022109 |
5.3 |
0.077191 |
|
1.4 |
2.980606 |
3.4 |
4.018715 |
5.4 |
0.065341 |
|
1.5 |
3.183583 |
3.5 |
4.015842 |
5.5 |
0.05531 |
|
1.6 |
3.386103 |
3.6 |
4.01341 |
5.6 |
0.046819 |
|
1.7 |
3.588237 |
3.7 |
4.011351 |
5.7 |
0.039631 |
|
1.8 |
3.790043 |
3.8 |
4.009609 |
5.8 |
0.033547 |
|
1.9 |
3.991571 |
3.9 |
4.008134 |
5.9 |
0.028397 |
|
2 |
4.192865 |
4 |
4.006885 |
6 |
0.024037 |
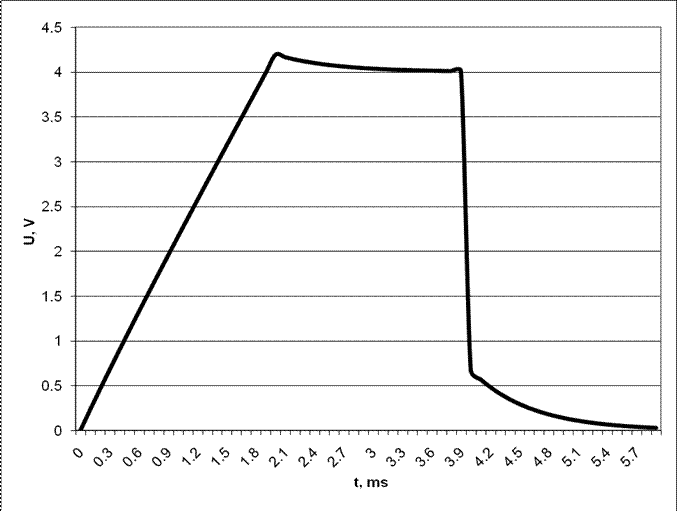
Рисунок 2.4 – График зависимости выходного сигнала от времени
В этом разделе рассчитали значения выходного сигнала в зависимости от времени и построил график этой зависимости.
3. Спектральная плотность сигналов
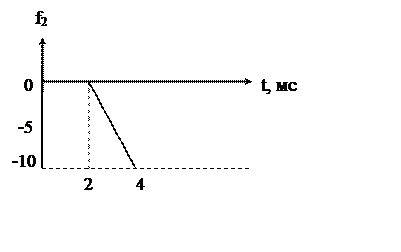
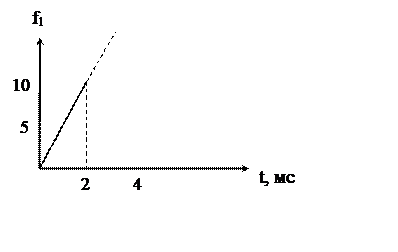 Для
нахождения спектральной плотности входного сигнала функция U1(t)
представляется в виде суммы «простейших» функций.
Для
нахождения спектральной плотности входного сигнала функция U1(t)
представляется в виде суммы «простейших» функций.
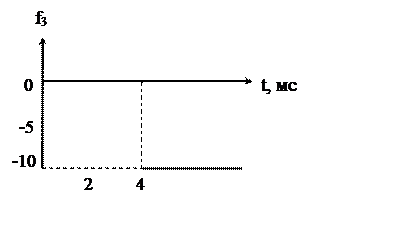
Рисунок 3.1 – Представление входного сигнала в виде суммы четырех функций времени
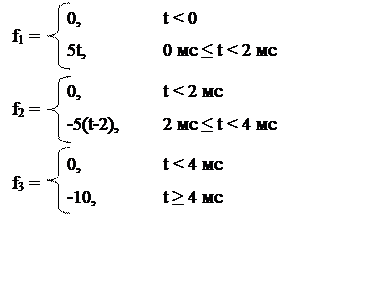 |
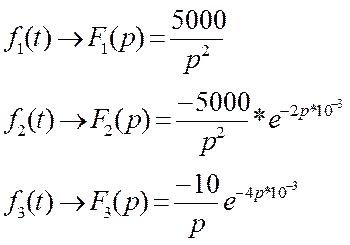
Изображение входного сигнала записывается как сумма изображений простейших функций
|
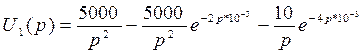
Заменяя
в последнем выражении ![]() получаем
спектральную плотность
получаем
спектральную плотность
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.