



















Наноэлектроника
Part four
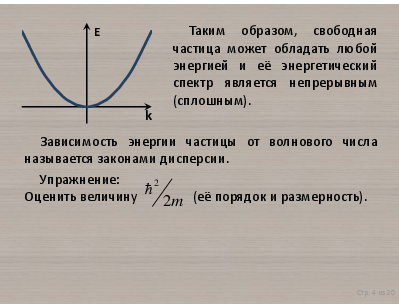
Физические основы наноэлектроники
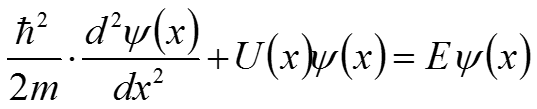
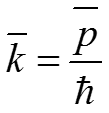
Стр. 2 из 20
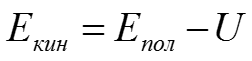
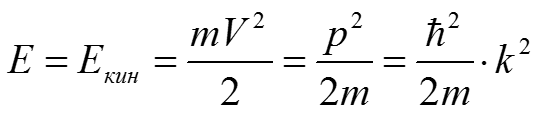
Стр. 3 из 20
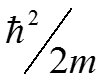
Стр. 4 из 20
Прохождение частицы через потенциальный барьер (туннельный эффект)
При рассмотрении механизма проводимости полупроводника иногда возникает такая ситуация, когда электроны просачиваются через достаточно высокие энергетические барьеры. В квантовой механике такое проникновение электронов через барьер оказалось вполне вероятно, причём энергия электрона при этом не изменится.0 Туннелирование – это явление проникновения электронов через потенциальный барьер в условиях, когда энергия электрона меньше высоты барьера.
Стр. 5 из 20
Туннельный эффект
Стр. 6 из 20
Туннельный эффект
Рассмотрим задачу: (7) Воспользуемся региональным методом решения задачи о нахождении волновых функций в отдельности для каждой из областей. Условия склейки на границе потенциального барьера должны обеспечивать непрерывность волновой функции в т. X=0, а также непрерывности производных этой функции.
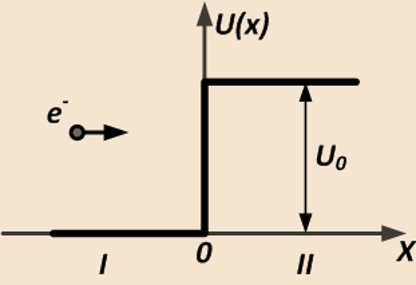
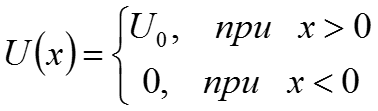
Стр. 7 из 20
Туннельный эффект
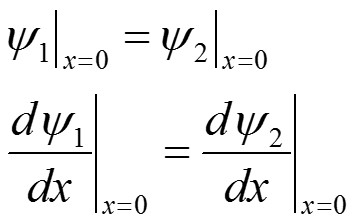
(8) Для нахождения волновой функции решим уравнение Шрёдингера (1) для каждой из областей: Для первой области: (9)
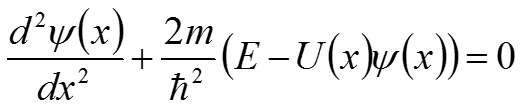
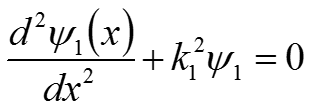
Стр. 8 из 20
Туннельный эффект где (10) Для второй области: (11) где (12) Уравнения (9) и (11) являются линейными дифференциальными уравнениями второго порядка. Общее решение для данных уравнений будет иметь вид:
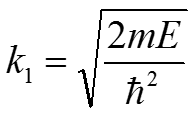
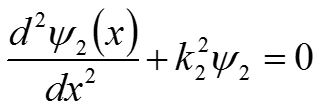
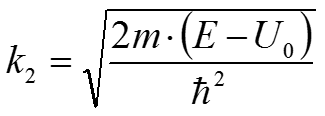
Стр. 9 из 20
Потенциальный барьер
Для первой области: (13) Для второй области: (14) где А1 и А2 – амплитуды падающих волн первой и второй областей соответственно; B1 и B2 – амплитуда отражённой волны в первой и второй областях. Так как во II области нет условий для возникновения отражённой волны ( ) примем В2 = 0
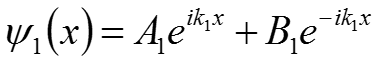
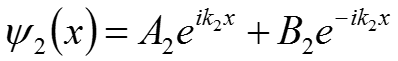
![]()
Стр. 10 из 20
Потенциальный барьер
Получим окончательные выражения для потенциального барьера. (15) Выразим амплитуды падающей о отражённой волны (B1 и A2 через амплитуду падающей волны (A1), на основе условия склейки: (16) (17)
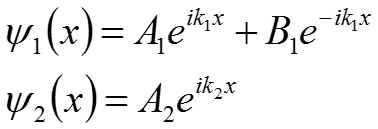
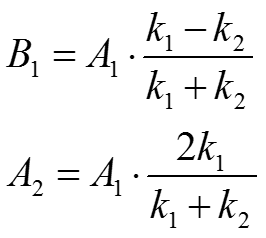
Стр. 11 из 20
Потенциальный барьер
В данной задаче имеет смысл ввести понятие коэффициента отражения частицы R и коэффициента прохождения через потенциальный барьер (прозрачности барьера) D: (18) где n – показатель преломления волны де Бройля: (19)
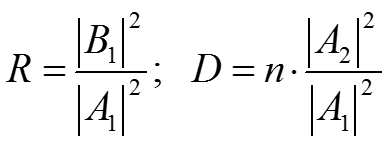
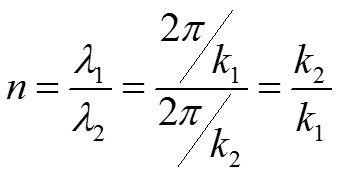
Стр. 12 из 20
Потенциальный барьер
Т.к. электрон либо отразится от потенциального барьера, либо пройдёт его: (20) Рассмотрим несколько случаев различного отношения высоты потенциального барьера и энергии летящей частицы:
![]()
Стр. 13 из 20
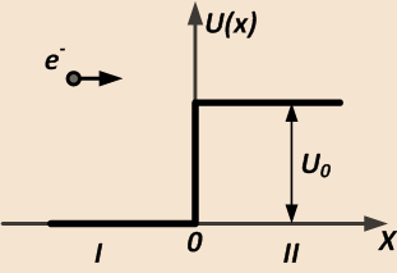
Низкий потенциальный барьер:
E>U0 В этом случае k2 (12) будет действительным числом: Коэффициенты отражения и прохождения в случае низного потенциального барьера равны:
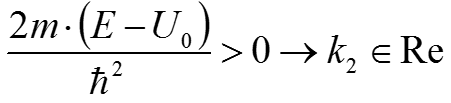
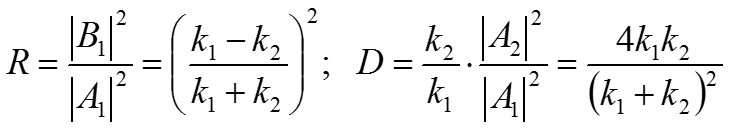
Стр. 14 из 20
Низкий потенциальный барьер:
В квантовой механике даже если потенциальный барьер ниже энергии частицы, существует вероятность того, что она отразится от барьера, в отличии от классической механики.
Стр. 15 из 20
Равенство высоты потенциального барьера и энергии электрона:
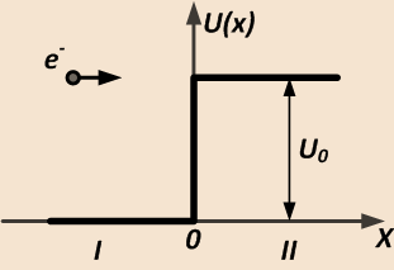
E=U0 В этом случае k2 (12) будет равен нулю: В этом случае волна будет полностью отражаться от барьера, прошедшей волны не будет:
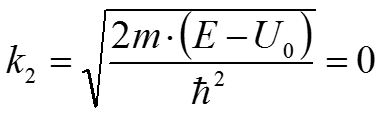
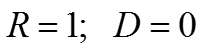
Стр. 16 из 20
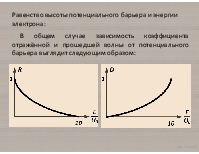
Равенство высоты потенциального барьера и энергии электрона:
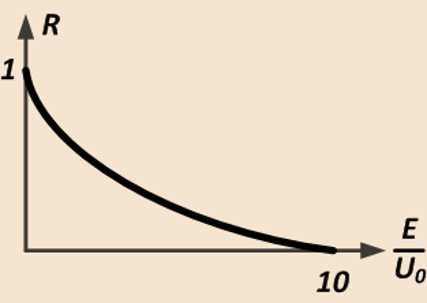
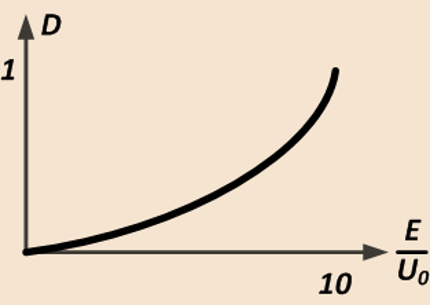
В общем случае зависимость коэффициента отражённой и прошедшей волны от потенциального барьера выглядит следующим образом:
Стр. 17 из 20
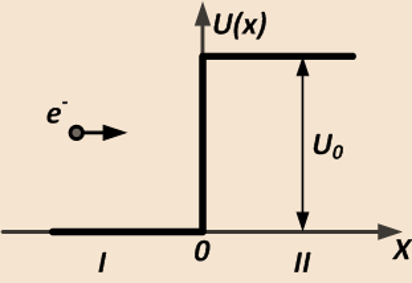
Высокий потенциальный барьер:
E<U0 В этом случае k2 (12) будет мнимым числом: Общее решение дифференциального уравнения (15) для второй области примет вид: Отличие Ψ2 от 0 означает, что существует отличная от 0 вероятность события, состоящая в том, что электрон проникнет в область II.
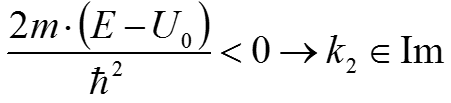
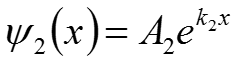
Стр. 18 из 20
Высокий потенциальный барьер:
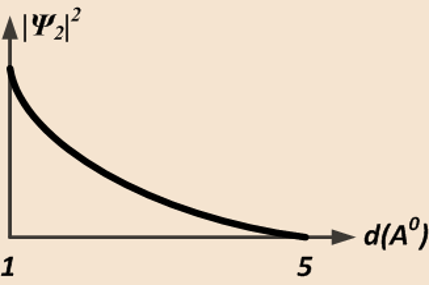
Т.о. эффективная величина проникновения частицы через барьер составляет величину, примерно равную Вывод: если толщина барьера порядка 1~3 А0 (атомарных расстояний), то потенциальный барьер будет обладать прозрачностью, несмотря на то, что энергия электрона меньше высоты барьера.
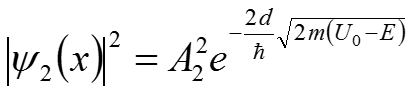
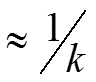
Стр. 19 из 20
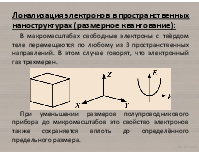
Локализация электронов в пространственных наноструктурах (размерное квантование):
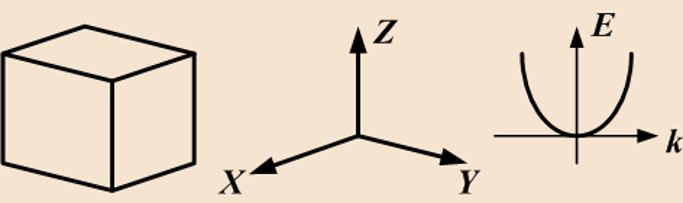
В макромасштабах свободные электроны с твёрдом теле перемещаются по любому из 3 пространственных направлений. В этом случае говорят, что электронный газ трехмерен. При уменьшении размеров полупроводникового прибора до микромасштабов это свойство электронов также сохраняется вплоть до определённого предельного размера.
Стр. 20 из 20
Локализация электронов в пространственных наноструктурах (размерное квантование):
В тех случаях, когда размеры объекта хотя бы по одному из пространственных направлений изменяются до наномасштабов, свойства трёхмерности электронного газа меняется. Эффектом локализации является эффект, возникающий при лимитировании движения электронов физическими размерами области, в которых они находятся. Эффект локализации наступает тогда, когда область локализации частиц сравнима или меньше их де Бройлевской волны.
Стр. 21 из 20
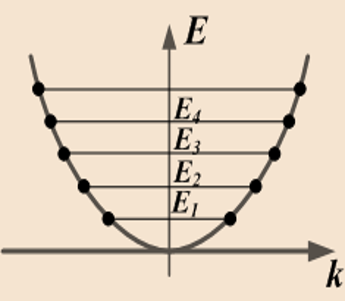
Локализация электронов в пространственных наноструктурах (размерное квантование):
Квантово-размерный эффект связан с квантованием импульса частицы вследствие чего непрерывный энергетический спектр распадается на дискретные уровни, т.е. происходит квантование энергии спектра частицы. В результате такого квантования электрофизические свойства электронов, например, удельное сопротивление образ-ца, начинает оссцилировать в зависимости от наноразмера образца.
Стр. 22 из 20
Спасибо за внимание
Стр. 23 из 18
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.