















МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ
Вятский Государственный Технический Университет
Кафедра строительных конструкций
___________________
Принял преподаватель
___________________
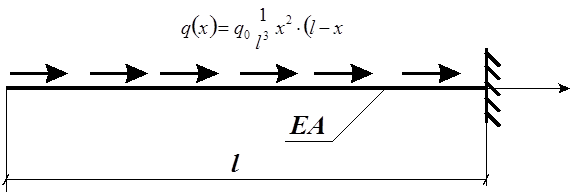 |
1. Точное решение
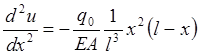 (1.1)
(1.1)
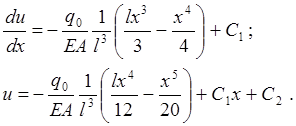 (1.2)
(1.2)
Удовлетворяем статические граничные условия (СГУ) при x=0:
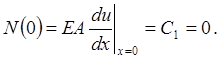 (1.3)
(1.3)
Удовлетворяем геометрические граничные условия (ГГУ) при x=l:
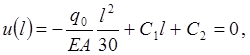 (1.4)
(1.4)
откуда, учитывая, что С1 =0, получим
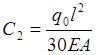 .
(1.5)
.
(1.5)
Внося найденные константы интегрирования в выражения для перемещения и продольного усилия, приходим к соотношениям:
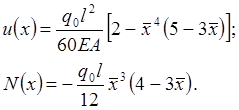 (1.6)
(1.6)
Здесь безразмерная координата
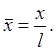 (1.7)
(1.7)
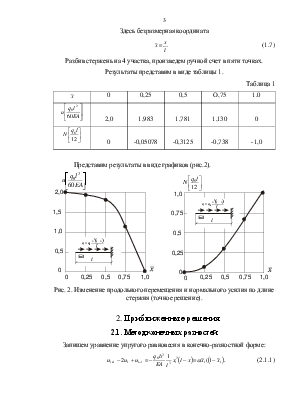
Разбив стержень на 4 участка, произведем ручной счет в пяти точках. Результаты представим в виде таблицы 1.
Таблица 1
|
|
0 |
0,25 |
0,5 |
O,75 |
1.0 |
|
|
2,0 |
1,983 |
1,781 |
1,130 |
0 |
|
|
0 |
-0,05078 |
-0,3125 |
-0,738 |
-1,0 |
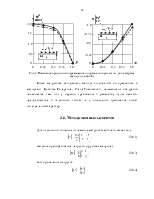
Представим результаты в виде графиков (рис.2).
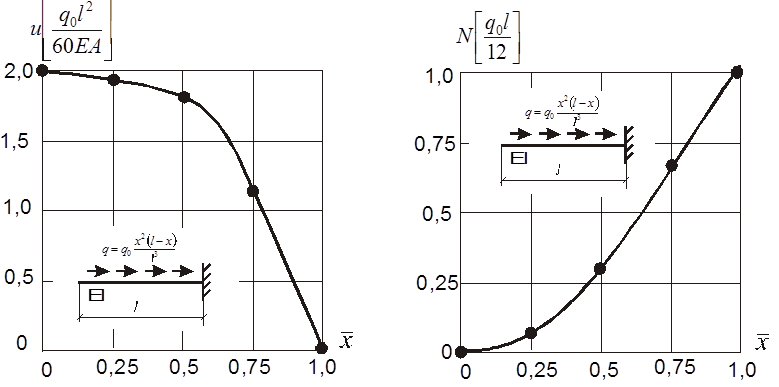
Рис. 2. Изменение продольного перемещения и нормального усилия по длине стержня (точное решение).
2. Приближенные решения
2.1. Метод конечных разностей
Запишем уравнение упругого равновесия в конечно-разностной форме:
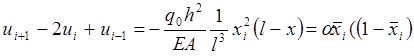 . (2.1.1)
. (2.1.1)
Здесь введено обозначение:
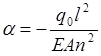 , (2.1.2)
, (2.1.2)
для нашего случая
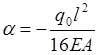 . (2.1.3)
. (2.1.3)
Так как на левом торце имеется статическое граничное условие, то введем законтурную точку u-1, тогда СГУ запишется так:
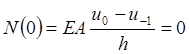 , (2.1.4)
, (2.1.4)
откуда
![]() . (2.1.5)
. (2.1.5)
Запишем уравнение упругого равновесия для всех внутренних точек (множитель α в правой части опускаем):
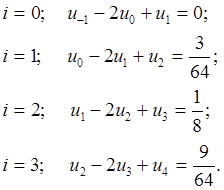 (2.1.6)
(2.1.6)
С учетом статического граничного условия на левом торце (2.1.4), следствия из него (2.1.5) и геометрического граничного условия на правом торце (u4=0) система (2.1.6) примет вид:
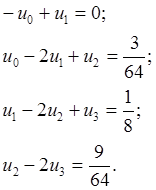 (2.1.7)
(2.1.7)
Выполним прямой ход, исключая неизвестные:
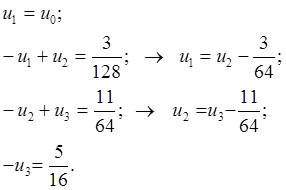 (2.1.8)
(2.1.8)
Выполним обратный ход:
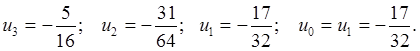 (2.1.9)
(2.1.9)
Ранее опущенный
множитель α с учетом вынесения в размерность 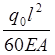 примет
вид:
примет
вид:
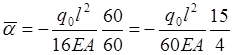 . (2.1.9)
. (2.1.9)
Найдем окончательные значения перемещений
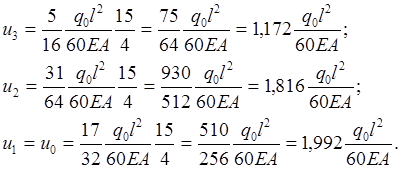 (2.1.10)
(2.1.10)
Перейдем к
продольному усилию, учитывая, что в точном решении в размерность было вынесено ![]() ,
,
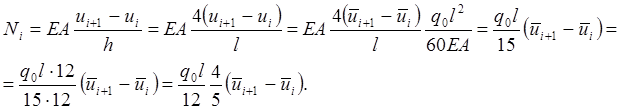 (2.1.11)
(2.1.11)
Черта сверху означает, что берутся только численные значения ui.
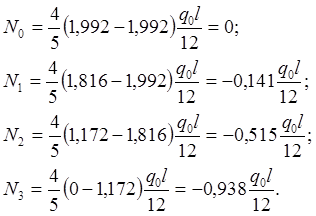 (2.1.12)
(2.1.12)
Осуществим переход от перемещений к усилиям с помощью дифференцирующей матрицы
![]() ,
(2.1.13)
,
(2.1.13)
или в развернутом виде:
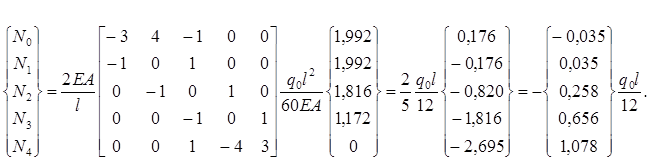 (2.1.14)
(2.1.14)
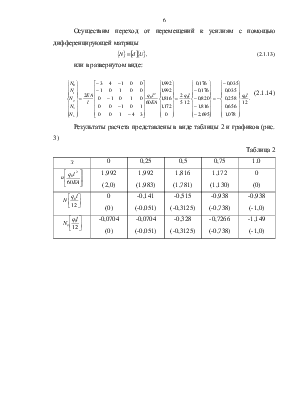
Результаты расчета представлены в виде таблицы 2 и графиков (рис. 3)
Таблица 2
|
|
0 |
0,25 |
0,5 |
0,75 |
1.0 |
|
|
1,992 (2,0) |
1,992 (1,983) |
1,816 (1,781) |
1,172 (1,130) |
0 (0) |
|
|
0 (0) |
-0,141 (-0,051) |
-0,515 (-0,3125) |
-0,938 (-0,738) |
-0,938 (-1,0) |
|
|
-0,0704 (0) |
-0,0704 (-0,051) |
-0,328 (-0,3125) |
-0,7266 (-0,738) |
-1,149 (-1,0) |
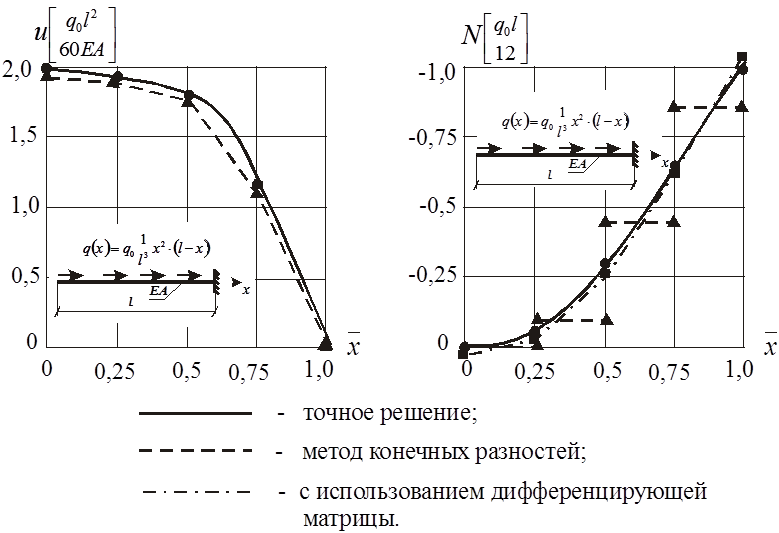 Рис. 3. Изменение продольного
перемещения и нормального усилия по длине стержня (метод конечных разностей).
Рис. 3. Изменение продольного
перемещения и нормального усилия по длине стержня (метод конечных разностей).
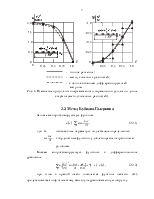
2.2. Метод Бубнова-Галеркина
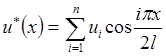 ,
(2.2.1)
,
(2.2.1)
где: ui – неизвестные параметры, подлежащие определению;
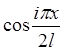 - координатные функции,
удовлетворяющие граничным условиям.
- координатные функции,
удовлетворяющие граничным условиям.
Внесем аппроксимирующую функцию в дифференциальное уравнение
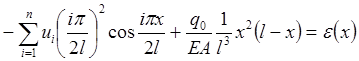 , (2.2.2)
, (2.2.2)
при этом в правой части появляется функция невязки e(x), представляющая по физическому смыслу неуравновешенную нагрузку.
Неизвестные
параметры будем определять из условия равенства нулю работы невязки на
возможных перемещениях, для чего умножим уравнение почленно на возможное
перемещение 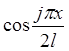 и проинтегрируем по длине стержня.
и проинтегрируем по длине стержня.
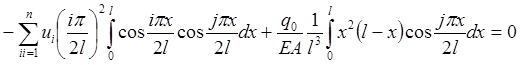 . (2.2.3)
. (2.2.3)
В силу ортогональности тригонометрических функций
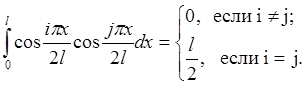 (2.2.4)
(2.2.4)
Остальные интегралы брались по частям:
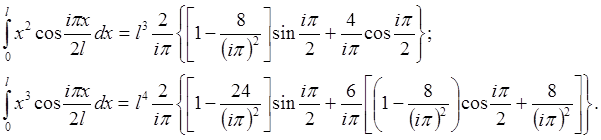 (2.2.5)
(2.2.5)
Внося значения интегралов в выражение для работы невязки на возможных перемещениях, приходим к равенству:
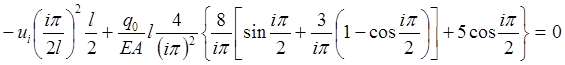 , (2.2.6)
, (2.2.6)
откуда
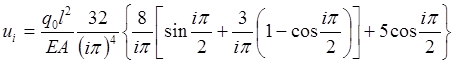 . (2.2.7)
. (2.2.7)
Выражение для перемещения принимает вид:
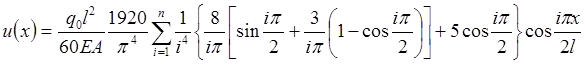 . (2.2.8)
. (2.2.8)
Дифференцируя по x и умножая на жесткость растяжения-сжатия EA, приходим к выражению для продольного усилия:
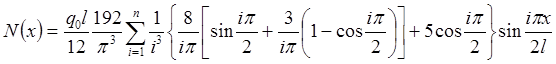 . (2.2.9)
. (2.2.9)
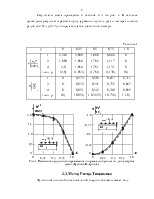
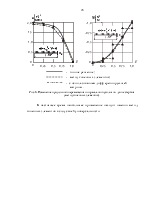
Результаты счета приведены в таблице 3 и на рис. 4. В таблице приведены результаты расчета при удержании одного, двух и четырех членов рядов (2.2.8) и (2.2.9), которые сходятся достаточно быстро.
Таблица 1
|
|
0 |
0,25 |
0,5 |
0,75 |
1.0 |
|
|
|
1 2 4 точн. р. |
2,262 1,990 2,0 (2,0) |
2,090 1,986 1,984 (1,983) |
1,600 1,792 1,781 (1,781) |
0,866 1,117 1,131 (1,130) |
0 0 0 (0) |
|
|
1 2 4 точн. р. |
0 0 0 (0) |
-0,272 -0,035 -0,051 (-0,051) |
-0,503 -0,321 -0,312 (-0,3125) |
-0,657 -0,755 -0,740 (-0,738) |
-0,711 -0,967 -0,995 (-1,0) |
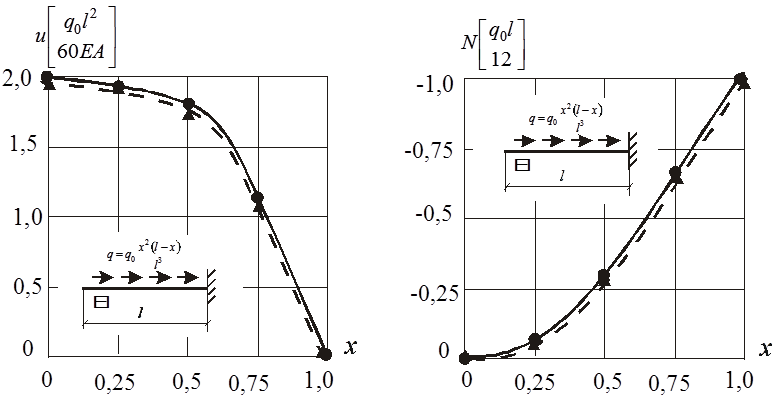 Рис. 4. Изменение
продольного перемещения и нормального усилия по длине стержня (метод
Бубнова-Галеркина).
Рис. 4. Изменение
продольного перемещения и нормального усилия по длине стержня (метод
Бубнова-Галеркина).
Функционал полной потенциальной энергии системы имеет вид:
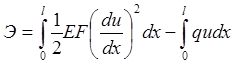 . (2.3.1)
. (2.3.1)
Внесем аппроксимирующую функцию (2.2.1) в выражение (2.3.1):
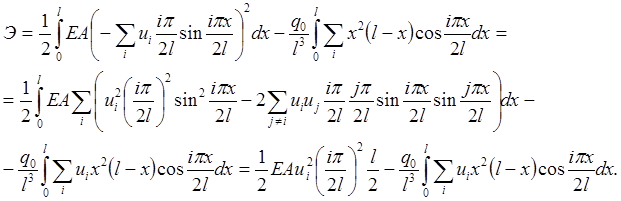 (2.3.2)
(2.3.2)
Запишем условие минимума функционала
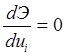 (2.3.3)
(2.3.3)
для (2.3.2)
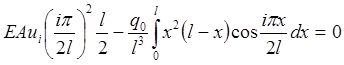 , (2.3.4)
, (2.3.4)
откуда
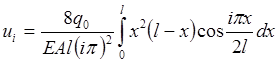 . (2.3.5)
. (2.3.5)
Внося значения интегралов (2.2.5) в (2.3.5), приходим к выражению для i–го неизвестного параметра
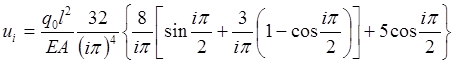 , (2.3.6) которое полностью
совпадает с (2.2.7). Совпадение решений, полученных методом Бубнова-Галеркина и
методом Ритца-Тимошенко объясняется тем, что аппроксимирующая функция бралась
одна и та же.
, (2.3.6) которое полностью
совпадает с (2.2.7). Совпадение решений, полученных методом Бубнова-Галеркина и
методом Ритца-Тимошенко объясняется тем, что аппроксимирующая функция бралась
одна и та же.
2.4. Метод наименьших квадратов
В методе наименьших квадратов мы имеем дело с функционалом, содержащим квадрат функции невязки (функционалом квадратичной ошибки)
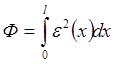 ,
(2.4.1)
,
(2.4.1)
который в нашем случае запишется так:
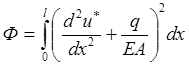 .
(2.4.2)
.
(2.4.2)
Внесем в этот функционал аппроксимирующую функцию (2.2.1)
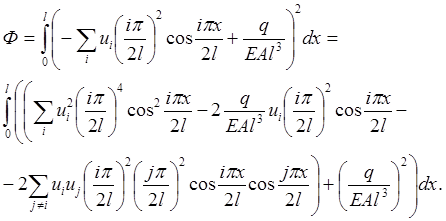 (2.4.3)
(2.4.3)
Учитывая условия ортогональности (2.2.4) и закон изменения внешней нагрузки, приходим к соотношению:
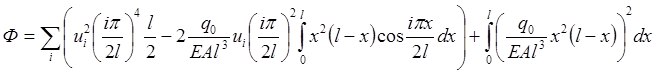 . (2.4.4)
. (2.4.4)
Условие минимума функционала квадратичной ошибки
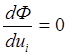 (2.4.5)
(2.4.5)
в применении к (2.4.4) приводит к выражению:
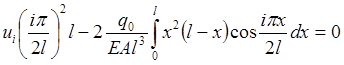 , (2.4.6)
, (2.4.6)
откуда
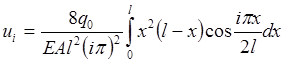 .
(2.4.7)
.
(2.4.7)
Полученное выражение полностью совпадает с (2.3.5). Таким образом, решения, полученные методами Бубнова-Галеркина, Ритца-Тимошенко и наименьших квадратов, одинаковы при одинаковых аппроксимирующих функциях.
2.5. Метод коллокаций
В методе коллокаций неизвестные параметры находятся из условия равенства нулю невязки в точках коллокации. Внесем аппроксимирующую функцию ( ) в дифференциальное уравнение
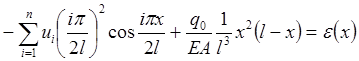 (2.5.1) и потребуем, чтобы невязка
(2.5.1) и потребуем, чтобы невязка ![]() была равна нулю в двух точках
коллокации при x=l/2 и x=l/4 ( очевидно, что при этом
число удерживаемых членов ряда должно быть равно числу точек коллокации):
была равна нулю в двух точках
коллокации при x=l/2 и x=l/4 ( очевидно, что при этом
число удерживаемых членов ряда должно быть равно числу точек коллокации):
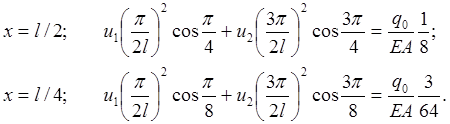 (2.5.2)
(2.5.2)
Перепишем систему уравнений, вынося общие множители в правую часть
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.