Цифровые фильтры. Основные понятия. Передаточные функции БИХ фильтров. Требования к частотным характеристикам фильтра

нормализованных соответствующим образом, где  вектор q_к есть вектор градиент целевой функции . Направление наискорейшего спуска определяется выражением:

Этот метод обладает свойством глобальной сходимости. Но к сожалению свойством глобальной сходимости не гарантирует практической э

Эффективности метода.

2.  Метод Ньютона

Этот метод является первым методом основанным на квадратичной аппроксимации целевой функции . Эта аппроксимация оставаясь достаточно простой, является более точной нежели линейная.

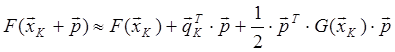
где G(x_к) - матрица Гессе, вектор q_к^T - вектор градиент.

Ньютоновское направление поиска вычисляется по следующей формуле:

В задачах поиска минимума произвольной квадратичной функции с положительно определённой матрицей Гессе метод Ньютона даёт решение за одну итерацию, не зависимо от выбора начального приближения. Длина шага h_К = 1. При применении метода Ньютона к нелинейной функции общего вида он обеспечивает высокую скорость сходимости (квадратичную). Данное обстоятельство позволяет считать метод Ньютона эталоном, с которым сравниваются другие алгоритмы. Тем не менее метод Ньютона может работать плохо или вообще расходиться если квадратичная функция плохо описывает поведение целевой функции в окрестности точки .

Итак если все матрицы G_К положительно определены и их числа обусловленности ограничены сверху, то применение Ньтоновского направления в комбинации с каким-либо алгоритмом вычисления длины шага даёт глобально сходящийся метод безусловной минимизации. При этом обязательно необходима регулировка длины шага, чтобы избежать пропуска точки минимума целевой функции.

Когда матрица Гессе перестает быть положительно определенной, то необходимым условием единственности решения является её невырожденность. Есть много методов основанных на методе Ньютона и работающих в отсутствии положительной определенности матрицы Гессе. Это модифицированные методы Ньютона.

3.  Модифицированные методы Ньютона

Общий принцип работы модифицированных методов Ньютона состоит в следующем: сначала конструируется связанная с матрицей Гессе  положительно определенная матрица , а затем направление поиска вычисляется также как и в методе Ньютона, но вместо матрицы Гессе в формуле используют вспомогательную матрицу. Процедура построения вспомогательной матрицы организуется т.о., чтобы  совпадала с исходной  если она является положительно определенной. При этом на каждом шаге выясняется все ли собственные значения матрицы  больше 0, а это за исключением случая диагональной матрицы Гессе, невозможно сделать по её виду.

К сожалению, данный метод не применим если - седловая точка.

Возможны несколько способов модификации метода Ньютона на основе матричных разложений (спектрального разложения, разложения Холеского).

4.  Квазиньютоновские методы

Теория квазиньютоновских методов опирается на возможность аппроксимации кривизны целевой функции  без явного формирования матрицы Гессе. Эта возможность вытекает из разложение вектора градиента