

гр 818
Индивидуальное задание №6
№=1; X=11; Y=12
В СМО типа M/M/1/![]() поступает поток заявок с
интенсивностью
поступает поток заявок с
интенсивностью ![]()
![]() ,
,
Среднее число обслуженных заявок
за 1 мин. равно ![]() .
.
![]() =11+0,1=11,1
=11+0,1=11,1
![]()
![]() =12+0,1=12,1
=12+0,1=12,1![]()
Определить:
а)среднюю длину очереди;
б)вероятность того, что в очереди находиться 0, 1, 2 заявки
в)Вероятность того, что вновь поступившей заявке совсем не придется ждать
г)среднее время ожидания в очереди
Для определения средней длины
очереди необходимо вычислить интенсивность трафика ![]() и
вероятность того, что все каналы свободны
и
вероятность того, что все каналы свободны ![]() .
.
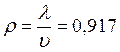 [эрл]
[эрл]
Для системы с n каналами и m местами в очереди:
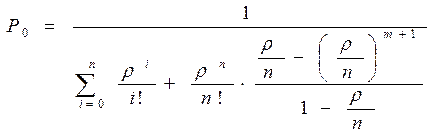
В нашем случае m=![]() (число мест в очереди не ограничено) и
число каналов n=1.
(число мест в очереди не ограничено) и
число каналов n=1.
Тогда 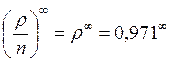 =0, с
учетом этого выражение для нахождения вероятности того, что канал свободен примет
вид:
=0, с
учетом этого выражение для нахождения вероятности того, что канал свободен примет
вид:
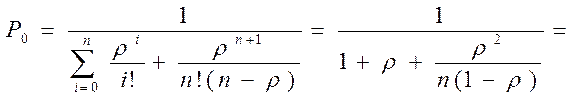
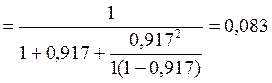
a)определить
среднюю длину очереди ![]()
средняя длинна очереди для n-канальной системы с m количеством мест в очереди:
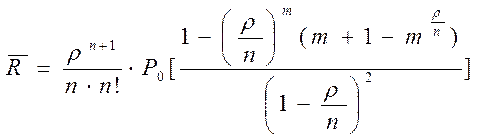
Упростим с учетом n=1, m=![]() и
и 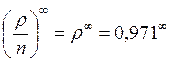
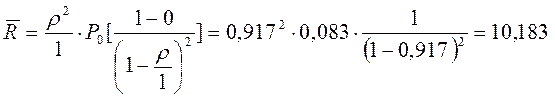
Т.е в среднем в очереди находиться приблизительно 10 заявок
б)вероятность того, что в очереди находиться 0, 1, 2 заявки
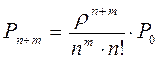
![]() - есть вероятность того, что все n каналов и m мест
в очереди занято
- есть вероятность того, что все n каналов и m мест
в очереди занято
Для одноканальной СМО
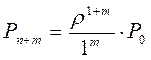
Найдем вероятность того, что в очереди нету заявок т.е. m=0
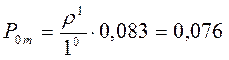
Вероятность того, что в очереди одна заявка т.е. m=1
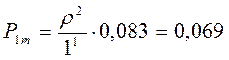
вероятность того, что в очереди две заявка т.е. m=2
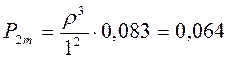
г)среднее время ожидания в очереди
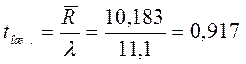
[мин] т.е. примерно 55 секунд
в)Вероятность того, что вновь поступившей заявке совсем не придется ждать
ситуация возможна в случае когда канал свободен и когда в очереди нету заявок
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.