

|
N |
4 |
128 |
1024 |
8192 |
|
КУВ |
4 |
35,6 |
205 |
1263 |
Не всегда удобно использовать БПФ, т. к. часто нас интересует не весь спектр, а только его часть, где мы ожидаем найти спектр сигнала, например, по результатам предварительных вычислений, то удобней использовать ДПФ.
Чаще всего эта процедура состоит из двух этапов: сначала вычисляется БПФ с небольшим числом отсчетов, и по результатам находят грубо положение максимума спектра. Затем в области этого максимума выполняется ДПФ с добавлением нулевых отсчетов к исходным отсчетам сигнала, чтобы улучшить детальность спектра.
Разновидности БПФ
Существует много вариантов БП
каждый из которых имеет свой способ организации вычислений и позволяет получить
дополнительный выигрыш в скорости вычислений для конкретной ситуации. В основе
всех этих методов в основном лежит принцип разделения исходного N точечного ДПФ к вычислению
нескольких ДПФ меньшей размерности. Самый простой вариант использование
последовательности отсчетов, размерность которых определяется как ![]() . Это прореживание по частоте и
прореживание по времени.
. Это прореживание по частоте и
прореживание по времени.
По эффективности оба этих метода эквивалентны и позволяют уменьшить число требуемых арифметических операций.
Алгоритм с прореживанием по частоте заключается в простом разделении сигнала пополам.
РИСУНОК СИГНАЛА
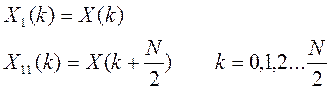
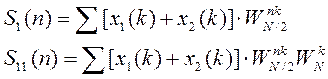
Каждый из этих массивов еще может делиться пополам (пока не будет по 2 отсчета)
Особенностью этих 2-х алгоритмов заключается в том, что когда мы делаем прореживание по отсчетам, мы должны переставить их в двоично-инверсном порядке, но отсчеты спектра получаются в естественном порядке. Если же мы делаем прореживание по частоте, то в результате расчета отсчеты спектра получаются в двоично-инверсном порядке, т.е. надо выполнить такую же перестановку.
Следующей разновидностью БПФ
является алгоритм для произвольно составленного N ![]() . В этом случае
(
. В этом случае
(![]() - целые положительные числа) вычисление
ДПФ (n – точечного) сводится к
тому, что мы
- целые положительные числа) вычисление
ДПФ (n – точечного) сводится к
тому, что мы ![]() раз вычислим
раз вычислим ![]() точечное ДПФ и затем
точечное ДПФ и затем ![]() раз вычислим
раз вычислим ![]() точечное
ДПФ.
точечное
ДПФ.
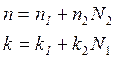
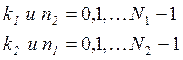
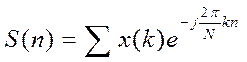
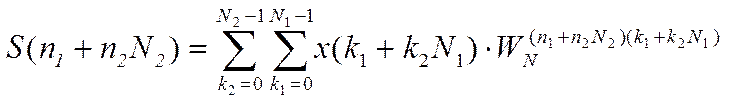
Упростим выражение
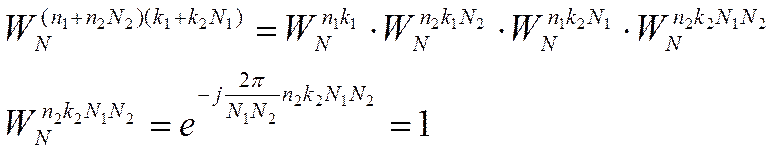
Получим что
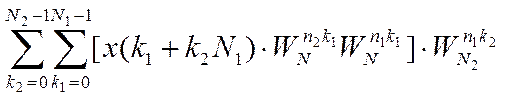
РИСУНОК ПРИМЕРА
Особенности практической реализации БПФ
Анализируя направленный граф БПФ можно выявить два аспекта:
1. доступ к данным и запоминание промежуточного результата
2. конкретный способ вычислений типа бабочка
Как правило, во всех алгоритмах БПФ вычисления выполняются с запоминанием промежуточного результата в тех же ячейках, что и исходный массив. Это делается для экономии памяти. Отсчеты спектра получаются в естественном порядке. Если нам не нужен естественный порядок, то эту перестановку можно не делать (использовать прореживание по частоте) т.к. в ряде задач требуется вычислить спектр, затем что-то с ним сделать, а потом сделать ОБПФ, чтобы получить отфильтрованный сигнал.
Другая особенность состоит в
том, что при вычислении алгоритма бабочка мы должны каждый раз вычислять
комплексный множитель ![]() . Его надо вычислять на каждом
шаге или заранее рассчитывать и запоминать в виде таблицы.
. Его надо вычислять на каждом
шаге или заранее рассчитывать и запоминать в виде таблицы.
![]() -
рекурсивная формула
-
рекурсивная формула
Но необходимо помнить, что если мы используем вычисления с конечной точностью, то при итерационных вычислениях ошибка может нарастать. Во избежание этого надо использовать те точки, где функции известны.
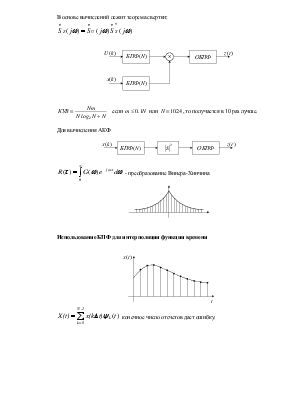
Вычисление корреляционного интеграла на основе БПФ
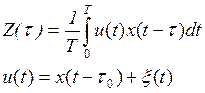
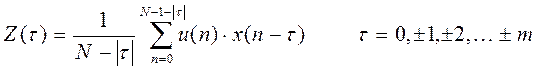
Если ![]() , то
, то 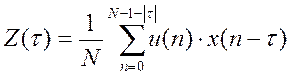 , где
, где ![]() - номер
отсчета во время сдвига
- номер
отсчета во время сдвига
В основе вычислений лежит теорема свертки:
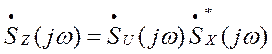
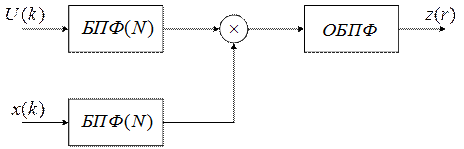
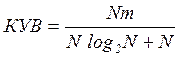 если
если
![]() или
или ![]() , то
получается в 10 раз лучше.
, то
получается в 10 раз лучше.
Для вычисления АКФ

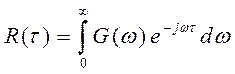 -
преобразование Винера-Хинчина
-
преобразование Винера-Хинчина
Использование БПФ для интерполяции функции времени
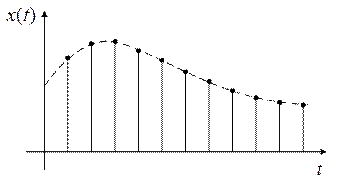
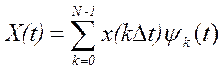 конечное
число отсчетов дает ошибку.
конечное
число отсчетов дает ошибку.
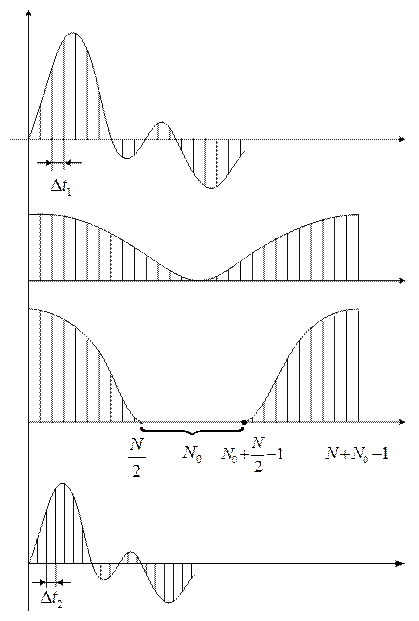
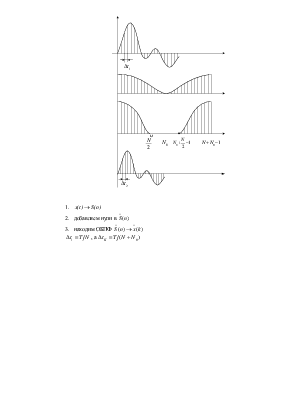
1. ![]()
2. добавляем
нули в ![]()
3. находим
ОБПФ ![]()
![]() , а
, а ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.