Модуль вращательного ускорения точки твердого тела. Центростремительное и полное ускорение

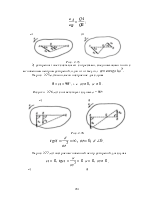
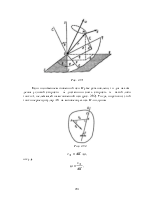
совершающего плоское движение, имеют параллельные скорости

см/с.

Вектор  перпендикулярен ОА и направлен в сторону , скорость точки В направлена вдоль горизонтали. Мгновенный центр скоростей звена АВ в этом случае находится в бесконечности, поэтому  (рис. 2.80,б).

Для определения положения мгновенного центра ускорений Q необходимо знать ускорение одной точки плоской фигуры, ее угловую скорость и угловое ускорение.

Определим ускорение точки А. Точка А одинаково принадлежит и звену АВ,и  звену ОА, вместе с которым совершает вращение вокруг оси, проходящей через точку О.

, где  - центростремительное ускорение точки, направленное к центру вращения, модуль которого определяется равенством

м/с²;

где   - вращательное ускорение, которое в случае равномерного вращения равно нулю .

Таким образом,  .

Обозначим угловое ускорение шатуна АВ  и определим положение мгновенного центра ускорений из равенства

,    .

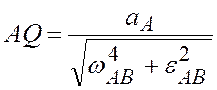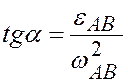Но , тогда  .

Следовательно, мгновенный центр ускорений лежит на прямой, перпендикулярной ускорению точки А и проходящей через эту точку. Одновременно мгновенный центр ускорений лежит на прямой, проведенной через точку В перпендикулярно ускорению этой точки. Точка  В  движется поступательно вдоль горизонтали, ускорение точки В также направлено по горизонтали.

Зная положение мгновенного центра ускорений шатуна, можно найти ускорение точки А, как точки, принадлежащей этому звену,

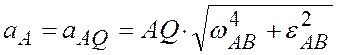, с учетом того, что , имеем

.

Подставляя значение , находим угловое ускорение шатуна

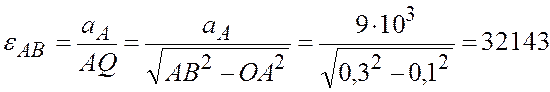 рад/с².

Угловое ускорение покажем на рис. 2.80,б против хода часовой стрелки, т.е.  в соответствии с направлением отсчета угла . Ускорение точки В будет

 м/с².

Ускорение точки С

 м/с².

На рис. 2.80,б ускорения точек В и С перпендикулярны отрезкам BQ и CQ соответственно и направлены в сторону углового ускорения  .

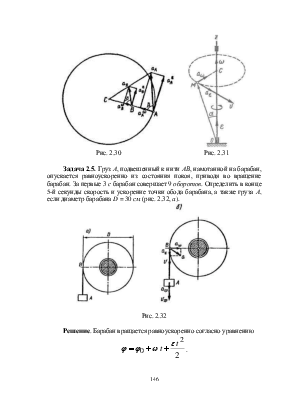
Задача 2.17. Определить скорость и ускорение точки В линейки эллипсографа АВ длиной 40 см  в момент, когда a= 30^о, если скорость точки А  = 2 м/с, ускорение = 0,6 м/с² и направлены так, как показаны на чертеже (рис. 2.81,а).

Решение. Кинематический анализ механизма. Тело АВ совершает плоское движение, при этом две точки движутся по изображенным пунктиром прямолинейным траекториям.

а)                                                     б)

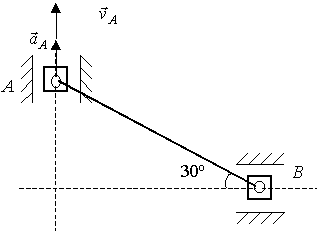
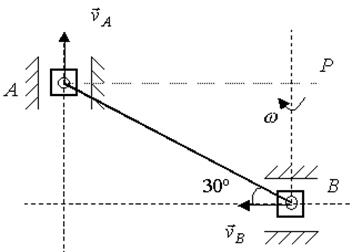
Рис. 2.81

Скорость точки А изображена на рисунке, а скорость точки В будет направлена вдоль горизонтальной прямой, являющейся ее траекторией. Так как рассматривается плоское  движение, то определим положение мгновенного центра скоростей, проведя перпендикуляры через две точки плоской фигуры к скоростям этих точек (рис. 2.81,б).

Мгновенные радиусы РА и РВ определим следующим образом:

м;

м.

2. Определение скорости точки В

.                                               (а)

Угловая скорость по условию задачи неизвестна, точка А, скорость которой задана, вместе с телом АВ поворачивается вокруг мгновенного центра скоростей и ее скорость   можно записать в виде

, откуда

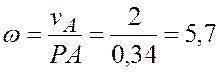рад/с.

Вектор скорости  направлен в сторону угловой скорости w, т.е. поворот плоской фигуры АВ вокруг МЦС  осуществляется по ходу часовой стрелки. Подставляя значение w в выражение (а), находим модуль :

 м/с.

Вектор  изобразим перпендикулярно мгновенному радиусу, т.е. вдоль траектории в сторону w.

3. Определение ускорения точки В. В соответствии с теоремой об ускорениях точек плоской фигуры ускорение точки В равно геометрической сумме  ускорения полюса и ускорения данной точки во вращении вместе плоской фигурой вокруг полюса. За полюс примем точку А, ускорение которой известно из условия задачи.

.

Составляющее ускорение  , в свою очередь, состоит из двух слагаемых:

, тогда

.                                              (б)

Определим значения составляющих ускорений:

 м/с²;      .

Угловое ускорение плоской фигуры e равно первой производной по времени от угловой скорости w

.

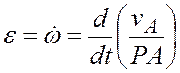Закон изменения мгновенного радиуса РА неизвестен, подсчитано только значение в данный момент времени, поэтому выражение для угловой скорости продифференцировать невозможно, т.е. определить угловое ускорение e ,  а следовательно,  и   нельзя.

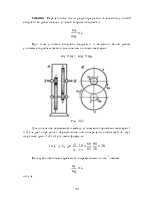
Для определения ускорения   выполним следующее построение (рис. 2.82):   вектор ускорения полюса изобразим в точке В;  покажем вдоль АВ, направив его к полюсу;   направим перпендикулярно  в любую сторону (покажем его предположительное