Определение усилий в стержнях фермы методом сечений. Рычаг. Сцепление и трение скольжения. Устойчивость при опрокидывании. Коэффициент устойчивости

уравнение проекций и два уравнения моментов, причем в качестве моментных точек нужно взять точки пересечения линий действия неизвестных усилий.

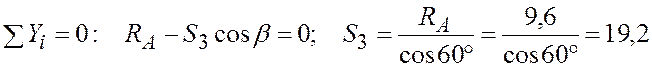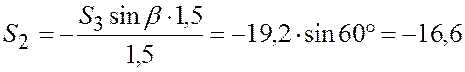кН;

;

кН.

Сечение 2-2.  Рассекать ферму на части можно не только вертикально, важно, чтобы при этом в сечение попадали только три стержня. При проведении сечения 2-2 менее трудоемким будет изображение правой отсеченной части (рис. 1.78).

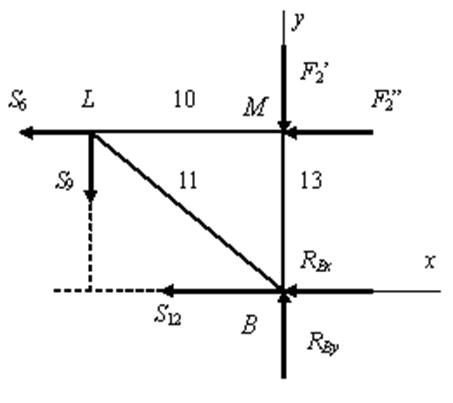
Рис. 1.78

Уравнения равновесия будут выглядеть следующим образом:

;

;

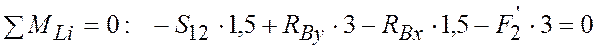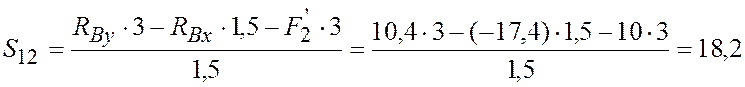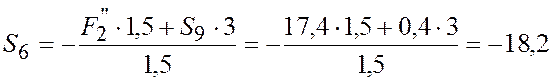кН;

кН.

Глава  8. Рычаг. Сцепление и трение скольжения

8.1.  Рычаг. Устойчивость при опрокидывании.

Коэффициент устойчивости

Рычагом называется твердое тело, имеющее неподвижную ось вращения и находящееся под действием сил, лежащих в плоскости, перпендикулярной этой оси.

Положим, что к рычагу в точках   приложены задаваемые силы ,  лежащие в плоскости чертежа, а ось рычага пересекает эту плоскость в точке О, которую называют опорной точкой (рис.  1.79). Реакция  оси рычага, уравновешивая задаваемые силы, лежит в их плоскости, но направление ее не  известно.

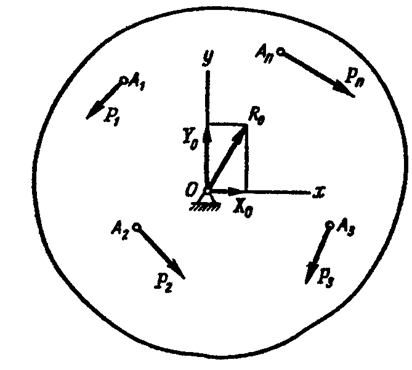
Рис. 1.79

Уравнение моментов задаваемых сил относительно опорной точки, не содержащее реакции оси рычага, выражает условие, которому удовлетворяют задаваемые силы, приложенные к рычагу, если он находится в покое.

Это условие формулируется так: если рычаг находится в покое, то алгебраическая сумма моментов всех задаваемых сил, приложенных к рычагу, относительно опорной точки равна нулю

.

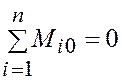Из этого условия, которое выполняется, если рычаг находится в покое, получим условие устойчивости тел при опрокидывании.

Пусть к прямоугольному параллелепипеду (рис. 1.80) весом на высоте d приложена горизонтальная сила , которая может не только сдвинуть тело, но и опрокинуть его при вращении вокруг ребра А. Считая, что сила  недостаточно велика, чтобы сдвинуть тело, рассмотрим ее опрокидывающее действие. Обозначим а расстояние от точки А, изображающей на чертеже ось вращения рычага, до линии действия силы , которая препятствует опрокидыванию. Составим сумму моментов задаваемых сил   и  относительно опорной точки  А

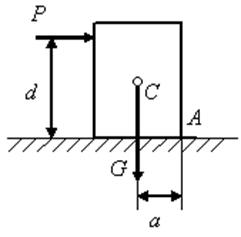
Рис. 1.80

, откуда     .

Назовем абсолютные значения моментов сил  и   относительно точки  А   удерживающим и опрокидывающим моментами:

.

Тогда на границе устойчивости

                        .

При устойчивом состоянии тела

                      .

          Устойчивость при опрокидывании в технике принято определять отношением числового значения удерживающего момента к числовому значению опрокидывающего момента:

.

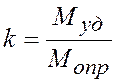Это отношение называют коэффициентом устойчивости. Очевидно, что в случае предельной устойчивости коэффициент устойчивости k= 1, а в случае устойчивого состояния k > 1.

Определить, опрокинется ли тело под действием силы или будет находиться в устойчивом состоянии, можно и графическим путем. Для этого продолжим линии действия сил  и  до их пересечения в точке К, перенесем силы в эту точку и найдем их равнодействующую (рис.  1.81).

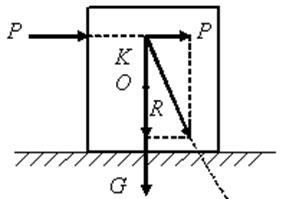
Рис. 1.81

Продолжая линию действия равнодействующей силы, найдем точку ее пересечения с опорной плоскостью. В рассмотренном примере возможны три случая.

1. Если эта точка лежит слева от ребра А, то состояние тела устойчиво.

2. Если линия действия равнодействующей пересекает ребро А, то состояние тела предельно устойчиво.

3. Если эта точка лежит справа от ребра А, то тело опрокинется.

8.2. Сцепление и трение скольжения

Если к твердому телу, покоящемуся на шероховатой горизонтальной плоскости (рис. 1.82), приложить горизонтальную силу , то действие этой силы вызовет появление силы сцепления , представляющей