совокупность всех возможных амплитуд перехода из одного состояния квантовой системы в другие. Сама вероятность перехода пропорциональна квадрату амплитуды, точнее, квадрату модуля амплитуды. Именно такие амплитуды перехода и наблюдаются на опыте. В таком представлении каждая величина имеет два индекса, определяющих начальное н конечное состояния системы. Эти величины называются матрицами. Так, координате q соответствует матрица — совокупность матричных элементов qnm, где n и m – два состояния системы. Гейзенберг получил замкнутые уравнения, из которых в принципе можно найти все наблюдаемые величины. Однако в своей первоначальной форме матричная механика Гейзенберга казалась неоправданно сложной по сравнению с волновой механикой Шредингера, о которой мы сейчас будем говорить.
Вот как выглядит уравнение Шредингера для одномерного движения в потенциале V (х):
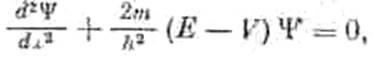
Решения этого уравнения для V = 0 очень легко найти. Их два: y1 = a sin kx и y2 = b cos kx. Они и описывают волны де Бройля:
k = 2πλ, λ= hp.
Решения уравнения Шредингера для связанных состояний, когда вероятность найти частицу вдали от удерживающего ее поля мала, следует искать при условии, что волновая функция У достаточно быстро стремится к нулю на больших расстояниях. При этом решение в кулоновском потенциале атома водорода существует не для всех энергий, а только для определенных дискретных значений, совпадающих с теми, которые получились из боровских правил квантования.
Становится ясным смысл правил квантования Бора — Зоммерфельда: допустимые значения энергии соответствуют требованию, чтобы в области движения частицы уместилось целое число волн де Бройля.
Уже в 1926 году Шредингер показал полную эквивалентность волновой и матричной механик, которые объединились в квантовую механику.
В 1927 году американские физики Дэвиссон и Джермер и независимо от них англичанин Уильям Томсон (сын знаменитого Дж. Дж. Томсона, впервые исследовавшего электрон) открыли дифракцию электронов на кристаллах. Таким образом, подтвердилась не только волновая природа электрона, но и выражение для длины волны де Бройля.
Опыты по дифракции электронов тоже описываются уравнением Шредингера, если предположить, что интенсивность пучка электронов после рассеяния пропорциональна квадрату модуля волновой функции. Там, где волны, рассеянные атомами кристаллической решетки, складываются, получается максимальная интенсивность электронного пучка.
При уменьшении интенсивности пучка обнаруживается, что дифракционная картина не изменяется, даже если пролетает, скажем, один электрон в минуту. Значит, уже одному электрону следует приписать вероятность попасть в то или иное место фотопластинки, стоящей за кристаллом.
Сначала предполагали, что волновым свойствам частицы соответствует некое реальное физическое поле, подобно электромагнитному полю в световой волне. Но тогда уже один электрон давал бы в одном акте всю дифракционную картину, а он чернит только одно зерно фотопластинки. И это был не единственный довод против такого взгляда на природу волнового процесса.
Анализ мысленных опытов по интерференции волн де Бройля (пучок электронов, падая на экран с двумя отверстиями, должен дать
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.