Волновая механика. Статистическая интерпретация понятия. Кинематическое и механическое соотношение, страница 3

К созданию волновой механики Эрвин Шредингер пришел, рассматривая атом как колебательную систему и отождествляя возможные собственные колебания системы с устойчивыми энергетическими состояниями в атоме. Близкое знакомство с теорией колебаний помогло Шредингеру сформулировать основную физическую идею в рамках задачи о собственных значениях дифференциального уравнения.

Поскольку гипотеза де Бройля о волновых свойствах вещества базировалась на положениях специальной теории относительности, то и Шредингер, естественно, использовал в своих рассуждениях релятивистский подход. В результате интенсивной работы ему удалось, наконец, преодолеть многочисленные математические трудности и вывести — это случилось в последние дни декабря 1925 г. — релятивистское волновое уравнение в виде, в котором оно известно теперь как уравнение Клейна — Гордона:

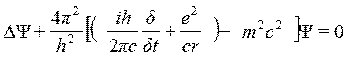
где с — скорость света, m— масса электрона, е — элементарный заряд, г — расстояние между электроном и ядром, y — волновая функция, Δ — оператор Лапласа.

Это релятивистское уравнение Шредингера, однако, не привело к ожидаемому успеху, поскольку согласие с экспериментальными данными было далеко не полным. Энергетические уровни атома водорода, стандартного объекта атомной физики, определялись лишь весьма приблизительно; особенно плохо обстояло дело с тонкой структурой водородных линий. Причина этого, впрочем, крылась не столько в полученных Шредингером результатах, сколько в общем уровне тогдашних физических знаний. Выведенное Шредингером уравнение абсолютно точно описывало поведение частиц, лишенных спина; в случае же электрона необходимо было ввести поправку, учитывающую спин. В то время, однако, об этом еще не было известно: исследования, приведшие к открытию спина электрона, тогда как раз лишь начинались.

Итак, надежды Шредингера разрешить загадку атомной механики поколебались, но отнюдь не рухнули. Судя по всему, он по-прежнему был убежден в правильности избранного им пути: на рубеже 1925/26 г. он направил в редакцию «Annalen der Physik» рукопись, в которой излагались его попытки и приводилось релятивистское волновое уравнение ([62], с. 96). Уверенность Шредингеру придавало то обстоятельство, что полученные результаты были «хотя бы отчасти верны»: нерелятивистская формула Бальмера верно описывалась релятивистским волновым уравнением; уравнение формально содержало также тонкую структуру Зоммерфельда, правда, с загадочными «полуцелыми радиальными и азимутальными квантами», которые лишь позднее были объяснены в терминах спина электрона. К тому же определенные трудности возникли при попытке описать атом водорода в рамках матричной механики Гейзенберга. Корректный расчет для атома водорода осуществил Вольфганг Паули в самом конце 1925 г., но Шредингер еще не знал об этом.

Мы видим, что имелись кое-какие указания на верность релятивистского подхода. Однако всего через несколько дней Шредингер решил пожертвовать им, чтобы добиться максимального согласия с экспериментом. Он забрал рукопись из редакции и взялся за детальную разработку нерелятивистского приближения. С точки зрения математики оба подхода во многом сходны между собой, поэтому переработать рукопись не составило большого труда. Во всяком случае, 26 января 1926 г. окончательный вариант статьи был сдан в набор, а через несколько недель она появилась в «Annalen der Physik» под заголовком «Квантование как задача о собственных значениях (сообщение первое)» и стала прологом к серии работ, опубликованных Шредингером в первой половине 1926 г. и излагавших совершенно новый подход к решению актуальных проблем квантовой физики. Автор же их немедленно оказался в авангарде теоретиков квантовой механики. Центральное место в первой статье занимает выведенное на основе оптико-механической аналогии «волновое уравнение» материи, которое в своей первоначальной форме (для атома водорода) имеет вид

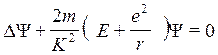, где y  — волновая функция, m — масса электрона, е — элементарный заряд, г — расстояние между электроном и ядром, Е — энергия, K=h/2n, h — постоянная Планка.