Исследование резонанса напряжений и токов в электрических цепях. Режим электрической цепи при последовательном соединении участков с индуктивностью и емкостью

Лабораторная работа № 13

Исследование резонанса напряжений и токов в электрических цепях.

Цель работы: исследовать характеристики последовательного и параллельного колебательного контура при изменении частоты источника питания.

Приборы и оборудование: персональный компьютер, прикладная программа Electronics Workbench.

Краткие теоретические сведения:

Резонанс напряжений.

Резонанс напряжений возникает при определенной для данной цепи частоте источника энергии, которую называют резонансной частотой ω_Р. При резонансной частоте.

Режим электрической цепи при последовательном соединении участков с индуктивностью и емкостью, характеризующийся равенством индуктивного и емкостного сопротивлений, называют резонансом напряжений.

Резонанс напряжений рассмотрим на схеме  идеализированной цепи (рис. 1), в которой последовательно с резистором включены идеальная катушка (без потерь) и конденсатор.

Реактивные сопротивления Х_L и X_C зависят от частоты вынужденных колебаний ω:

,     .

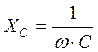Приравнивая реактивные сопротивления и учитывая, что , получим

.

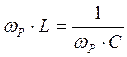Отсюда резонансная частота ,  .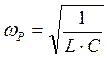

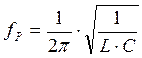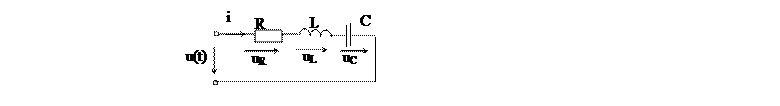
Рис. 1. Схема последовательного колебательного контура.

Резонанс напряжений в цепи можно установить двумя путями:

1)  изменением параметров L и C при постоянной частоте источника,

2)  изменением частоты источника энергии при постоянных L и C.

В связи с этим большой практический интерес представляют зависимости напряжений и токов на отдельных элементах цепи от частоты. Эти зависимости называют резонансными кривыми.

Реактивные сопротивления с изменением частоты изменяются, как показано на рис. 2,а. При увеличении частоты Х_L увеличивается пропорционально частоте, а X_C уменьшается по закону обратной пропорциональности.

Соответственно полное сопротивление  Z цепи при резонансной частоте ω_Р оказывается наименьшим, равным активному сопротивлению R; при частоте  полное сопротивление  Z увеличивается с уменьшением частоты за счет роста X_C; при частоте  полное сопротивление  Z увеличивается с увеличением частоты за счет роста X_L.

Такая зависимость полного сопротивления  Z от частоты определяет характер изменения тока при постоянном напряжении в цепи (рис 2,б). При ток равен нулю, далее с увеличением частоты ток увеличивается и при   достигает максимума I_P. Дальнейшее увеличение частоты ведет к постепенному уменьшению тока до нуля при . Аналогично изменяется напряжение на активном сопротивлении U_R, которое пропорционально току: .

Напряжение на конденсаторе U_C при равно напряжению на зажимах источника U, так как сопротивление конденсатора , что соответствует разрыву цепи на его зажимах. С ростом частоты U_C увеличивается, достигая наибольшей величины при частоте, несколько меньшей резонансной, а далее уменьшается до нуля при .

Индуктивное напряжение U_L=0 при частоте  , так как сопротивление X_L=0. Увеличение частоты ведет к увеличению U_L, которое при частоте, несколько большей резонансной, достигает максимума, а затем уменьшается до величины напряжения источника при , когда сопротивление , что соответствует разрыву цепи на зажимах катушки.

При частотах, меньших резонансных, реактивное сопротивление цепи имеет емкостной характер (отрицательно), поэтому и угол сдвига фаз в цепи отрицательный. Уменьшаясь с ростом частоты, он становится равным нулю при резонансе (), а затем меняет знак и увеличивается.

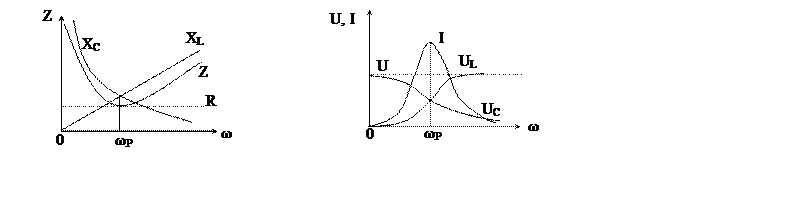
Рис. 2. Резонансные кривые.

В радиотехнике качество резонансного контура считается тем выше, чем больше отношение , называемое добротностью контура: .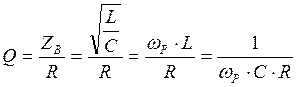

Чем меньше мощность потерь энергии в контуре (чем меньше R), тем больше добротность контура.

Большей добротности соответствует больший ток I_P при резонансе и более острая резонансная кривая. На рис. 3 показаны две резонансные кривые тока, построенные в относительных единицах при двух величинах добротности.

Все рассуждения о резонансе напряжений в идеализированной цепи можно распространить и на цепи, содержащие последовательно соединенные катушку и конденсатор с потерями. Активное сопротивление катушки и конденсатора можно рассматривать как часть общего активного сопротивления цепи R.

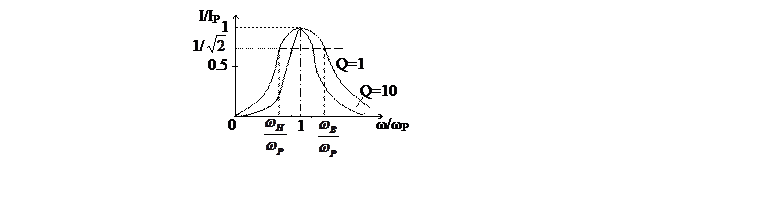
Рис. 3. Резонансные кривые при двух значениях добротности.

Резонанс токов.

Так же как и резонанс напряжений, резонанс токов возникает, когда частота источника энергии равна резонансной частоте ω_Р, а B_L=B_C.

Режим электрической цепи при параллельном соединении участков с индуктивностью и емкостью, характеризующийся равенством индуктивной и емкостной проводимостей, называют резонансом токов.

Сначала рассмотрим этот режим для схемы идеализированной цепи (рис. 4). В этой схеме параллельно резистору R включены идеальные катушка L и конденсатор C, потери энергии в которых не учитываются.

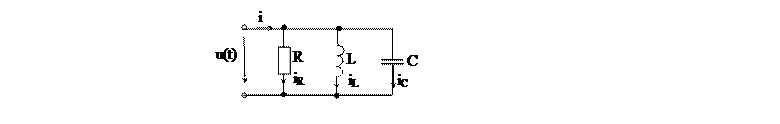
Рис. 4. Схема параллельного колебательного контура.

Реактивные проводимости зависят от частоты вынужденных колебаний.

Для рассматриваемой схемы активная проводимость 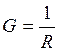, реактивные проводимости   ,   .

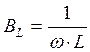При резонансе токов ;  ;  .

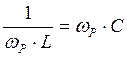Отсюда определяют резонансную частоту .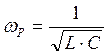

Выражение для резонансной частоты в данном случае такое же, какое было получено при рассмотрении резонанса напряжений. Резонанс токов, так же как и резонанс напряжений, можно получить изменением параметров L и C или изменением частоты источника.

На рис. 5,а показаны зависимости проводимостей от частоты. Полная проводимость цепи Y при резонансной частоте ω_Р оказывается наименьшей, равной активной проводимости G. При изменении частоты в обе стороны от резонансной полная проводимость увеличивается.

При заданном напряжении источника ток в цепи пропорционален проводимости

(рис. 5,б): , поэтому кривая I(ω) по форме повторяет кривую Y(ω). Состояние резонанса токов характеризуется наименьшей величиной тока в цепи и равенством нулю угла сдвига фаз между напряжением и током ().

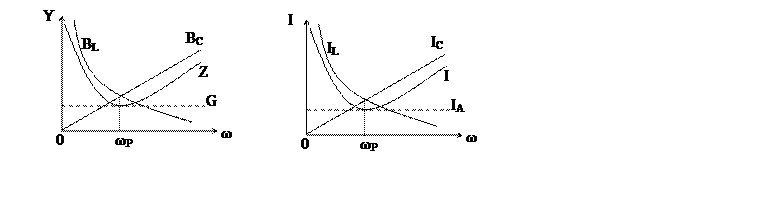
Рис. 5. Резонансные кривые.

При резонансе токов отношение тока индуктивного или емкостного элемента в неразветвленной части цепи равно отношению волновой проводимости 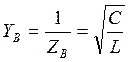 к активной проводимости цепи G.