Двухскоростная модель DDM и CAPM для оценки стоимости некотируемых активов. Стохастический аналог двухскоростной модели DDM постоянного роста

модели проблема сходимости дисконтированного ряда чистого дохода и соответственно корректности модели не возникает. Ставка дисконта в этом случае в рамках модели CAPM будет переменной величиной, зависящей от номера периода.

Ранее отмечалось, что поскольку модель CAPM является одношаговой, то она не может учитывать возможную зависимость или самокоррелированность случайной последовательности темпов изменения дохода или, соответственно, стоимости актива. Этот эффект можно оценить в рамках логнормальной модели Блэка-Шоулза, предполагая дополнительно, что темпы изменения представляют собой стационарную (в широком смысле) гауссовскую последовательность. Точнее, предполагается “логгауссовость” последовательности темпов, поскольку гауссовской предполагается последовательность логарифмов от соответствующих скоростей изменения плюс единица. В этих условиях удается получить корректировки к ранее полученным формулам для ставки дисконта с учетом возможной самокоррелиррованности последовательностей темпов (скоростей) изменения чистого дохода и стоимости замещения.

19.1. Стохастический аналог двухскоростной модели DDM постоянного роста

Будем определять случайную оценку инвестиционной цены актива из уравнения дисконтирования

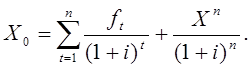    (19.1)                                                                                                                                

Здесь n –– длительность холдингового периода;

текущая оценка инвестиционной цены актива на начальный момент;

текущий чистый доход (для оценки бизнеса –– денежный поток);

i––подходящая ставка дисконта;

постпрогнозная обменнная цена актива.

Предположим, что неизвестная в силу отсутствия котировок  обменная цена актива совпадает с ценой замещения, которая оценивается в рамках затратного подхода.

Будем считать, что

где последовательности скоростей изменения дохода и стоимости, которые предполагаются независимыми одинаково распределенными случайными величинами (с.в.) со средними значениями

В силу сделанных предположений справедливы формулы для текущего дохода и цены актива:

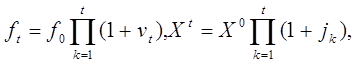      (19.2)                                                

где начальные значения чистого дохода и затратной цены, которые предполагаются известными и неслучайными. В силу независимости последовательностей среднее значение с.в.  будет равно:

        (19.3)                                                                                                                              

Вместе с (19.1) уравнения (19.3) дают детерминированную двухскоростную модель DDM постоянного роста для средних цен которые интерпретируются в модели как текущая инвестиционная стоимость актива:

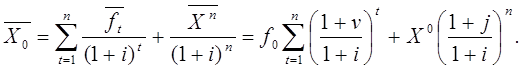      (19.4)                 

Эта модель изучалась нами в главе 16. Ставка дисконта i считалась внешним параметром модели. В настоящей работе упор делается на определение ставки дисконта. Рисковую ставку дисконта в двухскоростной модели DDM на каждом шаге можно определить в рамках модели CAPM подобно тому, как это было сделано в предыдущей главе применительно к односкоростной модели. Приведем соответствующие выкладки.                                              

19.2. Модель CAPM для определения неизвестной ставки дисконта

Имея случайную оценку (2) для чистого дохода и цены актива можно подсчитать его доходность по формуле:

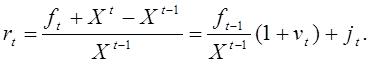                  (19.5)                                     

Мы видим, что доходность связана с темпом изменения дохода и стоимости линейной зависимостью как случайная величина. Это обстоятельство позволит нам в дальнейшем свести оценку беты актива к вычислению ковариаций темпов изменения дохода и стоимости к доходности рыночного портфеля.

Условное математическое ожидание доходности (19.5) при условии, что фиксированы, равно

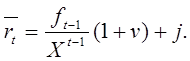                         (19.6)                                                           

С другой стороны, по модели CAPM примененной к периоду t, условная средняя доходность должна быть связана с доходностью рыночного портфеля r уравнением

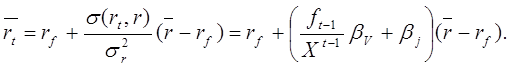    (19.7)                     

Здесь ковариация с.в.

дисперсия

средняя доходность рыночного портфеля;

безрисковая ставка дохода.

Коэффициенты бета скорости изменения дохода и стоимости определяются формулами

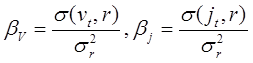.            (19.8)

В общем случае зависит от t. Однако мы будем опускать верхний индекс для простоты обозначений. Все дальнейшие выкладки остаются справедливыми и в общем случае для стационарных (в узком смысле) последовательностей  (например, последовательности независимых одинаково распределенных с.в.), что и предполагается далее. В этом случае, в частности, величины (19.8) не зависят от t.

Сравнивая два выражения (19.6) и (19.7) полученных для средней доходности актива, приходим к уравнению:

         

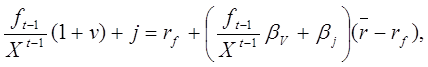
которое выполняется почти наверное (п.н.). Умножая обе части на получим уравнение

которое выполняется п.н. Беря от обеих частей математическое ожидание с учетом постоянства и формулы (19.3), получим равенство

Деля последнее равенство на  и используя (19.3), получим отсюда:

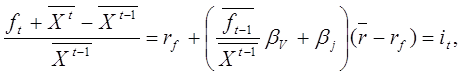
где  и будет искомой ставкой дисконтирования, как будет показано дальше. Действительно, последнее уравнение можно записать в виде:

         

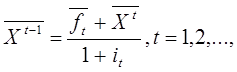
что влечет

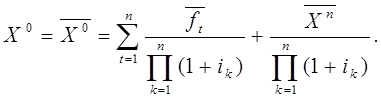          (19.9)   

Полученное равенство выражает тождество, поскольку ставка дисконтирования зависит от :

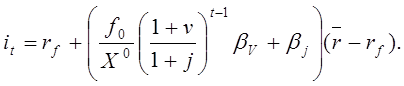               (19.10)                      

Левая часть формулы (19.9) по смыслу выражает собой текущую обменную стоимость, а правая –– текущую инвестиционную стоимость актива. При замене неизвестной стоимости в обмене стоимостью замещения тождество может нарушаться, однако его правая часть все равно может служить оценкой текущей инвестиционной стоимости актива:

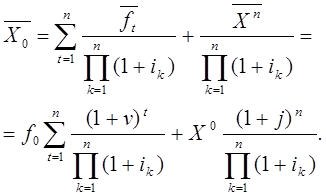               (19.11)                                    

Сравнивая (19.11) с (19.4) убеждаемся, что , выраженное формулой (19.9), действительно представляет собой подходящую ставку дисконта. Некоторая разница формул (19.11) и (19.4) объясняется тем, что полученная ставка дисконта оказалась переменной и зависит от номера периода. При этом (19.11) превращается в (19.4) при то есть (19.4) –– это частный случай (19.11).

19.3. Корректировка ставки на дополнительные риски, присущие активу

До сих пор предполагалось, что процессы являются последовательностями независимых одинаково распределенных с.в.  На практике они могут быть зависимыми. Эффект зависимости не может быть учтен в модели CAPM, поскольку последняя является одношаговой. Поэтому учет зависимости последовательности темпов (скоростей) изменения дохода означает учет дополнительных рисков, присущих активу.

Следуя модели Блэка-Шоулза (см. гл.16), предположим дополнительно логнормальность последовательностей , т.е. нормальность логарифмов

  

со средними значениями  и среднеквадратическим отклонением , что будет обозначаться в виде:

       (19.12)                                                                          

Заметим, что

 

при малых  и в этом случае характеристики с.в. также будут принимать близкие значения.

В силу сделанных предположений справедливы представления:

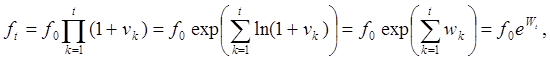 (19.13)     

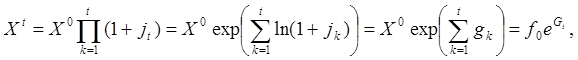 (19.14)

где обозначено для краткости

         

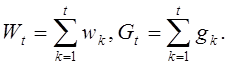
Предположим, дополнительно, что последовательности являются гауссовскими. Это означает, что для любого t наборы образует нормально распределенные векторы с неотрицательно определенными матрицами ковариаций  Известно, что набор является гауссовским тогда и только тогда, когда любая линейная комбинация элементов является нормально распределенной с.в. Кроме этого понятие независимости равносильно понятию некоррелированности для гауссовской последовательности. Исходные последовательности  естественно теперь назвать логгауссовскими по аналогии