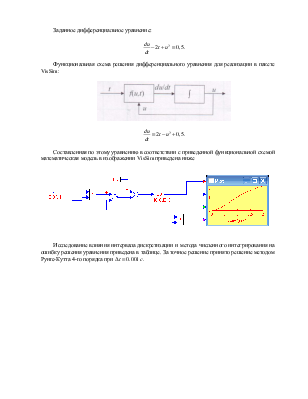
Заданное дифференциальное уравнение:
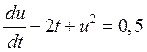 .
.
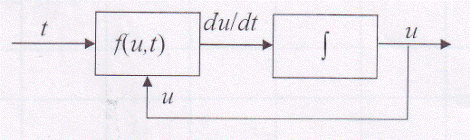
Функциональная схема решения дифференциального уравнения для реализации в пакете VisSim:
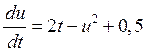 .
.
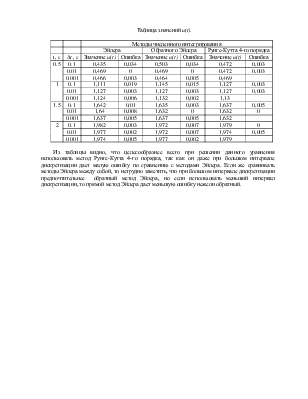
Составленная по этому уравнению в соответствии с приведенной функциональной схемой математическая модель в изображении VisSim приведена ниже
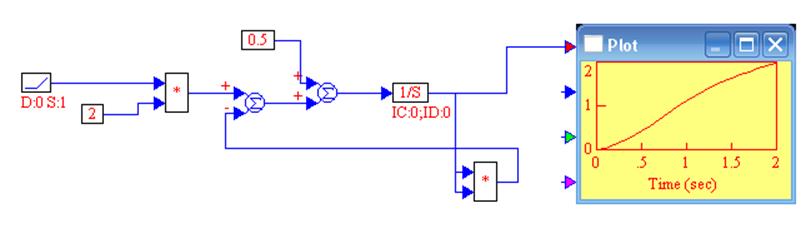
Исследование влияния интервала дискретизации и метода численного
интегрирования на ошибку решения уравнения приведена в таблице. За точное
решение принято решение методом Рунге-Кутта 4-го порядка при ![]() .
.
Таблица значений u(t).
|
Методы численного интегрирования |
|||||||
|
Эйлера |
Обратного Эйлера |
Рунге-Кутта 4-го порядка |
|||||
|
t, c |
|
Значение u(t) |
Ошибка |
Значение u(t) |
Ошибка |
Значение u(t) |
Ошибка |
|
0.5 |
0.1 |
0,435 |
0,034 |
0,503 |
0,034 |
0,472 |
0,003 |
|
0.01 |
0,469 |
0 |
0,469 |
0 |
0,472 |
0,003 |
|
|
0.001 |
0,466 |
0,003 |
0,464 |
0,005 |
0,469 |
||
|
1 |
0.1 |
1,111 |
0,019 |
1,145 |
0,015 |
1,127 |
0,003 |
|
0.01 |
1,127 |
0,003 |
1,127 |
0,003 |
1,127 |
0,003 |
|
|
0.001 |
1,124 |
0,006 |
1,132 |
0,002 |
1,13 |
||
|
1.5 |
0.1 |
1,642 |
0,01 |
1,635 |
0,003 |
1,637 |
0,005 |
|
0.01 |
1,64 |
0,008 |
1,632 |
0 |
1,632 |
0 |
|
|
0.001 |
1,637 |
0,005 |
1,637 |
0,005 |
1,632 |
||
|
2 |
0.1 |
1,982 |
0,003 |
1,972 |
0,007 |
1,979 |
0 |
|
0.01 |
1,977 |
0,002 |
1,972 |
0,007 |
1,974 |
0,005 |
|
|
0.001 |
1,974 |
0,005 |
1,977 |
0,002 |
1,979 |
||
Из таблицы видно, что целесообразнее всего при решении данного уравнения использовать метод Рунге-Кутта 4-го порядка, так как он даже при большом интервале дискретизации дает малую ошибку по сравнению с методами Эйлера. Если же сравнивать методы Эйлера между собой, то нетрудно заметить, что при большом интервале дискретизации предпочтительнее обратный метод Эйлера, но если использовать меньший интервал дискретизации, то прямой метод Эйлера дает меньшую ошибку нежели обратный.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.