Расчёт элементов конструкций. Расчёт швов. Заклёпочно-болтовые соединения, страница 3

                                                                                    (7.35)

подставив выражение 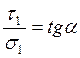 получим:

                                                                       (7.36)

Введя обозначение  и подставив в последние выражение получим:

                                                                        (7.37)

решая это уравнение совместно с

 

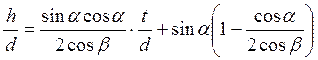
(7.38)

таким образом, используя 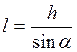 получим

                                                            

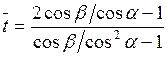
(7.39) выражая косинусы угла через тангенсы

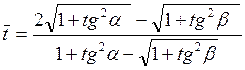                                                                     (7.40)

учитывая, что  и

 

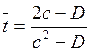(7.41)

                    где ;                                                                                            (7.42)

это выражение можно представить в виде:

                                                  (7.43)

                                                  (7.44)

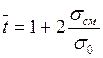
или же введя в это выражения                                                          (7.45)

                                                                                                                       (7.46)    

                                              

(7.47)

2 случай. Выполнив аналогичные выкладки как и для 1-го случая получим

                                                                                         (7.48)

                                                                                             (7.49)

8. Расчет заклепочного шва, соединяющего стенку с поясом балки

Стенки балки работают на сдвиг от перерезывающей силы Q  и при этом не теряют устойчивости.

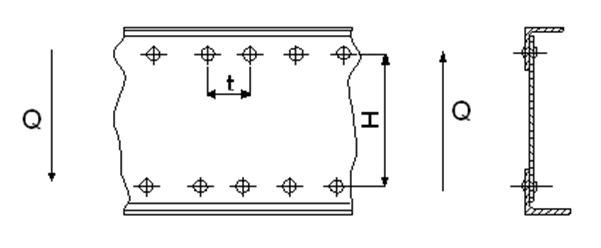
                       Рис. 8.1 Перерезывающая сила Q, действующая на стенки

Полагаем, что напряжения сдвига постоянны и равны

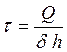                (8.1)

где  δ- толщина стенок

h- высота стенок шаг заклепок можно определить из формулы

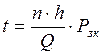                                                              (8.2)

n- число плотностей срез

Р_зк- разрушающая сила заклепок на срез

Диаметр заклепки может быть определен из условия равнопрочности заклепок на срез и стенок на смятие по формуле

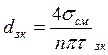                                                                                                                         (8.3)

Полученный диаметр округляется до ближайшей стандартной величины но не менее 3 мм

При двухрядном шве шаг заклепок определяется по следующему выражению:

 

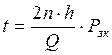(8.2)

При условии потери устойчивости стенок:

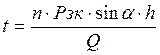                                            при однорядном шве и  (8.3)

 

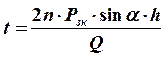при двухрядном шве   (8.4)

Здесь α- угол чисто диагонального поля распоряжений.

Можно принять α = 45˚

Расчёт проушин.

13. Расчёт  проушин  на статическую прочность.

Расчёт проушин при симметричном нагружении.

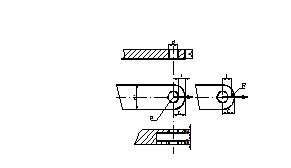
Наименьшая нагрузка, полученная  по нижеприведённым 3-м формулам считается разрушающей нагрузкой для рассчитываемой проушины.

Разрыв:                                                                                                                          (13.1)

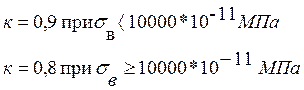     Рис. 13.1. Проушина  при  симметричном нагружении                                                                                              (13.2)

Срез:                                                  

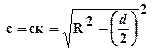    Для концентрических проушин:                                             (рис. 13.1)              (13.3)

Для неконцентрических проушин:                                                                                        

(13.4)               

где - эксцентриситет (рис. 13.1)

Смятие:                                                                                                                          (13.5)

к₁ = 1 для неподвижных разъемных соединений, к₁ = 0,5 – 0,65 для соединений неподвижных под расчетной нагрузкой, к₁ = 0,2 – 0,4 для соединений, подвижных под расчетной нагрузкой.

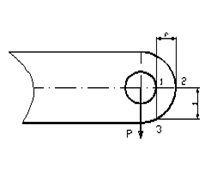Расчёт проушин, нагружённых по схеме (рис. 13.2).

Рис. 13.2 Схема нагружения проушины

Для приближенного расчёта проушин, нагруженных указанным  способом, условно считается, что разрыв происходит по удвоенному сечению 1-2, а срез по удвоенному сечению 1-3. Тогда расчетные формулы принимают вид:

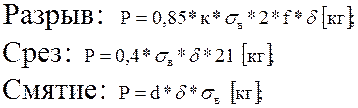                                                                                       (13.6)

Коэффициенты к₁ те же, что и в предыдущей схеме.

               Расчёт проушин  нагруженных силой и изгибающим моментом .

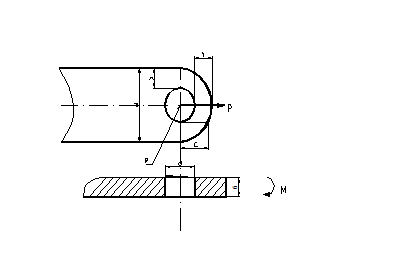Рис. 13.3 Проушина, нагруженная силой и изгибающим моментом                                         

Прочность таких проушин необходимо проверять по нормальным напряжениям.

Максимальные нормальные напряжения:

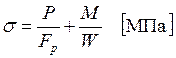                                                                                                                           (13.7)