

2.5.2. Незамкнутый контур поперечного сечения.
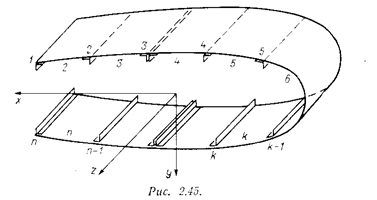 |
Соответствующие величины нормальных и погонных касательных сил на втором торцевом сечении, очевидно, будут отличаться от Рk и qk на величины приращений (dPk и dqk) этих величин по z, а так как это сечение соответствует меньшему z, чем расчётное, приращения мы берём со знаком минус.
Следует обратить внимание, что между двумя смежными рёбрами величина q постоянна по всей ширине данной панели, так как обшивку мы считаем свободной от нормальных напряжений (см. подробнее в предыдущем разделе).
Задачей расчёта на сдвиг является определение погонной касательной силы qk в любой k – й панели обшивки.
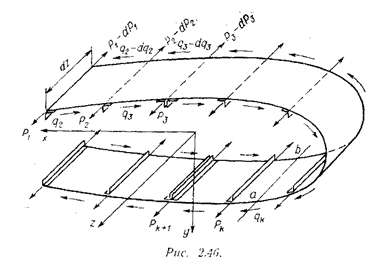
Для определения qk рассечём k – ю панель сечением по образующей (линия ab на рис. 2.46). Такое сечение разобьёт рассматриваемый нами элемент на две части. Рассмотрим условие равновесия одной из них, хотя бы верхней, приложив, разумеется, в месте разреза соответствующую погонную касательную силу q (рис. 2.47).
На рассечённой обшивке (линия ab на рис.2.47) будет действовать погонная касательная сила q, о которой из-за парности касательных напряжений известно, что в точке а она равна qk, а в точке b она равна qk - d qk. Так как расстояние между точками a и b мало (dz), будем считать, что от значения qk до значения qk - d qk погонная сила меняется линейно.
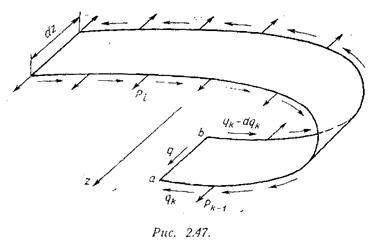
Запишем условие равновесия элемента, изображённого на рис. 2.47, спроекти-ровав все силы на ось z:
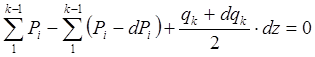 (2.33)
(2.33)
Так как член dqk dz – величина второго порядка малости, уравнение (2.33) после очевидных упрощений примет вид
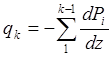 (2.34)
(2.34)
Но нормальное напряжение, а следовательно, и силы при изгибе мы уже нашли, поэтому, подставив формулу (2.34) значение Pi из расчёта на изгиб, получим погонные силы для любой (k-й) панели обшивки.
Формула (2.34) получена для открытого (незамкнутого) сечения конструкции. Обозначим погонные касательные силы для этого случая qok, т. е.
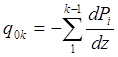 ,
(2.35)
,
(2.35)
или, меняя местами знак суммы и знак производной, (выводим производную за знак суммы), получим:
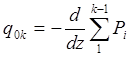 , (2.36)
, (2.36)
Подставим теперь в формулу (2.36) выражение продольных сил Рi, полученное нами при расчёте на нормальный изгиб. Мы имели:
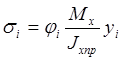 , где Jxпр – момент инерции приведенного
сечения относительно главной центральной оси х сечения;
, где Jxпр – момент инерции приведенного
сечения относительно главной центральной оси х сечения;
уi – ордината ц. т. i-го ребра;
φi – редукционный коэффициент i-го ребра;
Мх – изгибающий момент относительно оси х.
Очевидно, что
Рi = Fiσi , где Fi-площадь сечения i-го ребра с присоединённой обшивкой.
Следовательно,
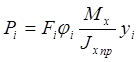 .
.
Но так как Fiφi=Fi пр, можно записать:
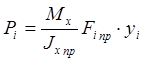 . (2.37)
. (2.37)
Подставляя (2.37) в формулу (2.36), получим:
![]() в
в ![]()
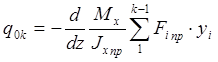 .
.
Но 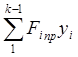 - есть статический момент относительно оси х
всех площадей редуцированного сечения рассматриваемой части конструкции.
Обозначим статический момент буквой Sxпр,
а индекс, показывающий, какие элементы входят в Sxпр,
будем ставить вверху, тогда
- есть статический момент относительно оси х
всех площадей редуцированного сечения рассматриваемой части конструкции.
Обозначим статический момент буквой Sxпр,
а индекс, показывающий, какие элементы входят в Sxпр,
будем ставить вверху, тогда
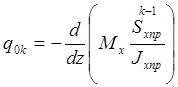 .
.
Распишем теперь производную произведения так:
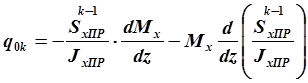 . Подставляя
. Подставляя 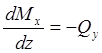 , получим
, получим
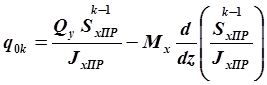 . (2.38)
. (2.38)
В формуле (2.38) все величины или уже известны, или могут быть вычислены, следовательно, могут быть найдены и погонные касательные силы во всех панелях сечения. Правда, вычисление члена
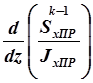
(2.39)
для каждой панели обшивки чрезвычайно трудоёмко. Очевидно, что этот член отличен от нуля только в случае переменного по длине сечения.
В практических расчётах этим членом пренебрегают и тогда формула примет очень удобный для использования вид:
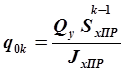
(2.40)
2.5.3. Приближённый учёт «конусности» конструкции
Отброшенный второй член правой части равенства (2.38) может быть вычислен приближённо для конструкции со слабо меняющимся по длине сечением. Для того, чтобы применить формулу (2.38) в расчёте какого-нибудь из сечений крыла z = c, нам достаточно иметь значение производной (2.39) при соответствующем z. Рассмотрим небольшой длины отсек крыла, содержащий это расчётное сечение z = c (рис. 2.48). В пределах этого отсека мы можем положить
![]() ;
;
![]() .
.
Здесь Fi пр(z) и уi(z) – текущие значения приведенных площадей сечений и ординат их центров тяжести;
Fi пр и уi – тоже для расчётного сечения;
ψ1(z) и ψ(z) – некоторые функции z/
Тогда текущие значения статического момента Sx пр и момента инерции сечения Jx пр запишутся так:
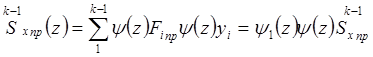 ;
;
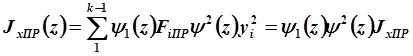
.
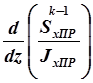
В этом случае выражение (2.39) →
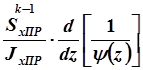 принимает более удобный для применения
вид
принимает более удобный для применения
вид
. (2.41)
В пределах малой длины отсека функцию ψ(z) допустимо считать линейной.
Пусть в точке О на оси z пересекутся мысленно продолженные нами образующие на рис. 2.48. Тогда из подобия треугольников получим
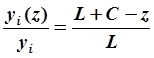 |
|||
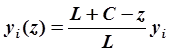 |
|||
, или .
Следовательно,
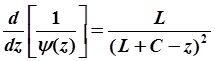
В сечении z = C эта производная примет значение
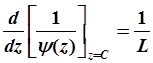 |
.
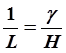 Если обозначить высоту расчётного сечения
на рис. 2.48 буквой Н, а угол между крайними образующими отсека γ,
то при малом γ
Если обозначить высоту расчётного сечения
на рис. 2.48 буквой Н, а угол между крайними образующими отсека γ,
то при малом γ
Н = γL или .
Тогда выражение (2.41) примет предельно простой вид
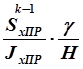 |
. (2.42)
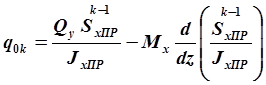
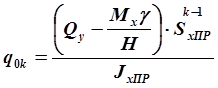 Остаётся подставить
полученное выражение для производной (2.42) в формулу (2.38)
Остаётся подставить
полученное выражение для производной (2.42) в формулу (2.38)
, получим . (2.43)
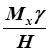 Получена , таким образом, очень простая
формула (2,43), позволяющая учитывать «конусность» крыла при расчёте на сдвиг.
Она отличается от формулы (2.40) только тем, что взамен поперечной силы в
сечении принимается уменьшенная за счёт «конусности». Величина вычисляется
в каждом сечении достаточно просто, так как Н и γ
могут быть сняты прямо с чертежа.
Получена , таким образом, очень простая
формула (2,43), позволяющая учитывать «конусность» крыла при расчёте на сдвиг.
Она отличается от формулы (2.40) только тем, что взамен поперечной силы в
сечении принимается уменьшенная за счёт «конусности». Величина вычисляется
в каждом сечении достаточно просто, так как Н и γ
могут быть сняты прямо с чертежа.
Продолжение следует!
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.