











поступим следующим образом:
выберем рабочий диапазон L0 (вводимых
концентраций пиридина) таким, чтобы выполнялось условие ![]() . Тогда можно считать, что
. Тогда можно считать, что ![]() . Оценим ∆D
для концентраций пиридина L2 и L1 соответственно. Примем также, что
концентрация L1 очень мала по сравнению с L2, т.е. L1<<L2 и ∆L≈L2.
. Оценим ∆D
для концентраций пиридина L2 и L1 соответственно. Примем также, что
концентрация L1 очень мала по сравнению с L2, т.е. L1<<L2 и ∆L≈L2.
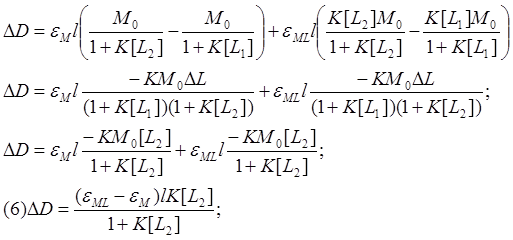
Уравнение (6) даёт
зависимость изменения оптической плотности при изменении концентрации лиганда.
Зависимость имеет довольно сложный характер, поэтому работать с ней неудобно.
Этот недостаток можно ликвидировать за счёт анализа обратной зависимости: 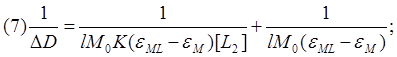
Таким образом, итогом преобразований является зависимость типа (7), имеющая линейный характер. Последовательно сняв и проанализировав спектры для ряда концентраций пиридина, мы получили набор экспериментальных точек, позволяющих определить константу равновесия K графически.
Концентрацию пиридина
в исследуемом растворе определяли следующим образом. Для реакции брали пиридин
с плотностью 0,978 г/см3, молярная масса 79,10 г/моль,
следовательно, концентрация пиридина в чистом пиридине равна: 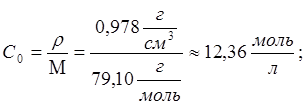 При добавлении некоторого объёма пиридина
возникает поправочный коэффициент разбавления – уменьшается концентрация
пиридина в
При добавлении некоторого объёма пиридина
возникает поправочный коэффициент разбавления – уменьшается концентрация
пиридина в 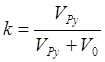 раз. Одновременно уменьшается
концентрация M0.в
раз. Одновременно уменьшается
концентрация M0.в 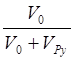 раз.
Последнее обстоятельство приводит к накоплению ошибки по мере увеличения
добавленного объёма пиридина.
раз.
Последнее обстоятельство приводит к накоплению ошибки по мере увеличения
добавленного объёма пиридина.
Определение ∆rG0.
Следующая задача
нашей работы состояла в оценке зависимости константы равновесия от температуры.
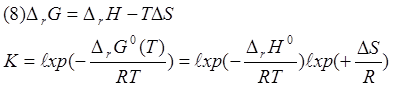 Нами были проведено определение константы
равновесия при трёх температурах: 21; 30; 45°С.
Сравнивая полученные значения, мы смогли сделать вывод, что константа
равновесия убывает с ростом температуры, откуда следует ∆rG0<0.
Нами были проведено определение константы
равновесия при трёх температурах: 21; 30; 45°С.
Сравнивая полученные значения, мы смогли сделать вывод, что константа
равновесия убывает с ростом температуры, откуда следует ∆rG0<0.
В принципе, возможны четыре ситуации, которые можно описать таблицей (таблица 1).
Таблица 1
|
Значение ∆rG0 |
K(T) |
Температура |
|
положительно |
возрастает |
возрастает |
|
убывает |
убывает |
|
|
отрицательно |
возрастает |
убывает |
|
убывает |
возрастает |
Воспользуемся
формулой (8) для приблизительной оценки энтропии. Зависимость ∆rG0 от температуры в первую очередь
определяется вкладом энтропии. Поэтому для оценки примем, что энтальпия и
энтропия реакции являются постоянными величинами в данном интервале температур
(25 К). Тогда можно решить систему
уравнений для двух измерений: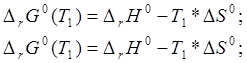 Тем не менее,
сравнить значения ∆S0 можно только между собой, оценивая
сходимость результатов. Теоретически рассчитать или оценить изменение энтропии
даже в данной простой реакции нам представляется довольно затруднительным.
Тем не менее,
сравнить значения ∆S0 можно только между собой, оценивая
сходимость результатов. Теоретически рассчитать или оценить изменение энтропии
даже в данной простой реакции нам представляется довольно затруднительным.
Формулы метода наименьших квадратов, использованные в работе:
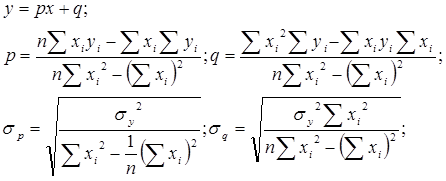
Для работы использовали следующие реактивы: ацетилацетонатный комплекс ванадила VO(acac)2 (молярная масса 267,1748 г/моль), пиридин C5H5N (молярная масса 79,10 г/моль, плотность 0,978 г/см3). В качестве растворителя был выбран высушенный от воды хлороформ CHCl3 (молярная масса 119,38 г/моль, плотность 1,492 г/см3).
1. На аналитических весах взвешено необходимое количество исходного комплекса. Масса навески 0,0526г (0,007456 моль). Навеску поместили в мерную колбу на 50мл, довели до метки растворителем. Получен раствор с теоретической концентрацией M0=0,007875 М.
2. Для регистрации спектра поглощения посредством спектрометра SPECORD приготовили 2 кюветы. В одну был налит чистый растворитель (хлороформ, 3мл) – раствор сравнения, в другую – такое же количество раствора исходного комплекса. Сняли спектр чистого соединения VO(acac)2.
3. В кювету с раствором комплекса последовательно вводили с помощью
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.