Контрольная работа по курсу "Физика". Вариант № 10

определения количества теплоты, выделившейся за время t, данное выражение следует проинтегрировать в пределах от 0 до t;

 

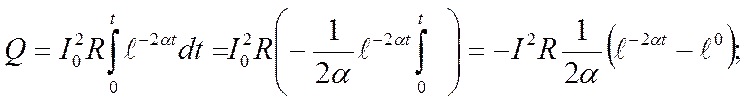
Отдельно вычисляем 2αt:

2αt = 2*10с^-1*1с = 20

Тогда

Воспользуемся правилами приближенного вычисления:

Тогда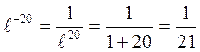

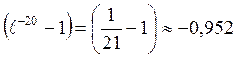
Вычисляем Q:

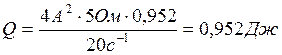
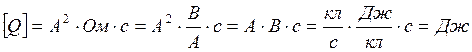
Ответ: Q=0,952Дж

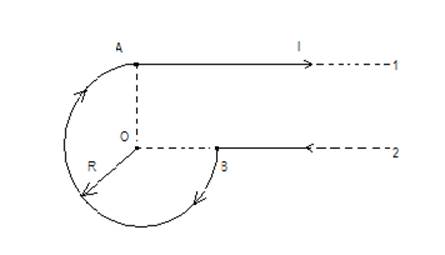
220.Найти индукцию магнитного поля, создаваемого бесконечным длинным проводником с током I, изогнутым так, как показано на рис.28 (в – для 220)

Рисунок к задаче

(Рис.1)

Магнитное поле в точке О создано прямым токам в проводнике 1 и круговым токам по дуге АВ. Проводник 2 в точке О не создает магнитное поле,(его продолжение проходит через точку О).

Согласно принципу суперпозиции индукция магнитного поля в точке О равно геометрической сумме

где B₁ – магнитная индукция поля, созданного бесконечно длинным проводником 1 и определяется по формуле

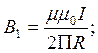
Для определения магнитной индукции поля, созданного круговым током используем закон Био-Савара-Лапласа.

(рис.2)

Выбирая элемент проводника ∆ℓ₁ малым, можно считать его прямолинейным и перпендикулярным к прямой, соединяющей его с центром окружности (рис. 2). При этом условии угол α равен 90°. Получаем:

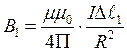
Аналогичные выражения определяют индукцию магнитного поля, создаваемого в центре окружности другими   элементами   проводника:  ∆ℓ₂,∆ℓ₃,... ∆ℓ_n  Индукцию магнитного поля В, создаваемого всем круговым током, можно найти суммированием векторов индукции отдельных элементов проводника с током ∆ℓ₁,∆ℓ₂,… ∆ℓ_n. Все эти векторы параллельны, поэтому модуль вектора индукции кругового тока определяется выражением:     

;

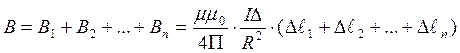Где (∆ℓ₁,∆ℓ₂,… ∆ℓ_n)=, где L=2ПR – длинна всей окружности.

Тогда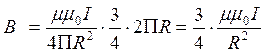

Множитель  указывает на то, что дуга составляет части от длины кольца с центром О. (из рисунка видно)

Для определения направления векторов  и  применяем правило буравчика (или правой руки). Вектора  и  параллельны и направлены от нас.

Словно, модуль магнитной индукции В в точке О равен алгебраической сумме модулей  и ;

 или

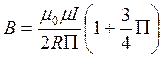 где

μ=1 – магнитная проницаемость среды (воздух),

 - магнитная постоянность,

I – сила тока в проводнике,

R – расстояние (радиус) до точки О;

 

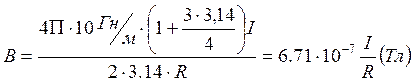
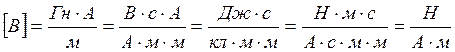
Ответ: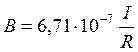

230. Плоский контур с током I= 50 А расположен в однородном магнитном поле (B= 0,6 Тл) так, что нормаль к контуру перпендикулярна линиям магнитной индукции. Определить работу, совершаемую силами поля при медленном повороте контура около оси, лежащей в плоскости контура, на угол &3945;= 30⁰.

 

Дано                                          Решение

I = 50А              На контур с током в магнитном поле действует вращающий момент

B = 0,6Тл           рм В sinφ                           (1)

α = 30⁰                    где рм – магнитный момент контуры,

                          В – индукция магнитного роля,

А - ?               φ – угол между векторам м, направленным по нормам к контуру и вектором .

По условию задачи в начальном положении контур находился параллельно вектору , следовательно, м и sin90⁰ = 1.

При этом момент сил М равен максимальному значению М_мах = рм В Так как момент сил переменный (зависит от угла поворота φ), то для подсчёта работы применим формулу работы в

 

с учётом выражения (1) и учётом что

где S – площадь контура с током I, получаем

                                  (2)

По условию задачи, контур поворачивался на угол α = 30⁰ около оси, летающей в плоскости контура.

Сл-но угол φ после поворота будет равен

φ = 90 – α = 60⁰

Взяв интеграл от выражения (2), находим работу, совершаемую силами поля при медленном повороте контура на угол φ:

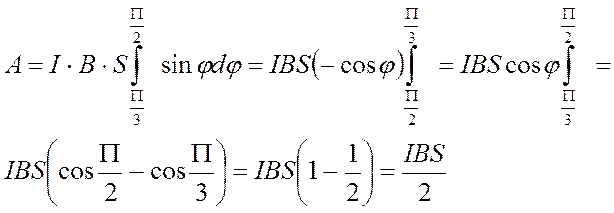
(В условии задачи не указаны размеры контура, поэтому ответ можно оставить в общем виде для любого контура с током I, помещённого в магнитное поле с индукцией В).

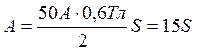 (Тл)

Ответ: А=15S(Тл)

240.В вакууме распространяются две плоские электромагнитные волны; одна – вдоль оси X, другая – вдоль оси Y:

® E 1  = ® E 0  cos(wt - kx), ® E 2  = ® E 0  cos(wt - ky),

где вектор

® E 0

направлен параллельно оси Z. Найти среднее значение плотности потока энергии в точках плоскости Y=X.

Дано

® E	1	=	® E	0	cos(wt - kx),
® E	2	=	® E	0	cos(wt - ky),

 - ?                                                  Решение

Плотность потока энергии ј определиться как энергия w, переносимая излучениям в единицу времени через единицу площади.

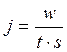        (1)

Где w –энергия заключённая в пространстве объёмам V.

w выражается через объёмную плотность энергии ω формулой

w=ωV

Объём V=SCt, где C- скорость э/м волны

Зная что ω=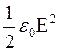 преобразуем (1)

j=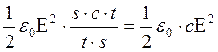,      (2)

Где  - электрическая постоянная, Е – модуль напряжённости электрического поля.

По условию задачи две волны э/м поля распространяются по двум взаимно перпендикулярным направлениям. Следовательно, напряжённость в точках плоскости  (т.е х = у) выражается векторной суммой   и , т.е 

Модуль напряжённости Е определяется по теореме Пифагора

с учётом что х = у;

Применим формулу для понижения степени

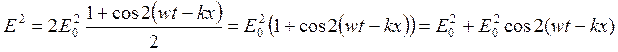
Первая составляющая напряжённости  не зависит от времени и представляет собой постоянную часть мгновенного значения напряжённости за сколь угодно длительный промежуток времени. Вторая составляющая – переменная –есть функция косинуса удвоенного угла и её среднее значение за период колебаний равно 0 (за  все значения cos<0, все значения cos>0)

Таким образам, среднее значение напряжённости эл. поля за длительный промежуток времени определяется по формуле.

Тогда преобразуем (2)

j,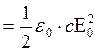

Ответ: j,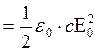

250. Установка для наблюдения колец Ньютона освещается нормально падающим монохроматическим светом (λ = 590 нм). Радиус кривизны R линзы равен 5 см. Определить толщину d₃ воздушного промежутка в том месте, где в отраженном свете наблюдается третье светлое кольцо.

 

Дано

λ = 590 нм = 590                   

R = 5см = 5

m = 3

 

d₃ - ?

Решение

Рисунок задаче:

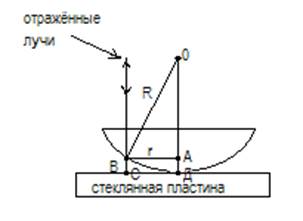
Волны отражённые от поверхности линзы в точке В и от поверхности пластины в точке С имеют разность хода 2ВД. Отрезок ВД равен толщине воздушного зазора d₃  в том месте, где в отражённом свете наблюдается третье светлое кольцо, т.е ВД = d₃.

При отражении от поверхности пластины в точке А происходит