Шкала скидок оптовых продаж по одному товару методом постоянного маржинального дохода

Министерство образования Республики Беларусь

Учреждение образования

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Контрольная работа

по курсу

"Оптимизация маркетинговых решений "

                                                                  .

                                                            группа №702221, шифр №21

                                                             

                                                                             е-мейл

Содержание

1.  Методы прогнозирования покупательского спроса

2.  Методы оценки конкурентоспособности товаров

3.  Определить шкалу скидок оптовых продаж по одному товару методом постоянного маржинального дохода.

4.  Определить коэффициенты важности потребительских свойств товара методом парных сравнений.

Литература

1. Методы прогнозирования покупательского спроса.

Прогнозирование спроса (объемов продаж) в зависимости от цены или дохода выполняется с помощью моделей простой или многофакторной регрессии.

Модель простой регрессии имеет вид

y = F(x)                                                   (1.1)

где у – спрос; х – фактор, влияющий на спрос (цена или доход покупателей).

Модели регрессии строятся на основе динамических рядов рассматриваемых показателей.

Обычно при прогнозировании спроса используют следующие модели простой регрессии (табл.14.2)

     Таблица 14.2

Прогнозирование спроса с помощью моделей простой регрессии

Модель регрессии	Функция  F(x)	Производная
1. Линейная
2. Квадратичная
3. Полиномиальная
4. Гипербола
5. Полулогарифмическая
6. Показательная
7. Логистическая
8. Степенная

Выбор модели осуществляется по критерию максимума коэффициента детерминации.

Для прогнозирования коэффициента эластичности на основе модели регрессии используется следующая формула:

(1.2)

где   производная функция регрессии относительно фактора х.

Пример 1.  Для прогноза спроса и коэффициента эластичности спроса относительно дохода по данной табл. 14.1 при увеличении дохода до 1500 ден.ед.

Таблица 14.1

Решение

С помощью функции «Анализ данных» EXCEL построена модель регрессии спроса в зависимости от дохода:

Коэффициент детерминации модели равен 0,98, следовательно модель имеет высокую точность. Тогда спрос на товар при доходе 1500 ден.ед. будет равен 378 ед.

Коэффициент эластичности будет равен

На практике на спрос влияет одновременно несколько факторов. В этом случае для прогнозирования спроса обычно используются модели линейной многофакторной регрессии  вида

               (1.3)

где х₁,х₂,…, х_n – факторы, влияющие на спрос (цена, доход, продажа других товаров).

Степень влияния на каждый фактор на спрос определяется с помощью коэффициентов парной корреляции:

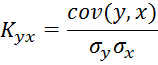
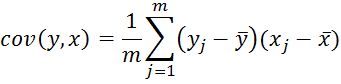
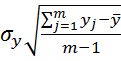(1.4)

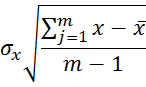
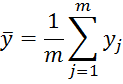
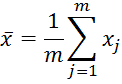
где y_j, x_j – наблюдаемые значения показателей; j – номер наблюдения; m –  количество наблюдений.

Показателем тесноты связи между показателями является модуль коэффициента парной корреляции . Чем ближе он к единице, тем теснее связь между показателями (табл.14.3). Если К_ух >0, то имеется положительная корреляция – при возрастании х в среднем у возрастает; если К_ух <0, то имеется отрицательная корреляция – при возрастании х в среднем у убывает; К_ух =0, то линейная связь отсутствует.

     Таблица 14.3

Школа тесноты связи между показателями

Показатели тесноты связи, Кух	Характеристика связи
0,1-0,3	Слабая
0,3-0,5	Ниже средней
0,5-0,7	Средняя
0,7-0,9	Высокая
0,-1,0	Сильная

При отсутствии модели надо выбирать факторы, у которых есть высокая теснота связи между показателями, т.е. .

Оценка значимости коэффициентов регрессии выполняется по t– критерию Стьюдента, оценка значимости коэффициента детерминации выполняется по F – критерию Фишера.

В случае линейной модели спроса (1.3) коэффициенты эластичности по каждому фактору определяется по формуле

                                     (1.5)

гдеi = 1, 2, …, n.

В случае применения модели нелинейной регрессии, ее сводят заменой переменных к линейной регрессии, а после определения коэффициентов линейной модели с помощью функции «Анализ данных» EXCEL снова возвращаются к нелинейной модели.

Если спрос имеет постоянную эластичность, то применяются модель

                                 (1.6)

При определении коэффициентов модели (1.6) ее сводят к линейной с помощью логарифмирования и замены переменных:

                            (1.7)

Коэффициент эластичности спроса от различных факторов в модели (1.7) будут равны

                                                (1.8)

В случае общей нелинейной модели регрессии

                                     (1.9)

Коэффициент эластичности спроса от факторов определяются по формуле

                                                    (1.10)

На основе значения  определяют, какой фактор в процентном