Природно-климатическое описание строительной площадки. Вариантное проектирование. Цех по изготовлению мебели

расположении волокон R_и=14 МПа; при поперечном расположении волокон R_и90=11,5 МПа. Модуль упругости по табл. 2 СНиП Е_а=10⁴ МПа. Для древесины ребер в соответствии с табл. 3 и пп. 3.2; 3.5 СНиП II-25-80 имеем: расчетное сопротивление изгибу R_и=13*0,95=12,35 МПа; модуль упругости Е_др=10⁴ МПа.

Проверка верхней обшивки на изгиб. Момент инерции и момент сопротивления полосы обшивки шириной b=1000 мм при толщине δ=8 мм:

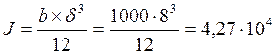 мм⁴

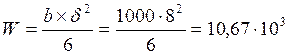 мм³

Максимальный изгибающий момент и максимальный прогиб определяют в обшивке как для трехпролетной неразрезной балке с пролетами, равными l=466 мм (рис. 5)

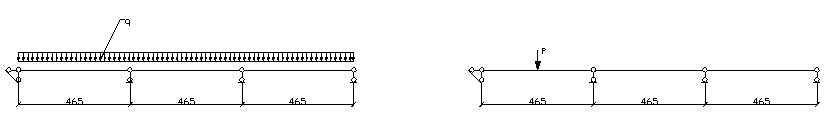
Рис. 5. Расчетная схема верхней обшивки

(равномерная нагрузка; сосредоточенный груз)

Максимальный изгибающий момент от полной равномерно распределенной нагрузки будет на второй опоре.

 кН∙м

Напряжение от изгиба:

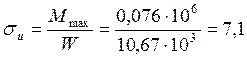 МПа < 11,5 МПа

Относительный прогиб от нормативной равномерно распределенной нагрузки максимальным будет в первом пролете обшивки:

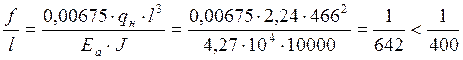
Максимальный изгибающий момент от действия сосредоточенного груза Р=1,2 кН в середине первого пролета (рис. 5):

 кН∙мм

Напряжение от изгиба:

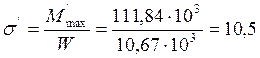 МПа < 11,5∙1,2 МПа

Расчет среднего продольного ребра. Средние ребра воспринимают большую нагрузку от трехпролетной плиты обшивки и нагрузка на 1 м среднего ребра будет составлять: нормативная q_н=1,1∙3,0∙0,466=1,54 кН/м; расчетная q=1,1∙4,36∙0,466=2,23 кН/м.Сечение средних ребер: высота h_р=210 мм, ширина b_р=67 мм. Момент сопротивления поперечного сечения:

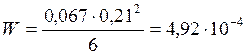 м⁴

Изгибающий момент в ребре при расчетном пролете l_р=0,99∙l=0,99∙2,98=2,95 м и расчетной нагрузке на ребро q=2,23 кН/м составляет:

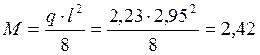 кН∙м

Напряжение от изгиба:

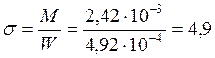 МПа < 12,35 МПа

Проверка прогиба панели. Нормативная нагрузка на 1 м панели:

 кН/м

Суммарный момент инерции поперечного сечения клееных продольных ребер панели:

 м⁴

Относительный прогиб панели:

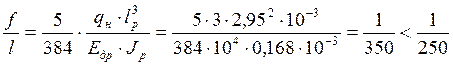, где

 - предельный прогиб в панелях покрытия согласно табл. 16 СНиП II-25-80.

6.  Расчет балки.

6.1.  Сбор нагрузок:

Нагрузки, действующие на балку сведены в таблицу:

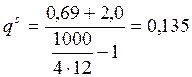 кН/м²

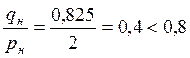
Нагрузка на 1 м балки:

q^н=2,825∙3=8,48 кН/м

q^р=4,187∙3=12,56 кН/м

6.2.  Конструкция балки.

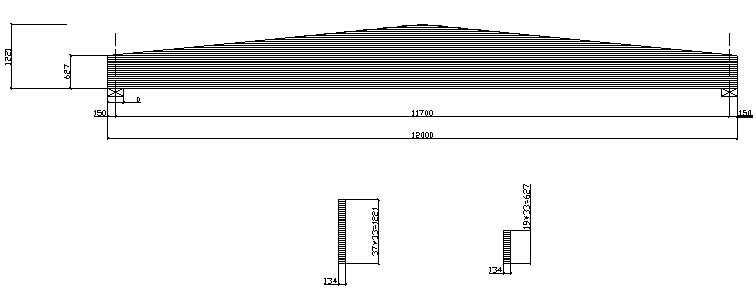
Рис. 6. Двускатная дощато-клееная балка.

Балка дощато-клееная двускатная (рис. 6). Уклон 1:10. Изготовлена из сосновых досок второго сорта, размером 150×40 мм. Доски после фрезерования будут иметь размер 134×33 мм. Высота балки в середине и на опоре должна быть кратной толщине доски, т.е. 33 мм.

Принимаем высоту балки в середине, равной примерно  мм, что составляет 37 досок, а высоту балки на опоре примерно  мм. Расчетный пролет l=11,7 м.

6.3.  Статический расчет балки.

Опорная реакция балки

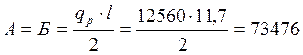 Н

Расстояние от левой опоры до сечения с наибольшими нормальными напряжениями:

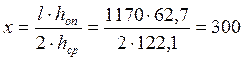 см

Момент в сечении x=300 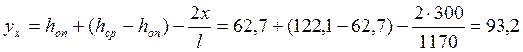см

 см.

Число целых досок n=93,2/3,3=28 шт. Расчетная высота  см. Момент сопротивления в сечении x=300 см:

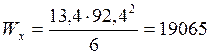 см³

Максимальное напряжение:

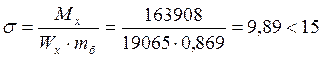 МПа

Момент инерции балки:

- в опорном сечении

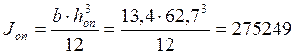 см⁴

- в среднем сечении

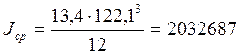 см⁴

Статический момент в опорном сечении балки:

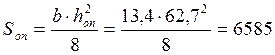 см³

Касательные напряжения в опорном сечении балки:

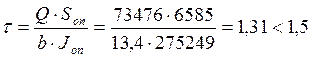 МПа

6.4.  Проверка устойчивости плоской формы деформирования.

В качестве связей применяем полураскосную систему с расстоянием между ригелями 3,0 м. Связи расположены со стороны сжатой кромки балки:

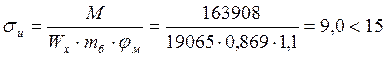 МПа, где

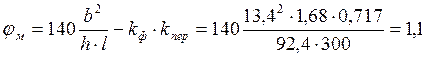
Коэффициент, зависящий от формы эпюры моментов, по эпюре 2 табл. 2 прил. 4 СНиП II-25-80 при моментах для x=4,95 м.

 Н∙м и для x=1,05 M_1,05=79128 Н∙м 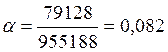; К_ф=1,75-0,75∙0,082=1,68.

Коэффициент, учитывающий переменность сечения по высоте

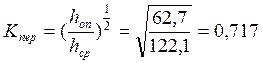
Прогиб балки определяют с учетом переменного сечения

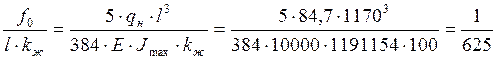
Коэффициент переменности сечения для дощато-клееной балки прямоугольного сечения:

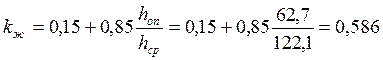
Приведенный момент инерции:

 см⁴

Полный относительный прогиб:

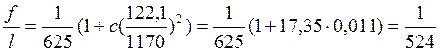, что меньше (1/300)l.

Коэффициент, учитывающий влияние деформаций сдвига от поперечной силы:

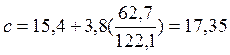
7.  Статический расчет рамы.

7.1.  Предварительный подбор сечения колонн.

Задаемся λ=120 (гибкость)

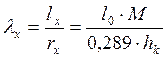
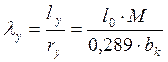
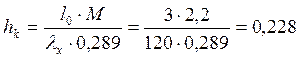
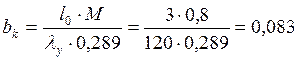
Принимаем:

h_k=19×33=297 мм

b_k=134 мм.

7.2.  Сбор нагрузок.

Расчетная схема:

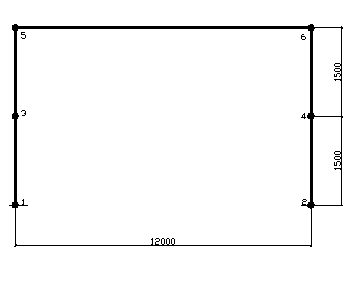
Определим жесткости колонны и балки:

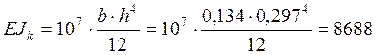 кН∙м⁴

 кН∙м²

 кН∙м⁴

 кН∙м²

Загружение 1 (снег)

 кН∙м²

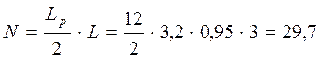кН  

Загружение 2 (ветер)

, где с=0,8 (наветренная); с=-0,6 (подветренная). к=0,75 (h<5 м).

 кН/м

 кН/м

Загружение 3 (собственный вес)

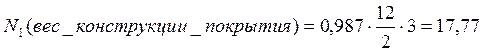 кН

 кН

 кН

 кН, где

e – эксцентриситет. 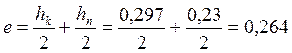 м

Расчет рамы производим по программе SCAD и результаты и эпюры усилий сводим в приложение 1.

8.  Расчет колонны.

Расчет колонны на прочность по нормальным напряжениям и по устойчивости плоской формы деформирования.

Определим расчетные (максимальные) напряжения в колонне.

 кН

 кН∙м

l₀=2,2∙H=2,2∙3=6,6 м

Площадь сечения колонны:

 м²

Момент сопротивления:

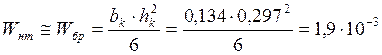 м³

Гибкость

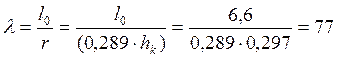
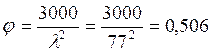
При древесине третьего сорта и при принятых размерах сечения по табл. 3 СНиП II-25-80.

 МПа

С учетом m_н, m_сл=1 и коэффициента надежности γ_n=0,95 получим:

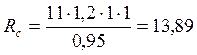 МПа

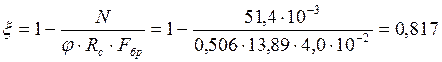
Здесь и далее при расчете на прочность и устйчивость в формулах проверки удобно значения N и Q записывать в МН, а значение М в МН м

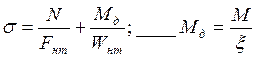
При эпюре моментов треугольного очертания (см. п. 4.17 СНиП II-25-80) поправочный коэффициент к ξ

 /СНиП II-25-80/

В данном случае эпюра момента близка к треугольной.

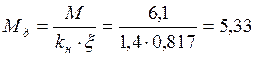 кН∙м;

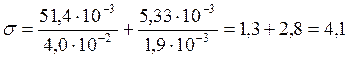 МПа < 13,89 МПа

Оставляем ранее принятое сечение, исходя из необходимости ограничения гибкости.

Расчет на устойчивость плоской формы деформирования производится по формуле (33) СНиП II-25-80. Принимаем, что распорки по наружным рядам колонн (в плоскости, параллельной наружным стенам) идут только по верху колонн. Тогда l_p=H, l₀=H.

В формуле

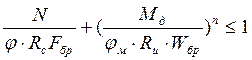
показатель степени n=2 как для элементов, не имеющих закрепления растянутой зоны из плоскости деформирования.

 МПа

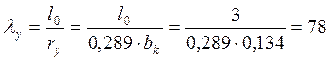
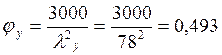
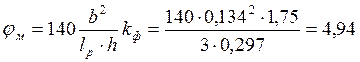
Применительно к эпюре моментов треугольного очертания (см. табл. 2, прил. 4 СНиП II-25-80):

d=0, т.к. момент в верхней части колонны равен 0:

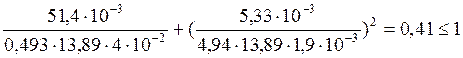
Следовательно устойчивость обеспечена.

Расчет на устойчивость из плоскости как центрально сжатого стержня. φ=0,493 (см. расчет на устойчивость плоской формы деформирования); N=52,87 (для второго сочетания нагрузок ):

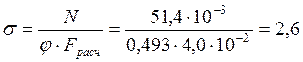 МПа  11,57 МПа, где

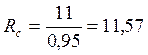   МПа

Устойчивость из плоскости обеспечена.

9.  Расчет узла защемления колонны в фундаменте.

Принимаем решение узла защемления колонны в фундаменте с применением железобетонной приставки из бетона класса В25 (R_в>R_с=R_см=13,89 МПа), из которой выпущены четыре стержня из арматуры периодического профиля из стали класса А-II (рис. 7). Вклеивание арматурных стержней древесину осуществляется с помощью