Лабораторная работа №3
ГАРМОНИЧЕСКАЯ ВИБРАЦИЯ
 Цель
работы: подвергнуть конструкцию, представленную на рис. 6 и состоящую
из пластин с разными физическими свойствами, гармоническому анализу и получить:
перемещения и ускорения на заданном интервале частот, форму колебаний на
резонансной частоте.
Цель
работы: подвергнуть конструкцию, представленную на рис. 6 и состоящую
из пластин с разными физическими свойствами, гармоническому анализу и получить:
перемещения и ускорения на заданном интервале частот, форму колебаний на
резонансной частоте.
|
Тип анализа |
Структурный |
|
Тип используемого конечного элемента |
Оболочка (Shell) |
|
Тип граничных условий |
Жесткое защемление боковой грани и равномерно распределенная нагрузка |
|
Возможности |
Получение: резонансной частоты, формы колебаний на резонансной частоте и ускорения на заданном интервале частот. |
Рис. 6
Порядок выполнения работы:
1. Определяем тип анализа:
MAIN MENU => PREFERENCES…=> STRUCTURAL=> ОК.
1. Выполняем следующую последовательность действий:
M.M. => PREFERENCES… => STRUCTURAL => OK. Таким образом, фильтруется все меню под структурный расчет.
2. Задаем свойства материалов и определяемся с типом элементов.
Выбираем тип элементов:
 M.M. => PREPROCESSSOR => ELEMENT TYPE => ADD/EDIT/DELETE
=> ADD…=> STRUCTURAL SHELL ELASTUC 4 NODE 63 => OK
=> CLOSE. Сначала определяем толщины используемых пластин, для этого: M.M. => PREPROCESSOR
=> REAL CONSTANTS => ADD/EDIT/DELETE => ADD =>
ОК и в пункте SHELL THICKNESS AT NODE I TK(I) задаем толщину пластины равную 0,006 метрам и
повторяем операцию ADD => ОК, задаем
толщину второго материала равную 0,012 метрам. Далее задаём
свойства материалов:
M.M. => PREPROCESSSOR => ELEMENT TYPE => ADD/EDIT/DELETE
=> ADD…=> STRUCTURAL SHELL ELASTUC 4 NODE 63 => OK
=> CLOSE. Сначала определяем толщины используемых пластин, для этого: M.M. => PREPROCESSOR
=> REAL CONSTANTS => ADD/EDIT/DELETE => ADD =>
ОК и в пункте SHELL THICKNESS AT NODE I TK(I) задаем толщину пластины равную 0,006 метрам и
повторяем операцию ADD => ОК, задаем
толщину второго материала равную 0,012 метрам. Далее задаём
свойства материалов:
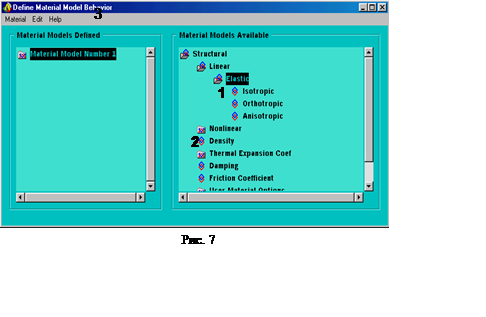
M.M. => PREPROCESSSOR => MATERIAL PROPS => MATERIAL MODELS. Затем, следуя цифрам на рис. 7, выполняем следующие действия:
А. Двойным нажатием мыши на указанные папки выполняем:
STRUCTURAL => LINEAR => ELASTIC => ISOTROPIC. В окне LINEAR ISOTROPIC PROPERTIES FOR MATERIAL NUMBER 1 задаем: модуль Юнга EX = 2е11 Паи коэффициент Пуассона PRXY = 0,27.
Б. Аналогично раскройте DENSITY и в поле плотность DENS задайте 7800 кг/м3.
 В. Нажмите: MATERIAL => NEW
MODEL… и уже для второго материала повторяем первые две операции, присвоив:
EX = 1E+11 Па; PRXY = 0.23; DENS
= 2700 кг/м3.
В. Нажмите: MATERIAL => NEW
MODEL… и уже для второго материала повторяем первые две операции, присвоив:
EX = 1E+11 Па; PRXY = 0.23; DENS
= 2700 кг/м3.
3. Строим деталь:
А. M.M. => PREPROCESSOR => MODELING –CREATE– => –AREAS– RECTANGLE => BY DIMENSIONS…, вводим координаты углов: X1 = -0.5, X2 = 0.5, Y1 = 0, Y2 = 1, нажимаем APPLY;
Б. Вводим координаты углов: X1 = -0.3, X2 = 0.3, Y1 = 0, Y2 = 0.5;
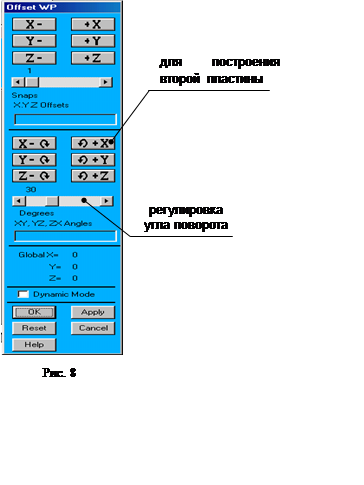
В. Для построения третьего прямоугольника повернем систему координат на угол равный 120° (рис. 9):
U.M. => WORK PLANE => OFFSET WP BY INCREMENTS…:
· угол поворота устанавливаем равным 90° и нажимаем на кнопку поворота оси Х против часовой стрелки;
· угол поворота устанавливаем равным 30° и нажимаем на кнопку поворота оси Х против часовой стрелки.
Теперь определяем координаты углов последнего прямоугольника:
 M.M. => PREPROCESSOR
=> MODELING –CREATE– => –AREAS– RECTANGLE => BY
DIMENSIONS… - X1 = -0.3, X2 = 0.3,
Y1 = 0, Y2 = 0.5.
M.M. => PREPROCESSOR
=> MODELING –CREATE– => –AREAS– RECTANGLE => BY
DIMENSIONS… - X1 = -0.3, X2 = 0.3,
Y1 = 0, Y2 = 0.5.
4. Соединяем в одно целое все полученные ранее прямоугольники, для этого:
M.M. => PREPROCESSOR =>–MODELING– OPERATE => –BOOLEANS– PARTITION => AREAS. Выделяем курсором сначала второй прямоугольник (рис. 8), затем первый и нажимаем ОК. Теперь склеиваем все пластины: M.M. => PREPROCESSOR => –MODELING– OPERATE => –BOOLEANS– GLUE => AREAS => PICK ALL. Таким образом, мы получаем единую конструкцию.
5. Назначаем каждому прямоугольнику свой материал:
M.M. => PREPROCESSOR =>–ATTRIBUTES– DEFINE => ALL AREAS… PICKED AREAS+; нажимаем на первый прямоугольник (рис. 8) и нажмите ОК, в появившемся окне выставляем: MAT = 1, REAL = 1, TYPE = 1 SHELL63, ESYS = 0 и нажимаем ОК, затем нажимаем ALL AREAS… PICKED AREAS+, потом нажимаем на второй и третий прямоугольники по очереди, нажимаем OK, затем в окне AREA ATTRIBUTES выставляем:MAT = 2, REAL = 2, TYPE = 1 SHELL63, ESYS = 0.
6. Разбиваем конструкцию на конечные элементы:
M.M. => PREPROCESSOR => –MESHING– SIZE CNTRLS => –MANUAL SIZE– –GLOBAL– SIZE…., переменной SIZE присваиваем значение 0.1, потом нажимаем ОК, затем:
M.M. => PREPROCESSOR => –MESHING– MESH => –AREAS– FREE+ => PICK ALL.
7. Проводим расчет гармонической вибрации:
А. Назначаем тип анализа – гармонический: M.M. => SOLUTION => ANALYSIS TYPE– NEW ANALISIS… => HARMONIC.
Б. Закрепляем конструкцию, как показано на рисунке 9 под цифрой 1: MM=>SOLUTION=>APPLY=>DISPLACEMENT=> LINES… и выбираем закрепляемую линию, нажимаем ОК и в появившемся окне выбираем ALL DOF, то есть по всем осям перемещения равны нулю, и нажимаем ОК.
В. Нагружаем конструкцию, как показано на рис. 9 под цифрой 2:
M.M. => SOLUTION => APPLY => PRESSURE => ON AREAS, выделяем указанную поверхность, нажимаем ОК, и в окне переменной VALUE задаем значение распределенной нагрузки равное 1000 Н/м2.
 Г. Проводим расчет:
Г. Проводим расчет:
M.M. => SOLUTION => –LOAD STEP OPTS– TIME/FREQUENC => FREQ AND SUBSTPS… и выставляем значения: HARFRQ = 4…12 – интервал частот, а NSUBST = 50 – количество шагов, STEPPED. Нажимаем ОК. Затем нажимаем MAIN MENU => SOLUTION => CURRRENT LS => OK.
6. Просматриваем результаты расчета:
А. Выбираем последовательно три узла, для которых строим графики перемещений и ускорений в зависимости от частоты нагрузки:
M.M. => TIMEHIST POSTPRO => DEFINE VARIABLES …, то есть, определяем узлы, с которых будут считываться значения перемещений. Нажимаем на кнопку ADD… и выбираем NODAL DOF RESULT, нажимаем ОК. Выбираем последовательно три узла, рис. 10, подтверждаем выбор нажатием ОК. В появившемся окне выставляем: NVAR (номер переменной) равный 2, 3 и 4 DATA ITEM равный DOF SOLUTION и TRANSLATION UY, UZ и UZ (все результаты по оси Y и Z) соответственно, нажимаем ОК потом CLOSE.
 Б. Строим графики:
Б. Строим графики:
M.M. => TIMEHIST POSTPRO => GRAPH VARIABLES… и в окне наберем: NVAR1 присвоим значение 2, NVAR2 присваиваем значение 3, NVAR3 присваиваем значение 4; и нажимаем
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.