Целевая функция математической модели градирни. Упрощения введенные при разработке математической модели

Следующим этапом исследования и решения проблемы обледенения градирни является составление математической модели объекта исследования. В ходе анализа имеющейся литературы, отчета по тепловым испытаниям градирни,  подробного изучения причины обледенения и выявления способа решения сложившейся проблемы, было принято решение о построении матмодели на основе имеющихся данных.

В ходе оценки возможных путей решения сложившейся проблемы, в качестве эксперимента был рассмотрен вариант использования верхних воздуходувных окон в градирне, в которые должен подаваться холодный воздух окружающей среды по специальным воздуховодам. Принцип действия этих окон в следующем: с внешней стороны градирни устанавливаются воздуховоды, по которым холодный и сухой воздух окружающей среды подается через окна внутрь градирни под определенным углом и отделяет холодные стенки от влажного воздуха, тем самым исключается обледенение. Это решение основано на принципе устранения взаимодействия двух веществ, «вредно» влияющих друг на друга. Конструктивно, данный способ решения проблемы обледенения представлен на рисунке 5.1.

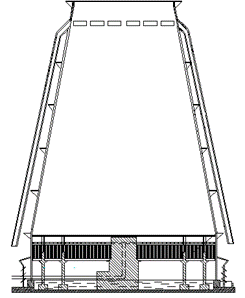
Рисунок 5.1 – Башенная градирня с внешними воздуховодами

5.1 Целевая функция математической модели градирни

Критерий эффективности научно-технического мероприятия, проекта или решения должен отражать соотношение между ожидаемым полезным эффектом и затратами, необходимыми для получения этого полезного эффекта. При этом, однако, не следует забывать, что показатели полезного эффекта и затрат, определяющие целевую функцию, являются приближенными. Поэтому в основном важно, чтобы выбранный критерий был по возможности простым, критичным по отношению к оптимизируемым параметрам и достаточно наглядным, т.е. имел физический смысл.

При технико-экономической постановке оптимизационных задач используются целевые функции, различающиеся физическим смыслом входящих в них показателей полезного эффекта и затрат. Так, в стационарной и судовой энергетике оптимальный вариант установки часто определяется в результате минимизации приведенных затрат (годовых или за весь срок службы) на установку при постоянном значении ее мощности.

Такая форма представления целевой функции имеет свои трудности. Во-первых, исследователь или проектировщик должен знать заранее величину полезного эффекта, что не всегда возможно. Во-вторых, при этом возникает дополнительная проблема приведения сравниваемых вариантов к одинаковому полезному эффекту. В частности для ТЭС в конечном счете все затраты сводятся к стоимости 1кВт/ч.

Чтобы избежать этих трудностей, критерий эффективности представляют в виде отношения затрат к соответствующему полезному эффекту или, наоборот, полезного эффекта к затратам [11].

Целью создания математической модели противоточной градирни является изучение принципа работы градирни как элемента ТЭС. Проведение исследований по  повышению надежности работы градирни в зимний период