Основы эконометрики. Теоретические материалы для студентов ОФиП. Корреляционный анализ

Вероятностная зависимость между признаками, в общем случае, не имеет строго функционального характера. В отличие от функциональной такой род зависимости предполагает дополнительное влияние некоторых случайных факторов, воздействие которых приводит к различным случайным отклонениям.

Так, например, известно, что при увеличении товарооборота издержки обращения также увеличиваются. Однако на практике может возникнуть ситуация, когда у предприятия с меньшим товарооборотом наблюдаются большие издержки. Но если рассматривать достаточно большую группу предприятий, то в среднем эта зависимость будет иметь место. 

Перед проведением корреляционного анализа полезно выяснить, в каких шкалах измеряются интересующие нас показатели, поскольку от этого зависят способы проведения корреляционного анализа. В этой связи различают корреляционный анализ в сильных и слабых шкалах. 

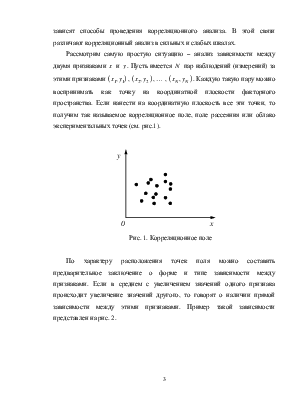
Рассмотрим самую простую ситуацию – анализ зависимости между двумя признаками x и y . Пусть имеется N пар наблюдений (измерений) за этими признаками (x y_{1 1}, ), (x y_{2 2}, ), … , (x y_N , _N ). Каждую такую пару можно воспринимать как точку на координатной плоскости факторного пространства. Если нанести на координатную плоскость все эти точки, то получим так называемое корреляционное поле, поле рассеяния или облако

экспериментальных точек (см. рис.1). 

Рис. 1. Корреляционное поле

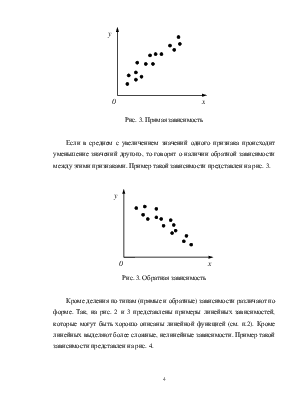
По характеру расположения точек поля можно составить предварительное заключение о форме и типе зависимости между признаками. Если в среднем с увеличением значений одного признака происходит увеличение значений другого, то говорят о наличии прямой зависимости между этими признаками. Пример такой зависимости представлен на рис. 2. 

Рис. 3. Прямая зависимость

Если в среднем с увеличением значений одного признака происходит уменьшение значений другого, то говорят о наличии обратной зависимости между этими признаками. Пример такой зависимости представлен на рис. 3. 

Рис. 3. Обратная зависимость

Кроме деления по типам (прямые и обратные) зависимости различают по форме. Так, на рис. 2 и 3 представлены примеры линейных зависимостей, которые могут быть хорошо описаны линейной функцией (см. п.2). Кроме линейных выделяют более сложные, нелинейные зависимости. Пример такой зависимости представлен на рис. 4.

Рис. 4. Нелинейная зависимость

Однако выводы, основанные только на визуальном восприятии формы корреляционного поля, могут быть ошибочными. Большую роль здесь может играть масштаб осей координат и субъективность восприятия.

2.1. Коэффициент корреляции и его свойства

Объективные выводы должны опираться на строгие математические расчеты. Одним из самых распространенных способов измерения тесноты связи между двумя признаками является парный коэффициент корреляции, который может быть вычислен по следующей формуле:

xy − x y⋅

                                                                    r_xy =,                                         (1)

                                                                                                     S Sx y

                                N                                                  NN

где x = ¹ ∑x_i ; y = ¹ ∑ y_i ; xy = 1 ∑x y_{i i} ; S_x – среднеквадратичное

                        N i=1                        N i=1                          N i=1

отклонение для признака x; S_y – среднеквадратичное отклонение для признака y . 

В общем случае, среднеквадратичное отклонение определяется как квадратный корень из дисперсии признака S_x = σ_x² . Но, как правило, истинное значение дисперсии σ_x² не известно, а по имеющимся данным определяется так называемая выборочная дисперсия признака. Вычисление выборочной дисперсии можно проводить двумя способами:

1 N

                                                         s x     x ,                                         (2) 

N i=1

N

                                                     S 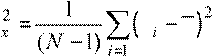x     x .                                     (3) 

Выборочная дисперсия (3) является несмещенной оценкой величины σ_x², в то время как выборочная дисперсия (2) смещена относительно истинного

2

значения σ_x² на величину ^σx _N [15].

Очевидно, что величины (2) и (3) связаны между собой соотношением

                                                            Sx2 = N sx2.                               (4)

(N −1)

Из этого соотношения следует, что оценка (2) является более эффективной, т.е. обладает меньшей дисперсией. Кроме того, при достаточно большом количестве наблюдений