Примеры решения задач по дисциплине "Высшая математика", страница 2

ТЕОРЕМА

Вероятность подменил хопи бы одного из Двух сокмеспшьјх событий равна сумме вероятностей этих событий без вероятности Их сокМестлого появления:

Р(А+В) = ЛА) + ЦВ) -

Замоим, что эта же формула верна и для несовместных событий, поскольку вероятность их совместного появления равна О и в этом случае получаем формулу, уже известную нам как свойство З вероятности.

         ПРИМЕР        

Найти вероятность того, что при броске игральной кости или выпало чет-

ное число очков, или число выпавших очков больше 4.

Решение

Обозначим первос событие через А (выпало четное число очков), втрое — через В. Нас интересуег значение Р(А+В). Заметим, что ЦВ) = 2/6 =  1,¹3, а Р(ЛВ) = = 1/2-1/3 —1/6. Таким образом, по теореме о вероятности суммы событий, интересующая нас вероятность равна

12

) (сйспвтејп,но. если мы подсчитаем количество благоприятных исходов неио('.рсдсгвенио. то убедимся. что пас утраивают 4 исхода из 6 возможных: выпадспис 2, 4, 5 или 6 ОЧКОВ.

Формула полмой вероятности и формула Бейеса.

            Рассмогрим набор собьпий                       Говорим, что              набор образусг

полную группу событий, если т.е. при испытании с достовернослыо произойдёт Хотя бы одно

11апример, рассмотрим бросок игральной кости и следующие события:

А = {выпало «мое число очков},

 В {выпало неч&жое число очков! , {выпало 5 очков),

1) — (выпало меньше 5 очков}.

 Тогда события А и В, Л и С и 1), А и В и С, А ив и ДА и В и С и D образую•г полные !руппы собьпий, а остальные комбинации событий полную группу не образуют.

Пусть событие А может наступить при усјювии появления одного из попарно несовместных событий В„..., Вт которые образуют полную 1руппу собызий. Пусть известны вероязтюсги всех лих событий и устовные вероятности Рв (А). Как найп•и вероятность события А? (_Угвег на эгот вопрос дает следующая

ТЕОРЕМА (формула полной вероятности)

Вероятность события А, которое может наступить лишь при условии поямения одного цз попарно несовместных событий Вь..., Вт образующих полную группу, равна сумме произвеДений вероятностей кажДого из этих событий на соответспщующую условную верояпшость события А:

ПРИМЕР

Студент приходит на экзамен, притхловив сугветы на 45 вопросов из 60. Вероятность ответить правильно на знакомый вопрос равна 09, а на незнакомый — 0.05. Какова вероятность для студента правильно отвиить на первый вопрос?

Решение

Введём обозначения. Пусть событие А означавг, что первый вопрос сту-

денту знаком, а В — что он ответил на первый вопрос правильно. Тогда событие Л означает, что первый вопрос ему незнаком. Заметим, что события А и образунуг полную группу событий (как любые два противоположных событуш). По условию, РА(В) = 09, а По классическому определению

тщательно перемешиват• и вытаскиваюг шар из второго ящика. Какова верт вероятнослм, Р(Л)Нас инлересуег значениеялмосп, лого, что втащенный шар — белый? Чёрный?

Решение

Р(В). По формуле полной верошмости Пусть собылме Л означает. что из первојо ящика вылощили белый шар, а событие В соответствует вытаскиванию белого шара из второго ящика в ходе испытжния. Нас интересуют значения вероятносзей Р(В) и Р(В ). Заметим, что события А и А образуют полную группу событий. По классическому определеЗаметим, что такая достаточно большая вероятность дослигаш•ся не за счёг не-2 5 значительной возможности правильно ответить на незнакомый вопрос, а за ник) вероятности, 7 7 Найдем условные вероятности РА (В) и счет достатоЧН0 хорошей подготовки студента к экзамену — как никак, 45 во-РЫВ):

просов из 60 он выучил. Делайте выводы!

                Предположим, что в условиях предыдущей теоремы событие А произошло.                                

1 [оскольку мы не знаем, какое из событий В„..., произошло. будем эти собы-Ио формуле полной вероятности,

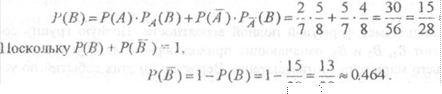зия называть гипотезами. Можно ли утверждать, что гипотеза В, справедлива с„0.536.

искоторой веротгностью, т.е. возможно ли оценить условную вероятность  Положительный ОЛВСУТ на этог вопрос даег следующая формула Бейеса

(или Байеса):

ПРИМЕР 2

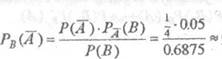
Некоторая продукция изготовлена на зрёх станках, причём первый станок произвел 50⁰/0 продукции, второй — 30⁰/0 и третий — остальные 20⁰/6 продукции. ПРИМЕР Известно, что вероятность брака для первого станка составляет 0.05, для второПусть в условиях предыдущего примера студент отвемл на вопрос пра- го — 0.1 и для третьего ().15. Наугад выбранный экземпляр продукции оказалвильно. Какова вероятность того, что первый вопрос был ему не знаком? ся бракованным. Какова вероятность того, что он был произведён на первом Решениестанке? На втором станке? На третьем станке?

В этом примере гипотезами служат события А и , определённые выше вРешение решении, а событие В считается уже произошедшим, т.е. достоверным. ИскомаяРассмотрим гиш_иезы Щ, 132 и Вз, состоящие в том, что рассматриваемый

вероятность равнаэкземпляр выпущен на первом, втором и третьем станке соответственно. Собы-