Электромагнитные колебания.
Колебания- это периодический процесс, при котором система много раз проходит через положение равновесия.
Отклонение системы
от положения равновесия называется смещение. Максимальное смещение
называется амплитуда. Время одного полного колебания называется период
[с]. Число колебаний за секунду называется частота [с-1=
Герц= Гц]. 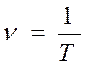 , ν –ч астота, Т –
период.
, ν –ч астота, Т –
период.
Фаза колебания φ – отклонение от равновесия, выраженное в угловой мере или долях периода (один период соответствует углу 2π). Фазу в начальный момент времени (t = 0) называют начальной фазой φ0.
Колебания делятся на свободные и вынужденные. Свободные колебания происходят под действием внутренних сил (причин) системы с частотой, которая зависит от параметров (характеристик) системы. Вынужденные колебания происходят под действием внешней периодической силы. Частота вынужденных колебаний равна частоте внешней вынуждающей силы.
Электромагнитные колебания
(ЭМК) – это колебания заряда,
напряжения, энергии в колебательном контуре, состоящем из конденсатора С,
индуктивности L и резистора (сопротивления) R. Конденсатор,
заряженный до заряда q0 и
напряжения U0 ,
разряжается через L, в которой возникает ЭДС самоиндукции 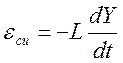 , которая задерживает изменение тока, пэтому
конденсатор перезаряжается и процесс (ток) идет в обратную сторону.
, которая задерживает изменение тока, пэтому
конденсатор перезаряжается и процесс (ток) идет в обратную сторону.
Диф. уравнение свободных колебаний.
По закону Кирхгофа ЭДС,
действующая в эл. цепи, равна сумме напряжений в этой цепи. В колебательном
контуре ![]()
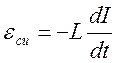 UR =I· R UC =
UR =I· R UC =![]() ,
, 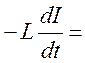 I· R +
I· R + ![]() = 0,
но I=
= 0,
но I=![]()
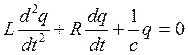 ,
разделим выражение на L,
,
разделим выражение на L, 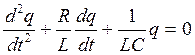 (1)
Это дифференциальное уравнение затухающих свободных колебаний II порядка.
(1)
Это дифференциальное уравнение затухающих свободных колебаний II порядка.
Обозначим
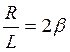 ,
, 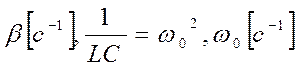
β –называется коэффициент затухания. ω0 – собственная циклическая (круговая) частота свободных колебаний.
Если контур имеет R (реальный контур), то на нем происходит переход энергии колебаний в тепло, т. е. потеря энергии. Такие колебания называются свободными затухающими колебаниями.
Если в контуре R=0, то потери энергии колебаний нет. Энергия постоянна. Такие колебания называются свободными незатухающими колебаниями. Для них диф. уравнение легко получить, положив R=0.
-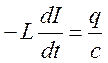
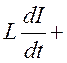
![]() =0 I =
=0 I =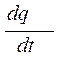
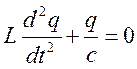
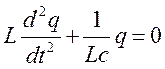
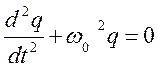 (2)
(2)
Решение этого уравнения q= q0 sin (ω0 t ![]() φ0) или q0 cos (ω0 t
φ0) или q0 cos (ω0 t ![]() φ0)
φ0)
q= qmaх е –βt
sin (ωзt ![]() φ0) или q= qmах
е –βt
cos (ωзt
φ0) или q= qmах
е –βt
cos (ωзt ![]() φ0)
φ0)
ωз = ![]()
q mах - начальная, максимальная амплитуда колебаний.
Свободные незатухающие электромагнитные колебания.
q – заряд конденсатора в момент t.
q 0 – амплитуда заряда.
ω0 –
собственная круговая частота ![]() (с-1)
(с-1)
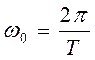 =2πν
=2πν
φ0 –начальная фаза колебаний.
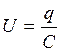 ,
поэтому U= U0 sin (ω0 t
,
поэтому U= U0 sin (ω0 t 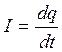 I = q' = (q0 sin (ω0 t
+φ0)) !
I = q' = (q0 sin (ω0 t
+φ0)) ! q 0 ω0 = I0 – амплитуда тока в контуре.
Энергия колебаний равна сумме энергии электрического поля, заключенного в конденсаторе, и энергии магнитного поля,заключенного в катушке индуктивности
w = wэп + wмп.
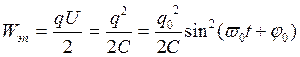
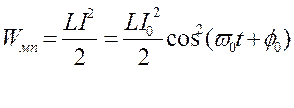
Между Wэп и W мп имеется сдвиг фаз ![]() , т.е. если Wэп = мах, то Wмп = 0 и наоборот. Поэтому полная энергия колебаний
, т.е. если Wэп = мах, то Wмп = 0 и наоборот. Поэтому полная энергия колебаний
W =(Wэп )мах
= (Wмп )мах
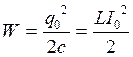
Для незтухающих колебаний W= const, следовательно амплитуда таких колебаний равна const.
Формула таких колебаний
q = q max e –βt sin (ω з t + φ 0)
Имеет две функции
a) q max e –βt – это функция изменения амплитуды колебаний со временем б). sin (ω з t + φ 0) -1 это функция изменения смещения со временем.
q 0 = q max e –βt
Чтобы определить смысл
коэффициента затухания β , приравняем β =![]() , тогда q 0 = q m e –1 =
, тогда q 0 = q m e –1 = ![]() ,
т.е.β - величина, обратная времени, за которое амплитуда уменьшается в е раз
(е = 2,73…) . Следовательно коэффициент затухания определяет скорость
затухания: чем больше, тем быстрее уменьшается амплитуда.
,
т.е.β - величина, обратная времени, за которое амплитуда уменьшается в е раз
(е = 2,73…) . Следовательно коэффициент затухания определяет скорость
затухания: чем больше, тем быстрее уменьшается амплитуда.
Скорость затухания определяет также декремент. Это отношение двух амплитуд, разделенных периодом
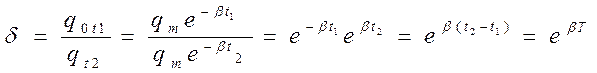
t2 = t1 +T
Часто используют логарифмический декремент
Λ= ln![]() =lne
βT = βT
=lne
βT = βT
Полная энергия колебаний W
= 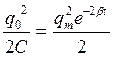 ,т. е. она уменьшается со временем.
,т. е. она уменьшается со временем.
Вынужденные колебания.
Уравнение вынужденных колебаний
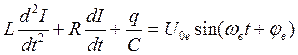 , где
, где 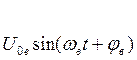 Внешняя периодическая сила
(напряжение) действующая с вынуждающей
круговой частотой ωв. Вынужденные колебания происходят по формуле q = q0 sin(ωв t+ Q), где ωв -частота
вынужденных колебаний равна частоте вынуждающей силы. Q- разность фаз
между вынужденными колебаниями и вынуждающей силой.
Внешняя периодическая сила
(напряжение) действующая с вынуждающей
круговой частотой ωв. Вынужденные колебания происходят по формуле q = q0 sin(ωв t+ Q), где ωв -частота
вынужденных колебаний равна частоте вынуждающей силы. Q- разность фаз
между вынужденными колебаниями и вынуждающей силой.
q0 -
Амплитуда вынужденных колебаний, которая зависит от соотношения частоты вынужденных колебаний ωв и собственной частоты свободных колебаний ωз колебаний
Когда частота вынужденных колебаний и собственная частота сильно различаются, амплитуда мала. При сближении частот амплитуда значительно возрастает, достигая максимума. При некоторой частоте, которая называется резонансной частотой.
ωрез = ![]() ,если β <<ω0, то ωрез ≈ ω0.
,если β <<ω0, то ωрез ≈ ω0.
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынужденны колебаний к резонансной частоте называется резонансом.
1. Сложение колебаний одинаковых частот, направленных по одной прямой. X1 = X01 sin(ωt+φ01) X2 = X02 sin(ωt+φ02)
X = X01 sin(ωt+φ01) + X02 sin(ωt+φ02) = X0p sin(ωt+φ0p)
X0p - амплитуда результирующего колебания
Φ0p - начальная фаза результирующего колебания
Можно показать, что X0p=![]()
(под знаком корня квадратного
выражение полностью) а) Если ![]() где к = 0,1,2,3…., то cos (φ01
– φ02) =1 и
где к = 0,1,2,3…., то cos (φ01
– φ02) =1 и
Х0р= Х01+Х02.
б) Если (φ01 – φ02) = (2к+1)π , то cos (φ01 – φ02) = -1 и
Х0р= Х01-Х02.
2 tg φ0р =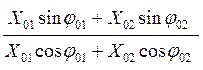
2. Сложение колебаний, направленных по одной прямой с разными частотами.
X1 =X01sin (ω1t +φ01), X2 =X02sin (ω2t +φ02)
X р = X01sin (ω1t +φ01) +X02 sin (ω2t +φ02), для простоты Х01 = Х02 = Х0
φ01 = φ02 = 0, ω1 ≈ ω2
Хр = Х0 [sinω1t + sinω2t] [sin![]() sinβ = 2sin
sinβ = 2sin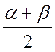 cos
cos 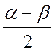 ]
]
X p= 2X0sin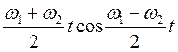
Результирующие колебания
происходят с частотой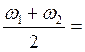 ω средняя,
а амплитуда этих колебаний меняется с малой частотой
ω средняя,
а амплитуда этих колебаний меняется с малой частотой 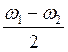 . Такие колебания называются биения
(модулированные колебания)
. Такие колебания называются биения
(модулированные колебания)
3. Сложения перпендикулярных колебаний.
Х = Х0 sin (ω1t + φ01) Y = Y0 sin(ω2t + φ02)
Х + Y= Х01 sin (ωt + φ01) +Y0 sin(ωt + φ02)
Точка, которая должна одновременно колебаться по оси Х и оси Y, будет двигаться по траектории эллипс, формула которого
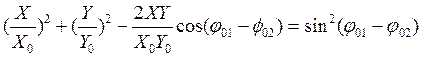
Разложение сложных колебаний.
Простое или гармоническое колебание описывается функцией sin или cos. Сложные колебания, не гармонические, не всегда можно описать одной функцией,но если сложное колебание периодическое, то его можно представить как сумму простых гармонических колебаний.
Теорема Фурье: любое сложное периодическое колебание можно разложить на сумму простых гармонических колебаний, частоты которых кратны частоте сложного колебания:
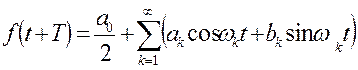 , где к= 0, 1, 2, 3 …. Или
, где к= 0, 1, 2, 3 …. Или
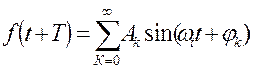 = A1 sin(ω1t +φ1)
+ A2 sin(ω2t +φ2) + A3
sin(ω3t +φ3)+….
= A1 sin(ω1t +φ1)
+ A2 sin(ω2t +φ2) + A3
sin(ω3t +φ3)+….
Каждый член этой суммы называется к-гармоникой. Частота к-гармоники в к-раз больше частоты сложного колебания.
ωк = к ω = кω1
Совокупность всех гармоник, на которые разлагаются данное сложное колебание, называется гармоническим спектром данного колебания. Очевидно этот спектр линейчатый или дискретный.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.