



2 Физико-математическая моделирование акустооптического эффекта в магнитоэлектриках
Рассмотрим определённо поляризованный в магнитоэлектрике свет, который разделяется на обыкновенно и необыкновенно поляризованные лучи. Эти лучи направляются в акустическую ячейку под углами, удовлетворяющими условиям Брэгга для обыкновенно (о) и необыкновенно (е) поляризованного света [5].
Брэгговская дифракция может рассматриваться как процесс рассеяния фотонов на фононах, происходящий с выполнением законов сохранения энергии и импульса. Векторные соотношения записываются в виде:
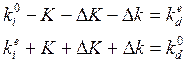 ,
(2.1)
,
(2.1)
где ki, и kd — волновые векторы падающего и дифрагированного света для обыкновенно и необыкновенно поляризованных лучей, K — волновые векторы звука, ΔК и Δк — приращения акустического вектора и векторы расстройки [1].
В
соответствии с формулой вектор kd0 образуется
как сумма, а вектор kde — как разность волновых векторов падающей
световой и акустической волн. Векторная
диаграмма, иллюстрирующая соотношение, представлена
на рис. 3. На этом рисунке показана оптическая
ось кристалла [001] и углы Брегга ![]() и
и ![]() .
Акустичские волны распространяются в кристалле под углом
.
Акустичские волны распространяются в кристалле под углом ![]() к оси
[110] в плоскости акустооптического взаимодействия,
как показано на рисунке 4.
к оси
[110] в плоскости акустооптического взаимодействия,
как показано на рисунке 4.
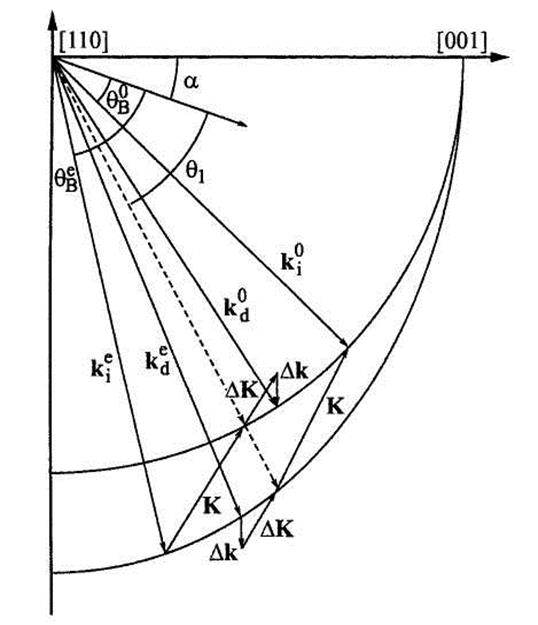
Рисунок 3 Векторная диаграмма акустооптического взаимодействия для обыкновенно (о) и необыкновенно (е) поляризованного света, где ki, и kd — волновые векторы падающего и дифрагированного света, K — волновые векторы звука, ΔК и Δк — приращения акустического вектора и векторы расстройки.
Известны соотношения
для длин волновых векторов взаимодействующих пучков ![]() ,
, ![]() ,
,
![]() , где
V — фазовая скорость звука,
, где
V — фазовая скорость звука, ![]() и
и
![]() — частота акустической волны и ее вариации при нарушении
условий синхронизма.
— частота акустической волны и ее вариации при нарушении
условий синхронизма.
В магнитоэлектриках измерение угла поворота плоскости поляризации ![]() , выражается формулой [4]:
, выражается формулой [4]:
![]() ,
(2.2)
,
(2.2)
где ![]() - напряженность магнитного поля,
- напряженность магнитного поля, ![]() - длина намагниченной части образца и
- длина намагниченной части образца и
![]() - постоянная Верде, которая содержит в
себе информацию о свойствах, присущих исследуемому образцу, и может быть
выражена через микроскопические параметры среды. При λ = 630нм и длине образца
- постоянная Верде, которая содержит в
себе информацию о свойствах, присущих исследуемому образцу, и может быть
выражена через микроскопические параметры среды. При λ = 630нм и длине образца ![]() постоянная
Верде
постоянная
Верде ![]() °·А-1 [6].
°·А-1 [6].
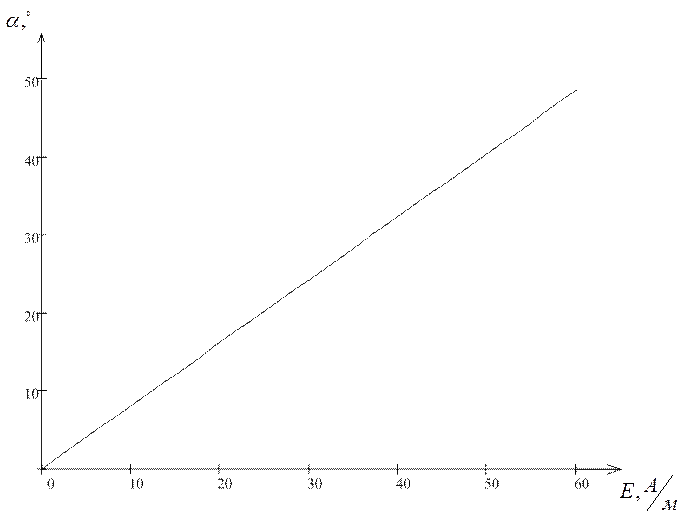
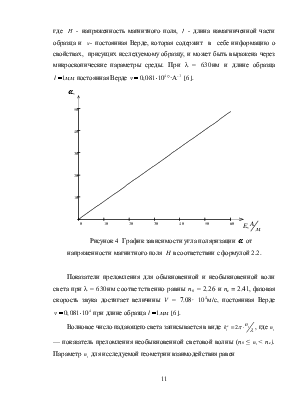
Рисунок 4
График зависимости угла поляризации ![]() от
напряженности магнитного поля
от
напряженности магнитного поля ![]() в соответствии с формулой 2.2.
в соответствии с формулой 2.2.
Показатели
преломления для обыкновенной и
необыкновенной волн света при λ = 630нм
соответственно равны п0 = 2.26 и пе = 2.41, фазовая скорость звука достигает величины V =
7.08∙ 104м/с, постоянная Верде ![]() при
длине образца
при
длине образца ![]() [6].
[6].
Волновое число падающего света записывается в виде ![]() , где
, где ![]() —
показатель преломления необыкновенной
световой волны (п0 ≤
—
показатель преломления необыкновенной
световой волны (п0 ≤ ![]() <
пе). Параметр
<
пе). Параметр ![]() для исследуемой геометрии
взаимодействия равен
для исследуемой геометрии
взаимодействия равен
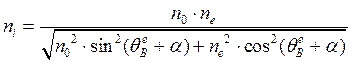 . (2.3)
. (2.3)
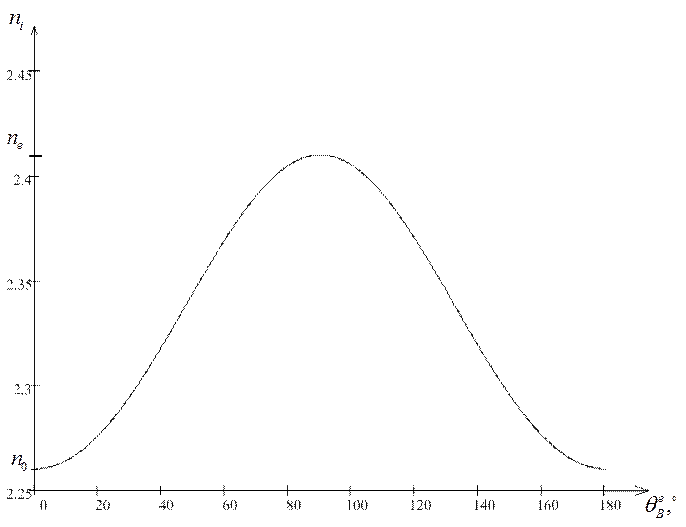
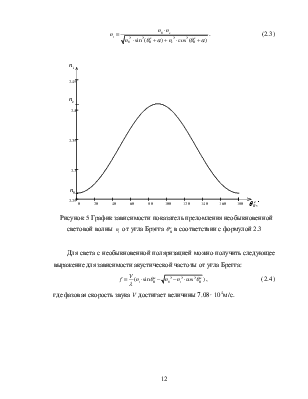
Рисунок 5 График зависимости показатель преломления необыкновенной световой волны ![]() от угла Брэгга
от угла Брэгга ![]() в соответствии с формулой 2.3
в соответствии с формулой 2.3
Для света с необыкновенной поляризацией можно получить следующее выражение для зависимости акустической частоты от угла Брегга:
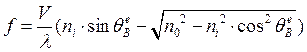 , (2.4)
, (2.4)
где фазовая скорость звукаV достигает величины 7.08∙ 104м/с.
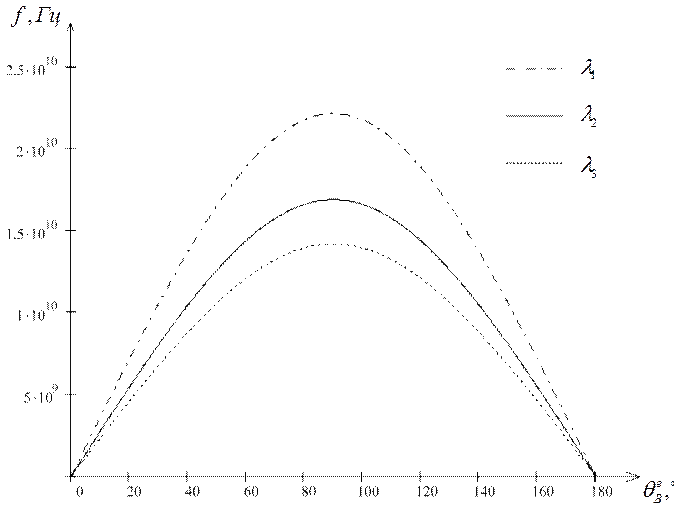
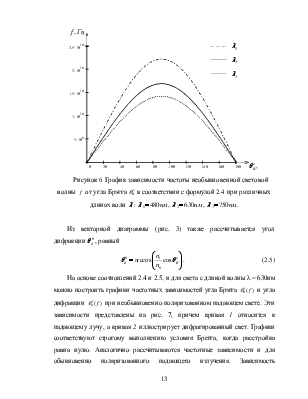
Рисунок 6 График зависимости частоты необыкновенной световой волны ![]() от угла Брэгга
от угла Брэгга ![]() в соответствии с формулой 2.4 при различных длинах волн
в соответствии с формулой 2.4 при различных длинах волн ![]() :
:
![]() ,
, ![]() ,
, ![]() .
.
Из
векторной диаграммы (рис. 3) также рассчитывается угол дифракции ![]() ,
равный
,
равный
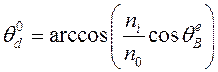 . (2.5)
. (2.5)
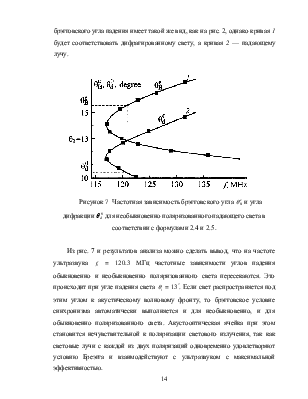
На
основе соотношений 2.4 и 2.5, и для света с длиной волны λ = 630нм можно
построить графики частотных зависимостей
угла Брэгга ![]() и угла дифракции
и угла дифракции ![]() при
необыкновенно поляризованном падающем свете
при
необыкновенно поляризованном падающем свете
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.