Задание:
po = -70, p1 = 4, p2 = 6, p3 = -1, p4 = 0, p5 = -2
По заданным нулю и пяти полюсам передаточной функции разомкнутой системы записать и определить:
1. передаточную функцию разомкнутой системы
2. передаточную функцию замкнутой системы
3. дифференциальное уравнение системы
4. структурную схему замкнутой системы
5. АЧХ разомкнутой системы
6. ФЧХ разомкнутой системы
7. АФХ разомкнутой системы
8. весовую и передаточную функцию разомкнутой системы
9. ЛАЧХ (асимптотическую) разомкнутой системы
Проанализировать устойчивость замкнутой системы методами Рауса-Гурвица, Михайлова и Найквиста.
Проанализировать устойчивость замкнутой системы по асимптотической ЛАЧХ и ЛФЧХ.
Если система устойчива, определить запасы устойчивости по частоте и фазе.
Если система не устойчива, дать рекомендации по обеспечению устойчивости и построить ЛАЧХ скорректированной системы.
Решение:
Передаточная функция разомкнутой системы
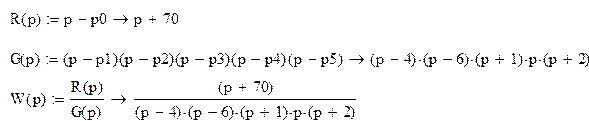
Передаточная функция замкнутой системы
![]()
Дифференциальное уравнение системы
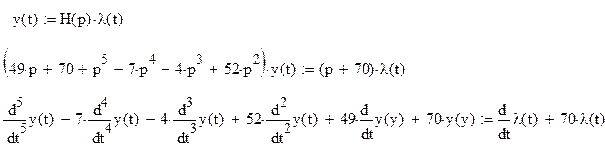
Структурная схема замкнутой системы
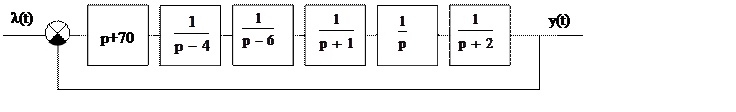
Анализ исследуемой цепи
АЧХ разомкнутой системы
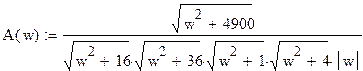
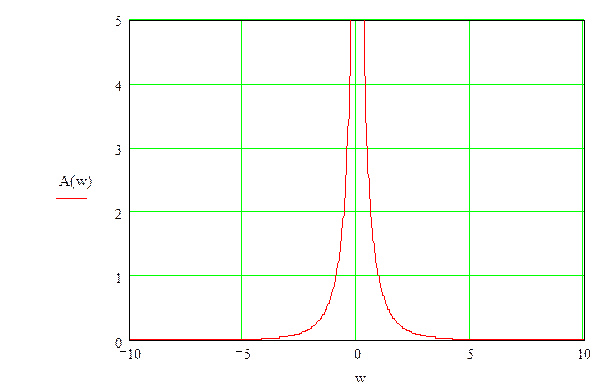
ФЧХ разомкнутой системы
![]()
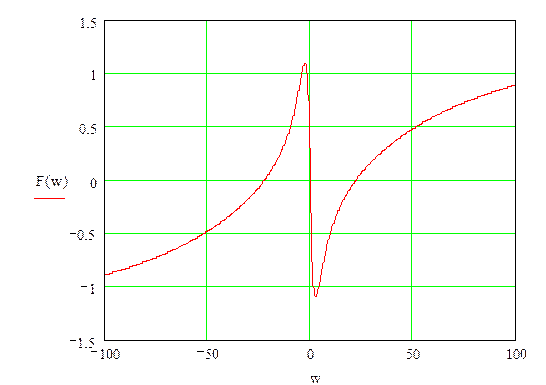
АФХ разомкнутой системы
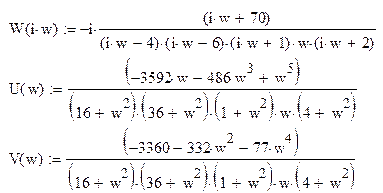
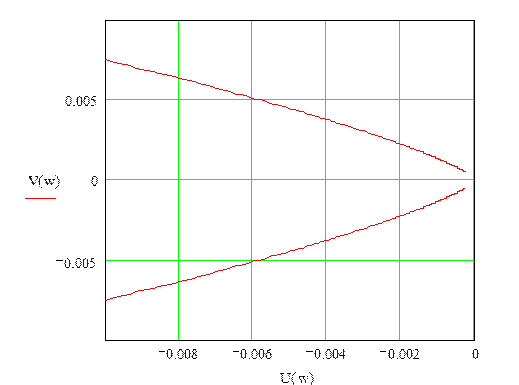
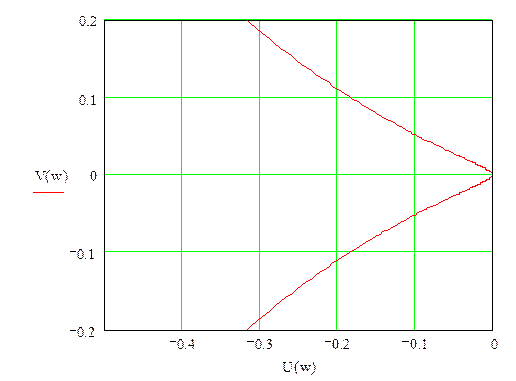
Весовая и передаточная функции разомкнутой системы
![]()
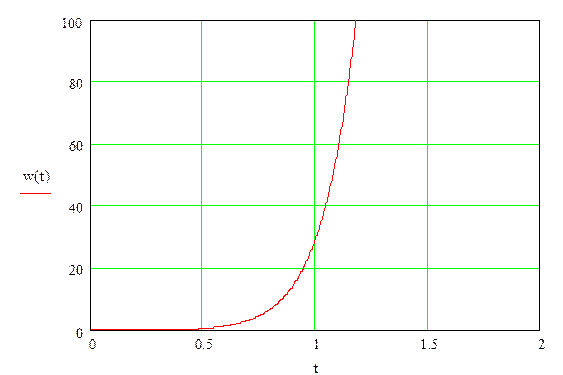
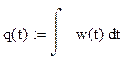
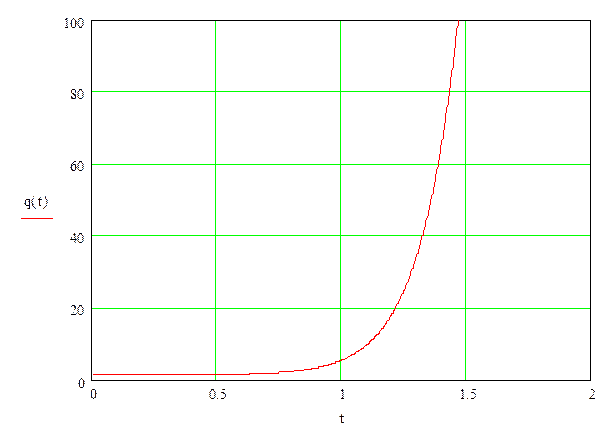
ЛАЧХ (асимптотическую) разомкнутой системы
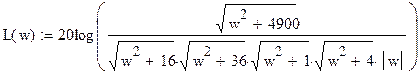
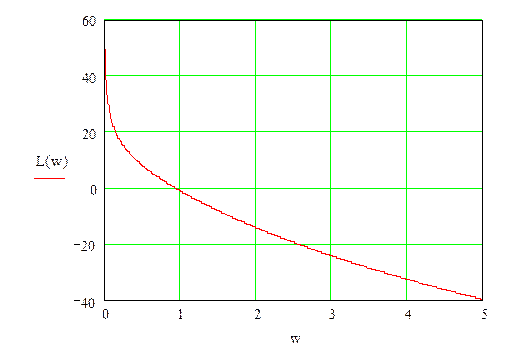
Анализ устойчивости системы:
Метод Рауса-Гурвица
Данный критерий является алгебраическим и базируется на анализе определителя Рауса, который составляется на основе характеристического уравнения.
![]()
Так как в характеристическом уравнении есть отрицательные коэффициенты, то система неустойчива.
Критерий Михайлова
![]()
Годограф:
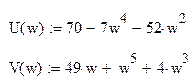
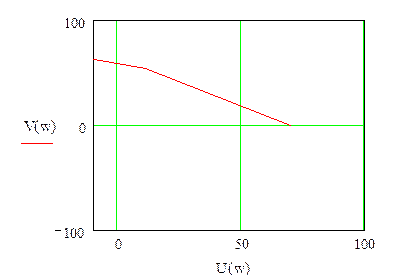
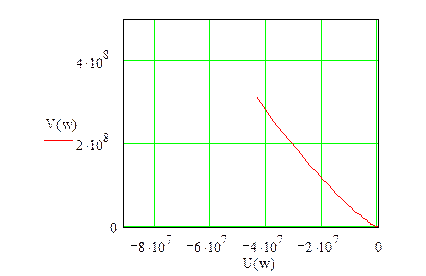
Так как годограф из второй четверти не возвращается в первую через третью и четвертую, то делаем вывод, что система неустойчива.
Критерий Найквиста
Необходимо и достаточно, чтобы функция в плоскости комплексной переменной была замкнута и не охватывала точку (-1; j0).
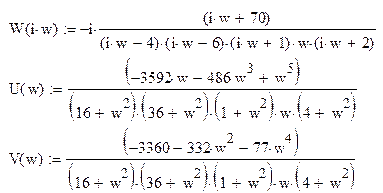
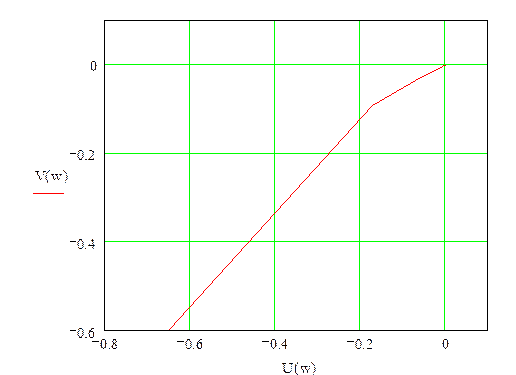
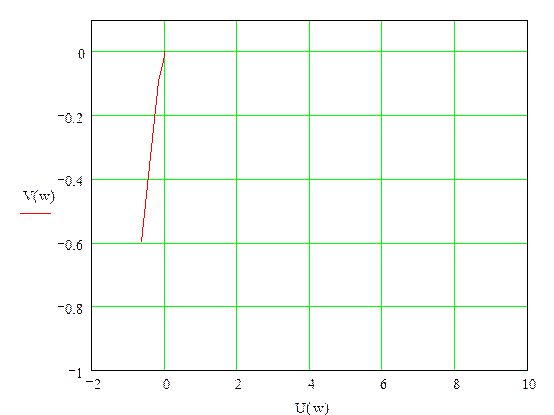
Дополнив годограф дугой большого радиуса мы видим, что при увеличении частоты годограф вращается почасовой стрелки, тем самым он охватывает точку
(-1; j0). Поэтому система неустойчива.
Анализ устойчивости системы по асимптотической ЛАЧХ
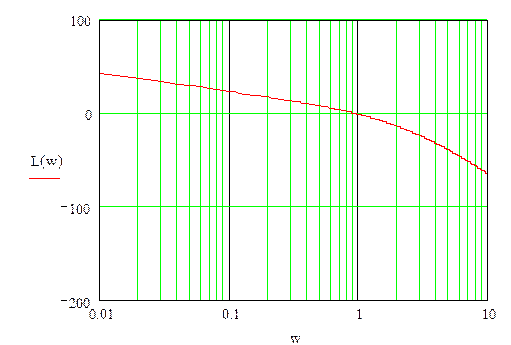
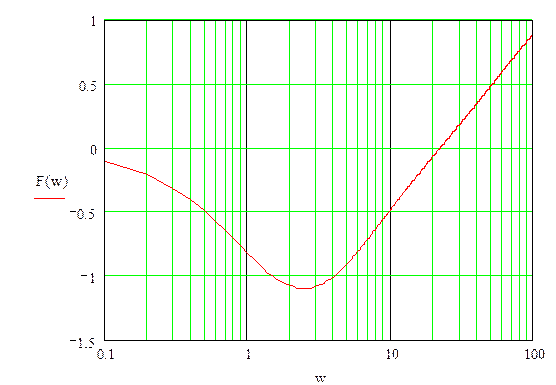
Так как ЛФЧХ не пересекает -π, то система неустойчива
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.