Построение математической модели процесса изменения сопротивления резисторов от температуры

Федеральное агентство по образованию

Государственное образовательное учреждение

Высшего профессионального образования

«Владимирский Государственный Университет»

Кафедра «Конструирования и технологии радиоэлектронных средств»

Лабораторная работа №2

Проведение и обработка результатов пассивного эксперимента

                                                                               Выполнил:

                                                                                             студент гр. РЭ-108

                                                                                          

                                                                               Проверил:

                                                                                     

Владимир 2010

Цель работы. Построение математической модели процесса изменения сопротивления резисторов от температуры.

Теоретические сведения.

Целью пассивного эксперимента часто бывает построение математической модели зависимости у=f(x₁,x₂,...,x_n). В основе построения математических моделей обычно лежит регрессионный анализ. При построении математических моделей на основе пассивного эксперимента нужно решить следующие задачи:

проверить постулаты регрессионного анализа;

построить математическую модель;

проверить адекватность модели;

проверить значимость коэффициентов модели (коэффициентов регрессии).

Регрессионный анализ имеет три постулата:

1)  выходной параметр имеет нормальный закон распределения;

2)  факторы (первичные параметры) есть неслучайные величины (на практике <<);

3) точность определения выходного параметра у не зависит от величины у (дисперсии у должны быть однородны в различных точках факторного пространства). Однородность дисперсии проверяется с помощью критериев Фишера, Бартлета, Кохрена.

Математически модели строятся обычно в виде полиномов:

- линейных:

у=b₀ + b₁ x₁ - однофакторное пространство;

у = b₀ + b₁x₁ + b₂x₂ - двухфакторное пространство;

- нелинейных.

Определение коэффициентов моделей обычно проводится с использованием метода наименьших квадратов (МНК). Суть его в следующем.

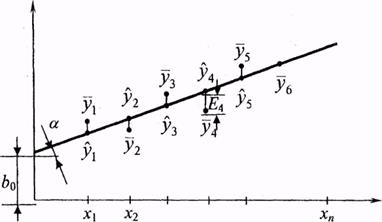
Рис. 1. Зависимость у=b₀ + b₁ x₁

Пусть (i=1,2,...n) - средние значения  у_i  (рис.  1), полученные призначениях параметров (факторов) x_i. Будем аппроксимировать полученные экспериментальные значения линейных полиномов вида у=b₀ + b₁ x₁, где коэффициент равен ординате, a b₁ = tg α .

Разность между  и у_i на модели и средними экспериментальными значениями  обозначим E_i

При МНК линия, определяющая зависимость y=f(x) должна проводиться таким образом, чтобы сумма квадратов отклонений между средними значениями и точками модели была минимальной:

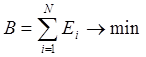
Условием нахождения минимума является выполнение условий:

,

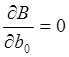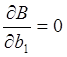
Можно записать

, ;

, .

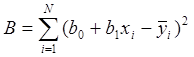
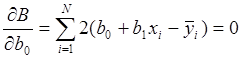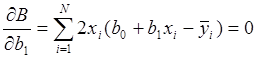Получаем систему уравнений, называемую системой нормальных уравнений.

Решая её, найдём

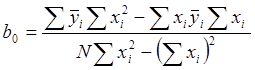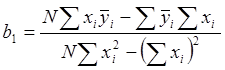,                                  (1), (2)

Коэффициенты уравнения регрессии часто называют коэффициентами регрессии.

Проверка адекватности модели производится при помощи критерия Фишера:

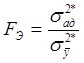,                                                                   (3)

где   - дисперсия адекватности;

 - дисперсия воспроизводимости.

Если F_э < F_т(f₁,f₂) при заданном p, где F_т(f₁,f₂) - табличное значение критерия Фишера, то считается, что модель адекватна, в противном случае -неадекватна. Число степеней свободы f₁ и f₂:

f₁=N-(k+1),   f₂=N, где k+1 равно числу коэффициентов регрессии, k равно числу факторов.

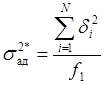,                                                               (4)

где .

Дисперсия воспроизводимости - это дисперсия среднего значения выходного параметра . Дисперсия в i-м сечении:

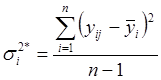
где п - число параллельных опытов.

Дисперсия выходного параметра у:

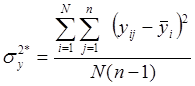
Дисперсия среднего значения выходного параметра (дисперсия воспроизводимости):

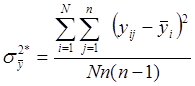.                                                         (5)

Проверка значимости коэффициентов регрессии. Значимость коэффициентов регрессии проверяется в сопоставлении их абсолютной величины с ошибками эксперимента. Считается, что коэффициент значим, если его абсолютная величина

|b_k| > Δb_k, где Δb_k - ошибка при его определении, рассчитываемая по выражению:

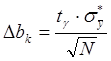.                                                              (6)

Квантиль t_γ находится в зависимости от числа степеней свободы f=п-1 и доверительной вероятности γ по таблицам.

Выполнение работы.

Эксперимент лабораторной работы заключается в нагревании резисторов. Пять резисторов нагрели до температур 20, 40 и 60 градусов в термошкафу и измерили их сопротивление с помощью электронного омметра. Измеренные результаты представлены ниже в таблице. По измеренным значениям были рассчитаны средние значения сопротивлений, которые также приведены в таблице.

Температура	Сопротивление, Ом
	R1	R2	R3	R4	R5	Rсреднее
20	109,4	109,5	110,9	110,4	107,5	109,54
40	109,3	109,4	110,8	110,3	107,4	109,44
60	109	109,2	110,7	110,1	107,3	109,26

Далее по методу наименьших квадратов определяются коэффициенты  и α линейной зависимости , где - начальная температура, а - начальное сопротивление резистора. Допустим, что , , ,, , а  – число значений , равно 3.

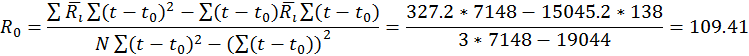
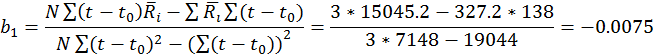
Тогда зависимость сопротивления от температуры выглядит следующим образом:

, и представлена ниже на графике.

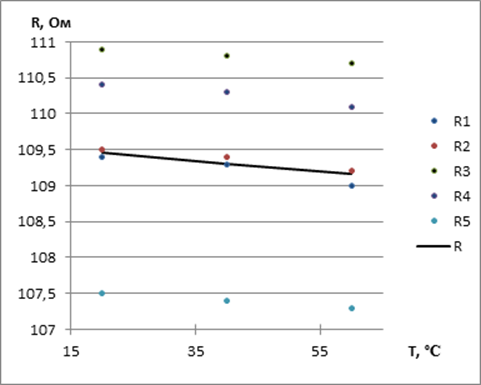
Рис.2 График зависимости сопротивления от температуры

Далее с помощью критерия Фишера надо проверить адекватность математической модели:

 и  - число степеней свободы.

Находим дисперсию адекватности

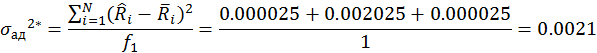
Находим дисперсию воиспроизводимости (n=5 – число параллельных опытов).

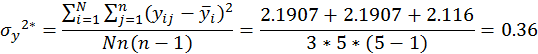
Находим

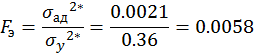
По таблице находим значение критерия Фишера при  и  и уровнях значимости: ; ;  - модель адекватна.

Далее проверяем значимость коэффициентов регрессии  и .

Число степеней равняется

Ищем ошибки при определении коэффициентов при доверительной вероятности ; квантиль распределения Стьюдента

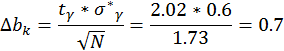
 – коэффициент значим

 – коэффициент не значим

Коэффициенты зависимости R(t)		Значимость коэффициентов bi		Дисперсия адекватности	Дисперсия воспроизводимости
				0,0913	0,4795

Вывод: в результате проведения и выполнения лабораторной работы построена математическая модель процесса изменения сопротивления резисторов от температуры при помощи пассивного эксперимента. Получившаяся модель оказалась адекватной и была построена на основе линейной зависимости по методу наименьших квадратов. Расхождения результатов опытов со значениями, которые были получены из модели, не превышают пары процентов. Из уравнения зависимости один коэффициент оказался мало значим, это объясняется тем, что у него относительно малое значение по сравнению с ошибкой эксперимента. Чтобы более точно определить значимости коэффициентов модели, нужно увеличить число параллельных опытов и количества различных значений температур.