можно считать величиной постоянной и равной r, то есть радиальной координате до точки наблюдения.
Таким образом:
|
|
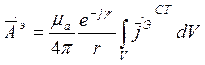 (2)
(2)
В (2) интегрирование осуществляется по
объему, занимаемому ЭЭИ. На первый взгляд интеграл в выражении (2)
должен вызывать некоторые трудности, так как интегрирование осуществляется по
исчезающе малому объему. Это преодолевают, анализируя размерность данного
интеграла 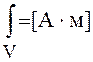 .
.
Учитывая, что в ЭЭИ амплитуду тока можно считать практически равномерной, а интегрирование по объему вырождается в интегрирование по длине, размерность интеграла соблюдается, если он равен:
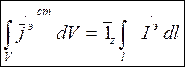 (3)
(3)
Векторный электрический потенциал в точке наблюдения будет равен:
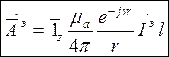 (4)
(4)
где ![]() - уравнение для
сферической волны, расходящейся от начала координат.
- уравнение для
сферической волны, расходящейся от начала координат.
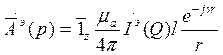
Полученный векторный электрический потенциал совпадает по направлению с током, протекающим по ЭЭИ. Разложим векторный электрический потенциал по координатам сферической системы
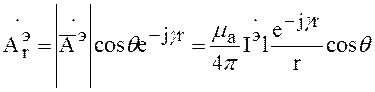 (5)
(5)
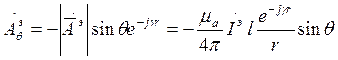 (6)
(6)
Так как проекция вектора ![]() на
плоскость угла равна 0 , то
на
плоскость угла равна 0 , то 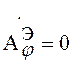 (7)
(7)
Внешняя электродинамическая задача. Задача считается, когда по полю векторного электрического потенциала определяют соответствующие электромагнитные составляющие поля. Уравнения связи имеют следующий вид:
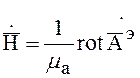 (1)
(1)
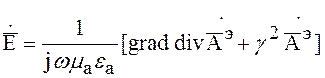 (2)
(2)
 (3)
(3)
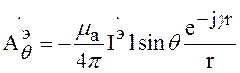 (4)
(4)
Запишем проекции ротора этих величин в сферических координатах:
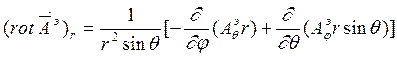
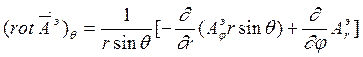
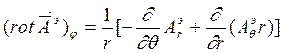
Задача вычисления
электромагнитного поля существенно упрощается, так как ![]() ,
оставшиеся проекции не зависят от угла j
и
,
оставшиеся проекции не зависят от угла j
и 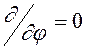 . Таким образом, в этом случае:
. Таким образом, в этом случае:
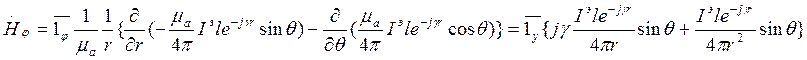
Магнитное поле в любой точке пространства:
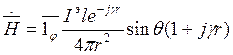 (5)
(5)
Теперь определим электрическое поле:
для этого воспользуемся первым уравнением Максвелла:
![]()
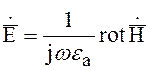
Представим, что вместо А в соотношениях (для rotA)
стоит Н, так как уравнения сходны (см.выше![]() ):
):
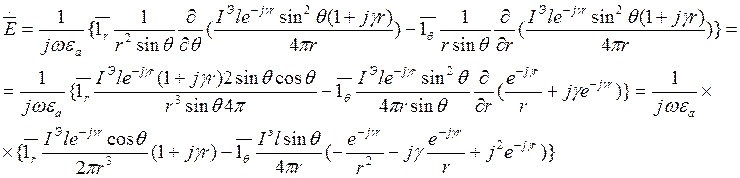
Элементарная проекция электрического поля для ЭЭИ:
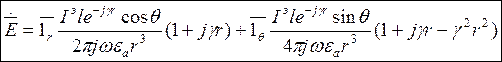
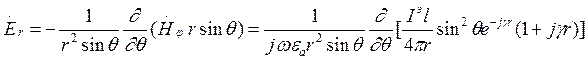
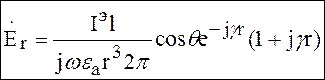 (6)
(6)
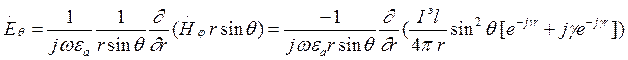
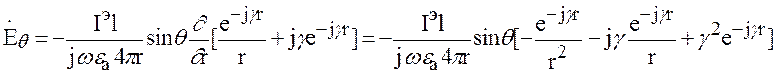
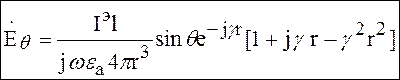 (7)
(7)
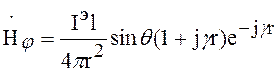
|
|
|
|
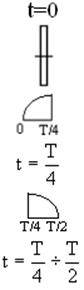 Полученные соотношения позволяют построить структуру поля
в свободном пространстве, то есть в любой области на любом расстоянии от
излучателя. Используя эти соотношения для ряда дискретных значений времени,
построим качественно структуру электрического поля.
Полученные соотношения позволяют построить структуру поля
в свободном пространстве, то есть в любой области на любом расстоянии от
излучателя. Используя эти соотношения для ряда дискретных значений времени,
построим качественно структуру электрического поля.
Пусть ток протекает снизу вверх, тогда к концу промежутка верхняя часть зарядится “+”, нижняя “-”.
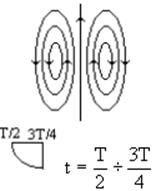
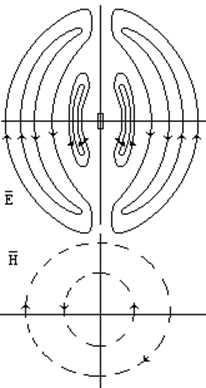 Переменный ток
начинает убывать. Начинается процесс “отшнуривания” силовых линий
электрического поля. К концу этой четверти периода электрический ток равен 0,
процесс “отшнуривания” завершается полностью, т. е. электрическое поле не
связано с поверхностью ЭЭИ.
Переменный ток
начинает убывать. Начинается процесс “отшнуривания” силовых линий
электрического поля. К концу этой четверти периода электрический ток равен 0,
процесс “отшнуривания” завершается полностью, т. е. электрическое поле не
связано с поверхностью ЭЭИ.
Ток протекает сверху вниз. Нижняя часть заряжается “+”, верхняя “-”.
Для некоторого
дискретного момента времени зарисуем структуру поля. Анализируя полученные в
предыдущем параграфе соотношения, можно отметить следующее: свойства 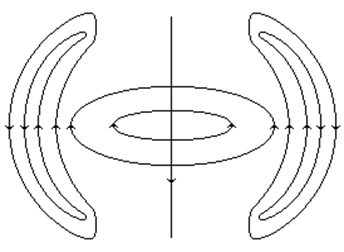 электромагнитного
поля возбуждаемого ЭЭИ, в непосредственном его окружении довольно различны, при
значительном удалении. При
электромагнитного
поля возбуждаемого ЭЭИ, в непосредственном его окружении довольно различны, при
значительном удалении. При ![]() , то есть в
непосредственном окружении, основной смысл в выражениях имеют слагаемые,
зависящие от расстояния — 1/r3, 1/r2. Слагаемые,
зависящие от 1/r, делают очень маленький вклад. При
, то есть в
непосредственном окружении, основной смысл в выражениях имеют слагаемые,
зависящие от расстояния — 1/r3, 1/r2. Слагаемые,
зависящие от 1/r, делают очень маленький вклад. При ![]() основной
вклад осуществляют составляющие, имеющие зависимость от расстояния — 1/r.
основной
вклад осуществляют составляющие, имеющие зависимость от расстояния — 1/r.
В связи с тем, что поля при ![]() и
при
и
при ![]() существенно отличаются, вводят понятия
ближней и дальней зоны ЭЭИ.
существенно отличаются, вводят понятия
ближней и дальней зоны ЭЭИ.
Ближнюю зону(БЗ) определяют правилом:
gr<<1 (1)
Дальнюю зону (ДЗ):
gr>>1 (2)
Очевидно, что точной границы между ними не существует.
Рассмотрим свойства электромагнитного поля в ближней и дальней зонах.
В БЗ поле имеет преимущественно реактивный характер. Говорят, что в БЗ поле является квазистатическим, подчеркивая этим самым, что в БЗ поле сохраняется и даже частота возбуждающего тока стремится к 0. В БЗ существуют все 3 компоненты Е q, Еr, Нj. Амплитуда поля в БЗ быстро затухает с удалением от ЭЭИ.
В ДЗ (зона излучения) компоненты поля синфазны, что свидетельствует об активном характере электромагнитного поля. Еr пренебрежимо мала по сравнению с Е q. Вектор П чисто активен и параллелен радиальной координате, то есть
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.