Форма кривых напряжения и тока, страница 2

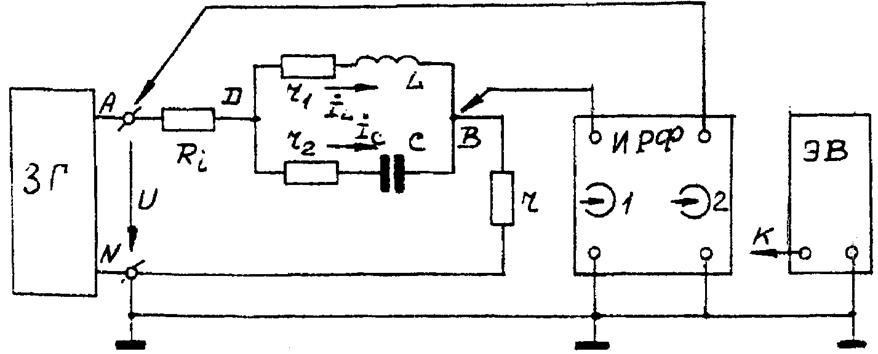
3.2.4. Исследование АЧХ. Включить последовательно с параллельным контуром сопротивление R_i>>R₀  (R₀ -входное сопротивление параллельного контура на резонансной частоте). Снять зависимости I=F(f), U_c=F(f), изменяя частоты выше и ниже резонансной. Данные эксперимента занести в табл. 14.4. Схема на рис. 14.3.

4. Обработка. результатов измерений _________________

4.1. Расчет частотных характеристик при последовательном соединении

4.1.1. Для схемы на рис. 14.1, пользуясь данными опыта п. 3.1.3 , рассчитать резонансный ток I₀ и отношение тока в цепи для других частот к току при резонансе I/I₀ , вычислить входное сопротивление цепи _вх,X, мощность и коэффициент мощности. Результаты расчета занести в табл. 14.2.

4.1.2. Пользуясь результатами расчета п. 4.1.1, построитьамплитудно-частотные и фазочастотные характеристики, кривую I/I₀=F(f).

4.1.3. По графикам п. 4.1.2 и п. 3.1.4 определить полосу пропускания, затухания и величину добротности контура (двумя способами) без добавочного сопротивления и с ним.

4.1.4. Рассчитать максимальное значение энергии индуктивности и емкости при резонансе и сравнитьих.

4.1.5. Пользуясь результатами п. 3.1.5 для новой добротности, рассчитать резонансный ток I₀ и отношение I/I₀, входное сопротивление _вх и занести в таблицу, составленную в п. 3.1.5.

4.1.6. Построить векторные диаграммы для трех случаев по данным п. 4.1.1: при резонансе, до и после резонанса.

4.2. Расчет частотных характеристик при параллельном соединении.

4.2.1. Для схемы, изображенной на рис. 14.2, пользуясь данными опыта п. 3.2.3, рассчитать токи в параллельных ветвях, проводимости Y,b_L,b_c, мощность и коэффициент мощности. Результаты расчета занести в табл. 14.3.

4.2.2. Пользуясь результатами расчета п. 4.2.1, построить зависимости I_c=F(f); I_L=F(f); I=F(f); Y=F(f); b=F(f); P=F(f); Q=F(f); cosj=F(f); j=F(f).

4.2.3. Построить векторные диаграммы для трех случаев по данным п. 4.2.1: при резонансе, до и после резонанса.

4.2.4. Рассчитать максимальное значение энергии индуктивности и емкости при резонансе и сравнитьих.

4.2.5 Пользуясь данными п. 4.2.1, рассчитать активное сопротивление катушки r_k. Рассчитать эквивалентную добротность с учетом сопротивления катушки.

4.2.6. Пользуясь данными п. 4.2.1 и значением добротностиконтура при резонансе, рассчитать напряжение на индуктивности и емкости при резонансе и сравнить полученные результаты с опытными.

4.3. Анализ полученных данных

Дать критическое сравнение резонансов напряжения и токов, выделить особенности каждого резонанса, достоинства и недостатки, резать области применения режимов резонанса.

5. Учебно-исследовательная работа_________________

5.1. При заданной величине индуктивности L= 25 мГц рассчитать величину емкости для получениярежима резонанса напряжения при частоте f₀=2,5 кГц. Проверить полученные расчеты экспериментально.

5.2. Рассчитать величину индуктивности для режима резонанса тока при заданной емкости С=0,2мкФ и резонансной частоте f₀= 4 кГн. Повторить расчеты с учетом активных сопротивлений r₁ и r₂ параллельных ветвях. Проверить полученные данные расчета экспериментально.

5.3. Рассчитать значения сопротивлений r₁, r₂ для случая, когда резонансная частота при параллельном и последовательном соединении одинакова. Установить эти сопротивления в схему и проверить экспериментально.

5.4. Подобрать для параллельного соединения такие сопротивления, чтобы цепь резонировала на любой частоте.

5.5. Подобрать для параллельного соединения такие сопротивления, чтобы явление резонанса не возникало.

6. Методические указания__________________

Резонанс напряжения - это режим цепи при последовательном включении r-L-C , при котором входное реактивное сопротивление цепи равно нулю.

Резонанс напряжений характеризуется следующими соотношениями;

1.  Ток в цепимаксимальный

I₀=U/Z₀=U/r=I_max

2. Действующие значения напряжений на индуктивности и емкости равны и могут превышать напряжение сети, так как сопротивления реактивных элементов равны и могут превышать активное сопротивление

X_L=X_c>>r;  I₀X_L=I₀X_c>>U.

3. Напряжение сети приложено к активному сопротивлению

U_сети=I₀r=U_r.

4. Реактивная мощность цепи равна нулю

Q₀=Q_L-Q_C=I(x_L-x_c)=0.

5. Резонансная частота цепи определяется из равенства нулю его реактивного сопротивления.

w_nL-1/(w₀C)=0 ® f₀=1/(2p)

6. Реактивное сопротивление определяется разностью максимальных значений энергии, запасаемой в магнитном и электрическом полях