






Содержание
1. Задание на расчёт……………………………………………………….3
2. Коэффициент передачи , АЧХ и ФЧХ цепи…………………………..4
3. Импульсная и переходная характеристики цепи……………………..5
4. Разложение периодического сигнала в ряд Фурье……………………6
5. Отклик цепи на периодический сигнал ……………………………….9
6. АЧХ и ФЧХ непериодического сигнала ………………………………10
7. Отклик цепи на непериодический сигнал…………………………….12
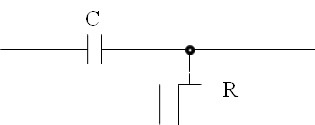
1. Задание
 |
|||
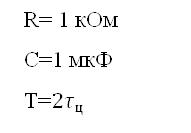 |
|||
![]()
![]()
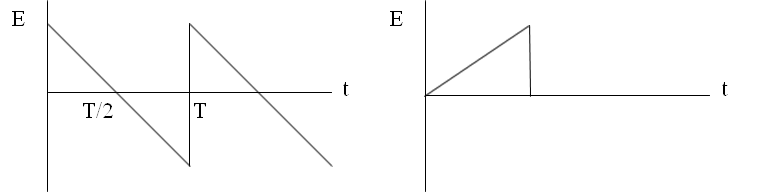
Периодический сигнал Непериодический сигнал
 |
τ
1) Рассчитать и построить графики следующих характеристик цепи:
амплитудно-частотная характеристика;
фазо-частотная характеристика;
импульсная характеристика;
переходная характеристика.
2) Для периодического сигнала найти разложение в ряд Фурье. Просуммировать на периоде первые пять членов этого ряда. Построить соответствующие графики.
3) Для непериодического сигнала найти выражение для спектральной плотности. Построить АЧХ и ФЧХ.
4) Найти отклик цепи на периодический сигнал, для этого записать выражение ряда Фурье для сигнала на выходе цепи и просуммировать первые пять членов. Построить соответствующие графики.
5) Найти отклик цепи на непериодический сигнал. Построить соответствующие графики.
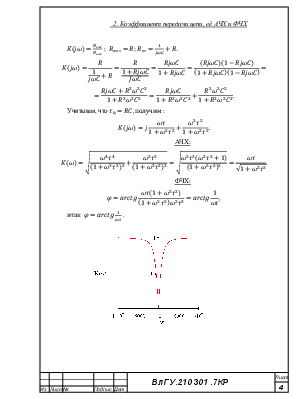
2. Коэффициент передачи цепи, её АЧХ и ФЧХ
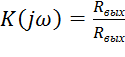 ;
; ![]() ;
; 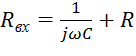 .
.
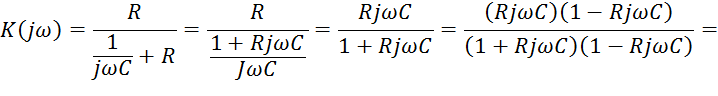
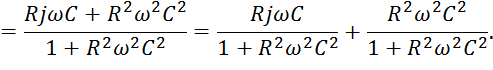
Учитывая, что ![]() :
:
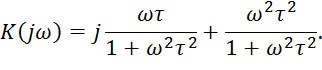
АЧХ:
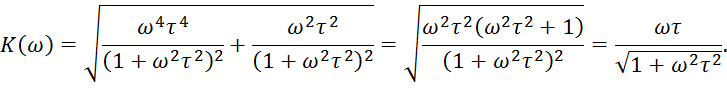
ФЧХ:
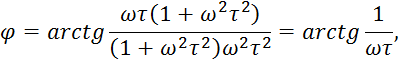
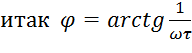 .
.
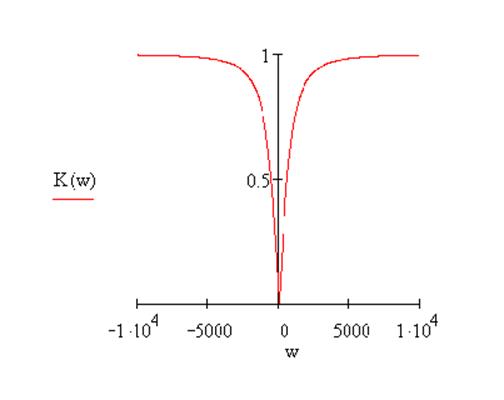
Графики:
АЧХ:
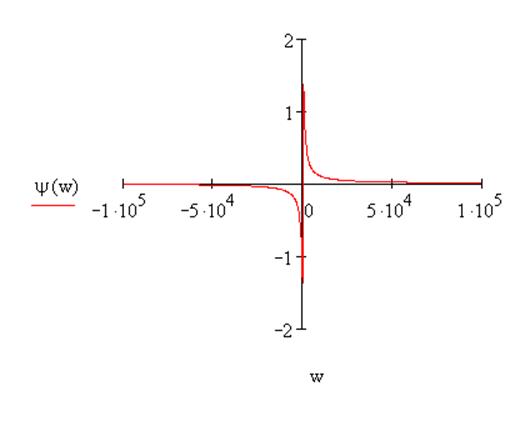 ФЧХ:
ФЧХ:
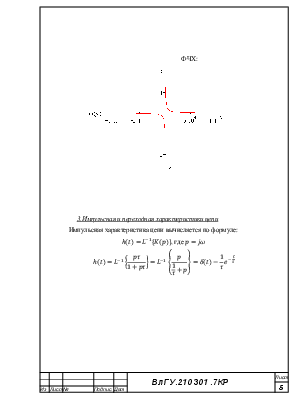
3.Импульсная и переходная характеристики цепи
Импульсная характеристика цепи вычисляется по формуле:
![]() , где
, где ![]()
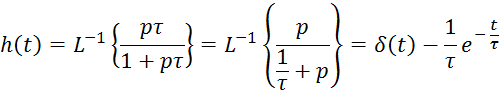
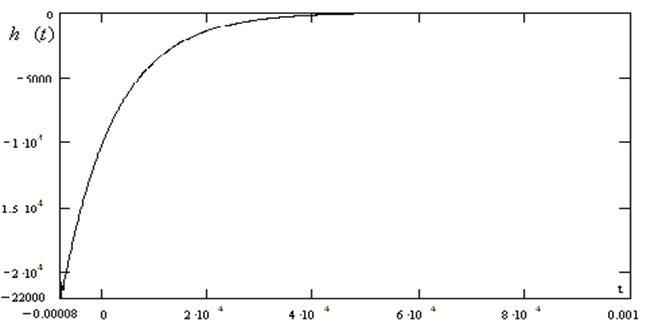
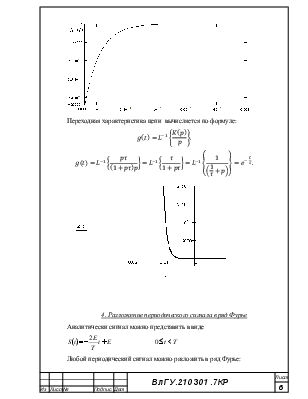
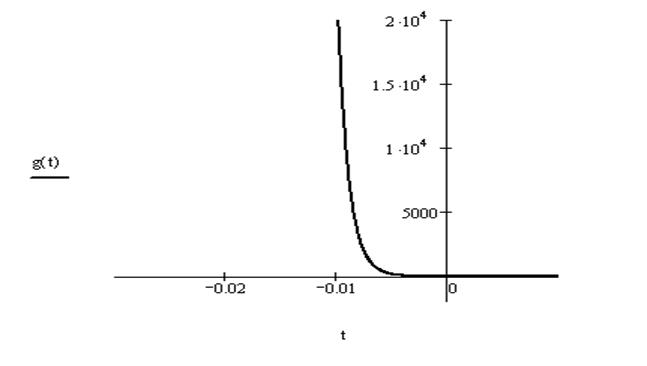
Переходная характеристика цепи вычисляется по формуле:
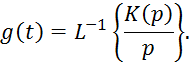
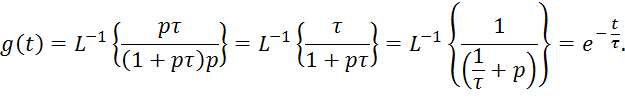
4. Разложение периодического сигнала в ряд Фурье
Аналитически сигнал можно представить в виде
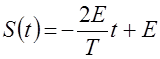
![]()
Любой периодический сигнал можно разложить в ряд Фурье:
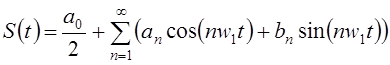
Вычислим коэффициенты ряда:
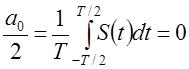 ,
,
так как интеграл от нечетной функции в симметричных пределах равен нулю.
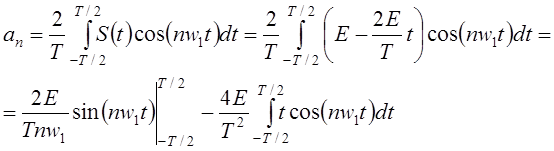
Последний интеграл найдём отдельно:
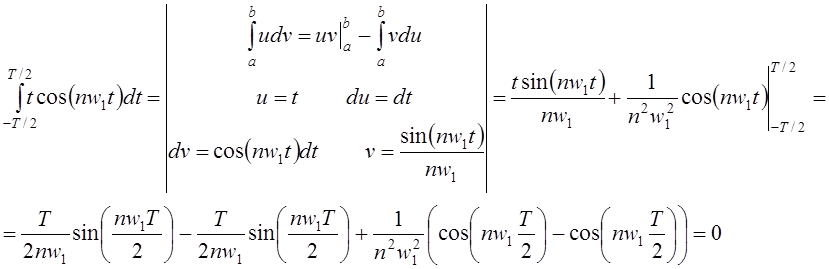
Тогда :
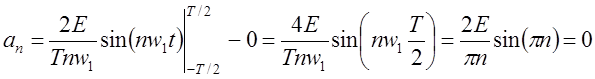
Такой же вывод можно было сделать из условия нечётности периодического сигнала.
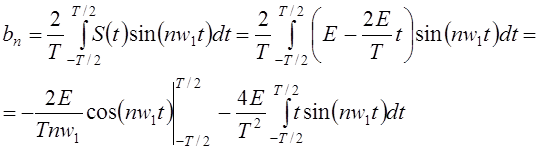
Последний интеграл найдём отдельно:
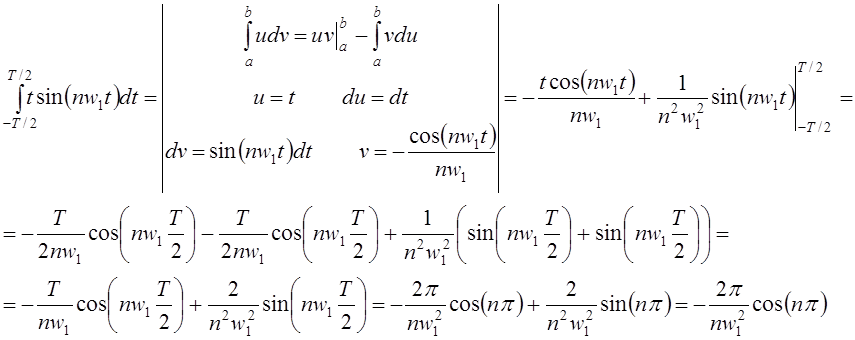 Тогда:
Тогда:
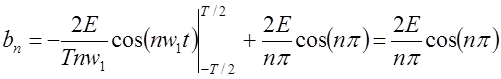
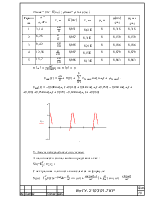
Вычислим первые пять членов ряда:
![]()
![]()
![]()
![]()
![]()
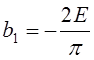
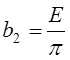
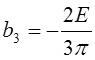
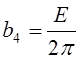
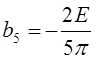
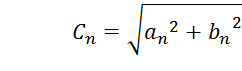 ;
; ![]() -
-![]() ;
; 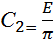 ;
; ![]() -
-![]() ;
; 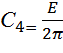 ;
; ![]() -
-![]() .
.
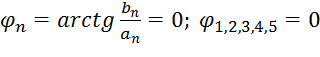
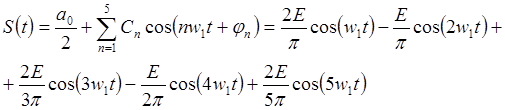
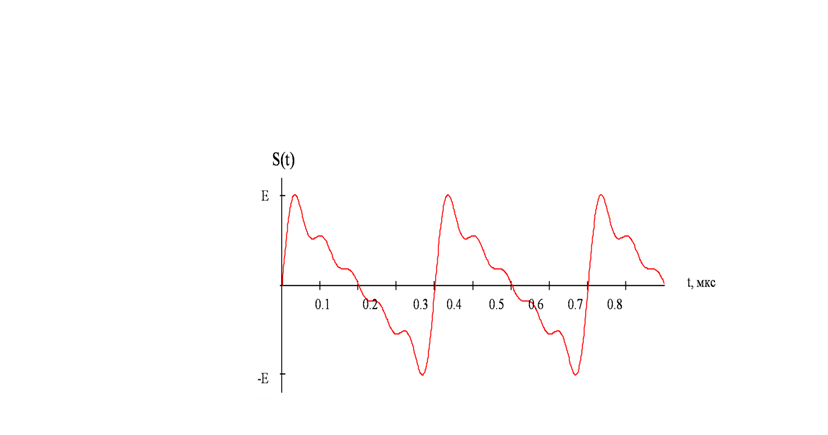
Отклик цепи на периодический сигнал
Для вычисления отклика цепи на периодический сигнал, необходимо амплитуду каждой гармоники входного сигнала домножить на значение АЧХ на соответствующей частоте, а к фазе гармоник добавить значение ФЧХ на этой частоте. И просуммировать гармоники.
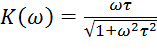 ;
; 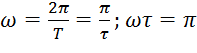
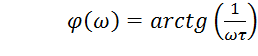
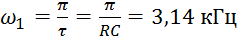 .
.
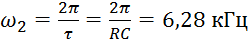 .
.
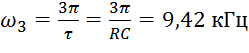
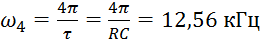
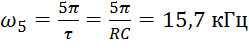
![]() =
=![]() * K(nω) ;
* K(nω) ; ![]() =
= ![]() + φ(nω)
+ φ(nω)
|
Гармоника |
|
|
|
|
|
|
|
|
1 |
3,14 |
- |
0,951 |
-0,61E |
0 |
0,318 |
0,318 |
|
2 |
6,28 |
|
0,987 |
0,31E |
0 |
0,159 |
0,159 |
|
3 |
9,42 |
- |
0,995 |
-0,21E |
0 |
0,106 |
0,106 |
|
4 |
12,56 |
|
0,997 |
0,15E |
0 |
0,079 |
0,079 |
|
5 |
15,7 |
- |
0,998 |
-0,13E |
0 |
0,063 |
0,063 |
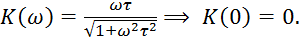
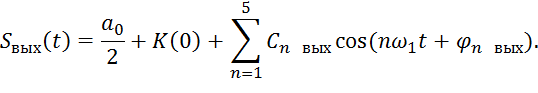
![]()
![]()
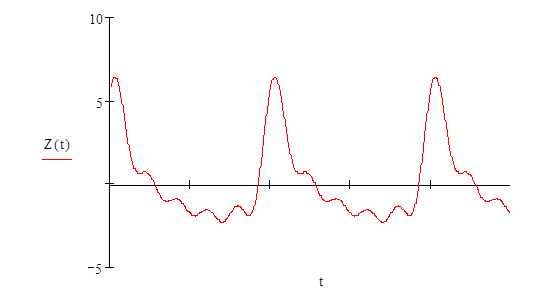
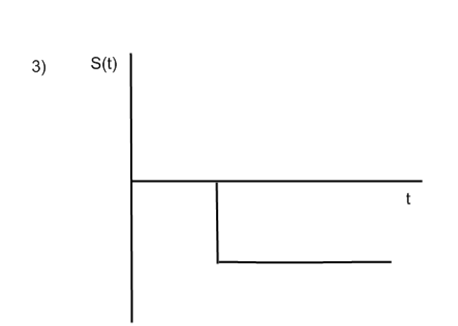
5. Анализ непериодического сигнала
Аналитически сигнал можно представить как :
S(t)=E![]() ; 0≤ t≤ τ
; 0≤ t≤ τ
Спектральная плотность вычисляется по формуле:
S(jω)= ![]() dt =
dt = ![]() [ sin (ωτ) +
[ sin (ωτ) + 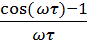 ] + j
] + j![]() [ cos(ωτ) –
[ cos(ωτ) – 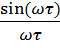
АЧХ: 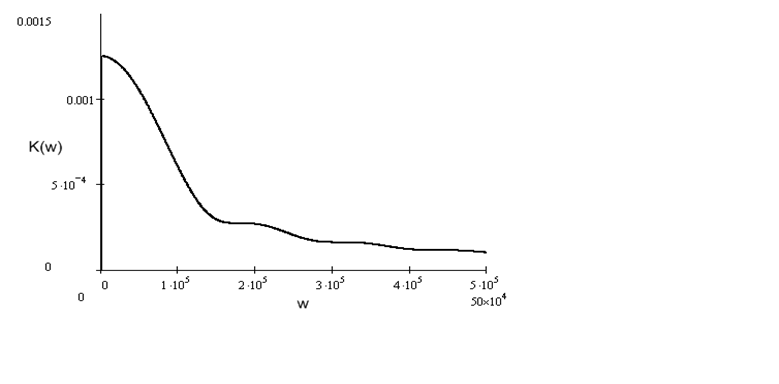
ФЧХ: 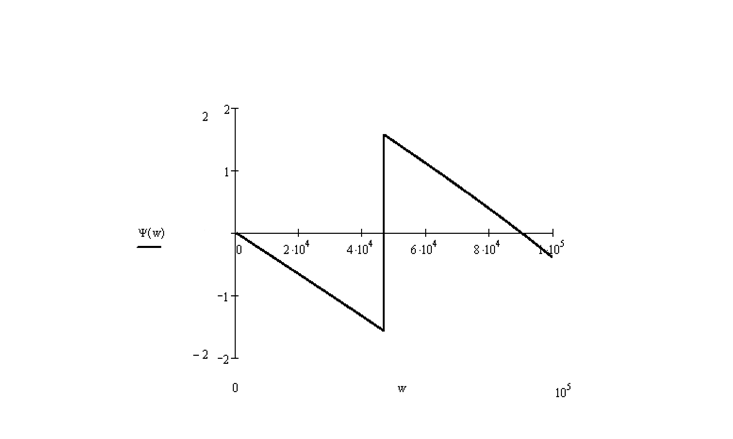
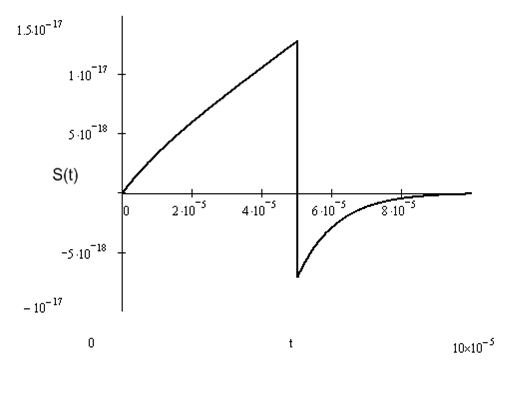
Отклик цепи на непериодический сигнал
Отклик цепи на непериодический сигнал можно вычислить с помощью обратного преобразования Лапласа от произведения спектральной плотности сигнала на коэффициент передачи цепи.
![]()
Представим наш сигнал как сумму: 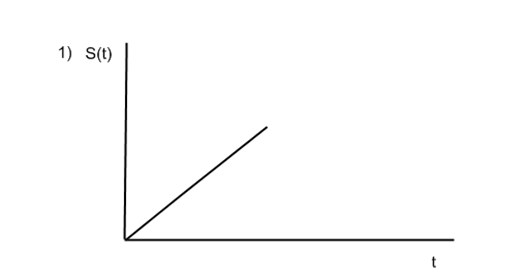
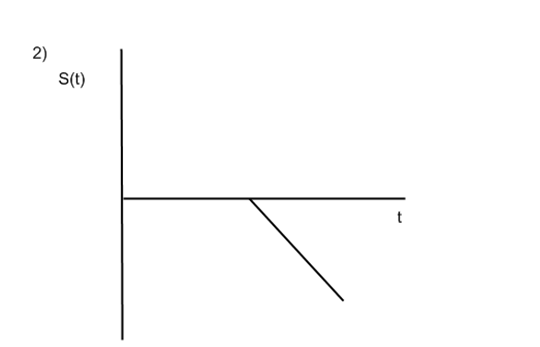
![]() (p) =
(p) =![]() ;
; 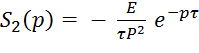 ;
; 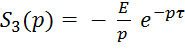
S(p) = ![]() =
=
![]() (
(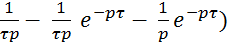
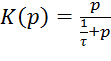
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.