Исследование влияния дестабилизирующих факторов на параметры выпускаемых изделий

Федеральное агентство по образованию РФ

Государственное образовательное учреждение высшего профессионального образования

"Владимирский государственный университет"

Кафедра КТРЭС

Лабораторная работа № 3

Исследование  влияния  дестабилизирующих факторов

на параметры выпускаемых изделий

Вариант № 16

Выполнил: ст.гр. Р-107

Проверил:

Владимир, 2010

Цель работы: Изучение  методики  дисперсного  анализа.

Исходные данные.

ряд 1: 499,505,522,481,512,494,466,489,497,515,464,515,501,532,505,496,452,505,512,493,490,506,496,482,496,500,489,515,505,494,527,503,510,506,484,532,486,499,506,465,519,530,495,498,480,515,519,516,473,487.

ряд 2: 507,511,528,491,505,500,504,500,529,530,528,541,498,512,557,525,531,563,539,546,546,542,509,516,546,543,546,572,550,575,537,597,571,578,569,583,567,611,574,581,559,578,603,608,562,583,575,587,602,593.

ряд 3: 607,630,556,603,616,576,573,604,585,573,575,582,609,587,574,586,612,566,562,553,549,546,564,567,560,554,523,512,538,534,530,532,545,570,542,526,507,560,524,512,497,513,528,533,495,499,505,483,518,469.

Ряд 1: , , .

Ряд 2: , , .

Ряд 3: , , .

Объем выборки n = 50, число выборок m = 3.

Ход работы.

Для  каждого  уровня  наблюдений  вычисляется частная  средняя    и  частная  статистическая  дисперсия    (i=1,2,…m)  и  результаты  заносятся в  таблицу 1.

Таблица 1 – Результаты наблюдений

Общая  средняя  арифметическая  и  общая  статистическая  дисперсия вычисляются по формулам

,

.

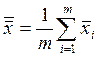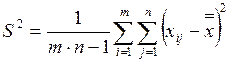После подстановки чисел общая средняя и общая дисперсия получается равными

,

.

Межгрупповая  статистическая  дисперсия характеризует  разброс  средних  между  уровнями и вычисляется по формуле

.

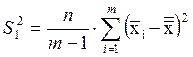Внутригрупповая  статистическая дисперсия, характеризующая разброс значений параметра внутри группы, вычисляется по формуле

.

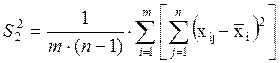После подстановки чисел межгрупповая статистическая  дисперсия получается равной

, а внутригрупповая статистическая дисперсия равной

.

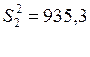Влияние внешнего фактора оценивают с помощью критерия Фишера. Расчетное значение критерия Фишера равно 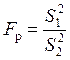. Табличное значение  находится по таблицам для заданного уровня значимости и степенях свободы  и .

При вероятности р = 0,95 и степенях свободы  и  критерий Фишера  равен . Расчетное значение критерия равно

.

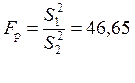Как нетрудно заметить, >, т.е. влияние исследуемого фактора на данный параметр качества продукции существенен.

Вывод: Для  оценки  влияния  производят  разложение  суммарной  выборочной  дисперсии  на  составляющие  дисперсии,  обусловленные  действием  независимых  факторов.  Чтобы  определить,  значимо  ли  влияние  данного  фактора,  необходимо  сравнить  соответствующую  выборочную  дисперсию  с  дисперсией  воспроизводимости,  обусловленной  действием  случайных  факторов.  Это сравнение  проводится  с помощью  критерия Фишера. В нашем случае расчетное значение равно , а табличное -  (при вероятности р = 0,95 и степенях свободы  и ). Как видно, >, что говорит о значимости исследуемого фактора на параметр качества продукции с вероятностью р = 0,95.