Уровень 2: Применить анализатор спектра для исследования спектров гармонического, импульсного (прямоугольного, треугольного и пилообразного), шумового и комбинированного сигнала.
Уровень 3: Изучить и освоить методики поверки анализатора спектрапутем определения его основных метрологических характеристик. Выполнить учебную поверку анализатора спектра (АС) с помощью образцовых виртуальных приборов.
2. Назначение и принципы работы АС
С помощью АС можно оценивать и измерять: стабильность частоты, чистоту спектральной линии; устойчивость к внешним факторам; параметры модуляции, ширину спектра частот; уровень паразитных составляющих; динамический диапазон; частотные характеристики; потери и нелинейность преобразования, развязку; подавление спектральных составляющих; искажения сигналов и др.
К функциям АС относятся абсолютное и относительное измерение частоты и уровня. Также АС обладает возможностью определения параметров шума и электромагнитной совместимости. Современные АС применяются при измерениях продуктов искажений и их побочных составляющих, сигналов с цифровой модуляцией и параметров АМ и ЧМ.
Основные характеристики АС:
- чувствительность 10-7…10-14 Вт;
- рабочий диапазон частот и полоса обзора (до десятков ГГц);
- разрешающая способность по f ;
Приборы можно разделить на следующие виды:
1. Аналоговые, использующие методы:
- фильтрации (последовательный или параллельный анализ);
- дисперсионные (или рециркуляционные).
2. Цифровые, использующие методы:
- сжатия временного масштаба;
- цифровой фильтрации и цифрового гетеродинирования;
- вычислительные на базе БПФ.
Преобразование Фурье позволяет представить сложный периодический процесс множеством простейших компонентов: гармонических колебаний со своими частотами, амплитудами и начальными фазами:
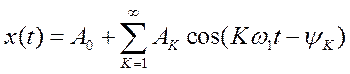
где А0 - постоянная составляющая сигнала; K - порядковый номер гармоники, АК- амплитуда K-ой гармоники; YК - начальная фаза K-ой гармоники; w1- частота первой (основной) гармоники.
Спектр периодического сигнала является дискретным или линейчатым. В общем случае периодический сигнал содержит постоянную составляющую и набор гармонических колебаний с частотами wK=Kw1, K=1,2,3…, кратными основной частоте w1.
Например, сигнал пилообразной формы может быть представлен суперпозицией бесконечного количества синусоидальных сигналов, частоты которых кратны основной частоте. Амплитуда и мощность этих синусоид уменьшаются с увеличением их частоты. По мере добавления каждой гармоники, форма сигнала становится более похожей на идеальную. Ряд Фурье пилообразного сигнала имеет вид:
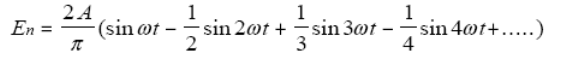 .
.
Идеальный сигнал прямоугольной формы включает в себя бесконечное количество нечетных гармоник. В таком случае ряд Фурье выглядит как:
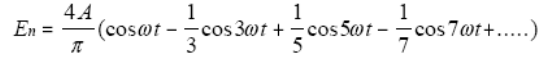
Так как амплитуда гармоник высоких порядков во много раз меньше амплитуды основной частоты, то, как правило, вычисляют ограниченное число гармоник (до 5-го … 9-го порядка).
Непериодические сигналы имеют непрерывный спектр,
т.е., в их составе присутствуют все частоты без исключения. Амплитуды отдельных
спектральных составляющих бесконечно малы, поэтому их спектральный состав
описывают не амплитудами отдельных гармоник, а спектральной плотностью, под
которой понимают отношение приращения амплитуды ![]() к
приращению частоты Dw на некоторой частоте.
к
приращению частоты Dw на некоторой частоте.
В виртуальном АС, используемом в лабораторных исследованиях, реализован вычислительный принцип оценки уровня и частоты
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.