Влияние особенностей каналов передачи на выбор методов обработки сигналов, страница 2

Характеристики многолучевости определяются свойствами создающих ее факторов:

- нестационарность или изменение по времени параметров, влияющих на многолучевость;

- изменение интенсивности их проявления или пространственное перемещение неоднородностей;

- групповое воздействие множества факторов или выраженное проявление определяющих факторов, что порождает либо непрерывную, либо дискретную многолучевость;

- изменение свойств принимаемого сигнала при перемещении приемника или передатчика в различных направлениях, а также изменение свойств при перемещении по частотной оси, изменении положения антенны при приеме/передаче и изменении поляризации.

Сигнал S_вх(t) в точке приема образуется сложением большого числа волн, пришедших по различным путям с задержками, (согласно точечной модели рассеяния). Для достаточно узкополосного излучаемого сигнала S_ВХ (t) сигнал на входе приемника будет

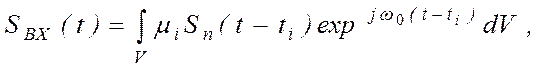
где V– объем, эффективно участвующий в переизлучении; m_i и t_i-  соответственно коэффициент отражения от i-той точки объема и время суммарной задержки при распространении сигнала от передатчика до i-той точки и далее до приемника;  – центральная частота излучаемого узкополосного сигнала.

Обычно предполагается, что переотражающая способность m_i  мало зависит от частоты в достаточно широком диапазоне. Также не учитываются переходные процессы в канале, обусловленные его дисперсионными свойствами.

При анализе ионосферных и тропосферных каналов в течение длительного времени величину μ следует считать нестационарным случайным процессом. Однако, на небольших интервалах времени (порядка нескольких минут) нестационарностью можно пренебречь, процесс изменения μ можно полагать локально-стационарным, а его статистические характеристики – неизменными. Такие изменения передаточной функции канала принято называть быстрыми замираниями.

Известны различные модели, описывающие процессы быстрых замираний, которые основаны на этом подходе и порождают соответствующие распределения (например, рэлеевское распределение, m–распределение Накагами, четырехпараметрическое распределение и др. Большую часть времени сеансов связи наблюдается рэлеевское распределение замираний, однако более общей моделью является четырехпараметрическая модель. Существуют и другие модели каналов. Интенсивность каждого элемента m_i  представляет собой случайную величину. В таких условиях выполняется центральная предельная теорема, и компоненты m_i можно считать распределенному по гауссову закону с некоторыми средними m_C и m_S  и дисперсиями s_S² и s_C²

Однако, откладывая m_C и m_S вдоль осей OX и OY некоторой координатной плоскости и поворачивая систему координат на нужный угол, можно перейти к совместной плоскости распределения некоторых двух новых независимых величин C и S

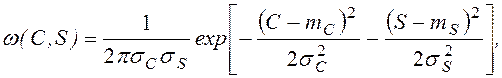где m_C, m_S, s_C и s_S – новые параметры двух гауссовых распределений величин C и S, полученных после поворота. Поворот не меняет распределение модуля μ=|m|

Подобная четырехпараметрическая модель достаточно хорошо описывает результат интерференции радиоволн на входе приемника, отраженных от распределенных по объему V переизлучателей, в том числе при наличии достаточно интенсивной регулярной компоненты. Различные сочетания значений данных четырех параметров соответствуют различным характерным частным случаям.

Например, в случае, когда m_c=m_s=0; s_С=s_S=s , имеет место релеевское распределение модуля коэффициента передачи

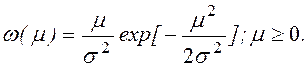При наличии большой регулярной компоненты m_c=m_s≠0; s_C=s_S=s наблюдается обобщенное рэлеевское распределение (распределение Рэлея-Райса)

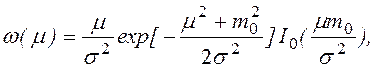где I₀(z)- модифицированная функция Бесселя первого рода нулевого порядка.

Интерференция обуславливает быстрые замирания амплитуды сигнала, спектр которых лежит в интервале от долей герца до десятков герц. С этими величинами соизмеримы колебания фазового сдвига (аргумента величины μ). Распределение arg(μ) равномерно в интервале 0¸2π в случае рэлеевского распределения амплитуды. В других вариантах четырехпараметрической модели распределение фазы несимметрично и может иметь несколько экстремумов.