




































Системы счисления. Перевод чисел из одной системы счисления в другую.
Совокупность приемов наименования и записи чисел называется счислением.Под системой счисления понимается способ представления любого числа с помощью ограниченного алфавита символов, называемых цифрами Счисление представляет собой частный случай кодирования, где слово, записанное с использованием определенного алфавита и по определенным правилам, называется кодом. Применительно к счислению это - код числа.
Различают:
- непозиционныесистемы счисления (например, римская), где в любом месте числа каждой цифре соответствует одно и то же значение;
- позиционныесистемы счисления, где одна и та же цифра имеет разное значение, которое определяется ее позицией в последовательности цифр, изображающей число. Количество символов S, употребляемое в позиционной системе счисления, называется ее основанием. Позиционной является десятичная (D - decimal) система счисления, для которой S = 10, а для записи используется алфавит из 10 цифр (0,1,2,..., 9).
В позиционной системе счисления каноническая форма представления числа Xsвыглядит следующим образом:
|
Х10 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Х2 |
0 |
1 |
10 |
11 |
100 |
101 |
110 |
111 |
1000 |
1001 |
|
Х8 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
10 |
11 |
|
Х16 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Х10 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
Х2 |
1010 |
1011 |
1100 |
1101 |
1110 |
1111 |
10000 |
10001 |
10010 |
10011 |
|
Х8 |
12 |
13 |
14 |
15 |
16 |
17 |
20 |
21 |
22 |
23 |
|
Х16 |
A |
B |
C |
D |
E |
F |
10 |
11 |
12 |
13 |
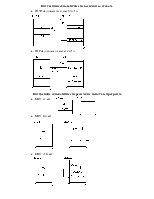
Цифровые вычислительные устройства используют также системы счисления с недесятичным основанием: двоичная, восьмеричная и шестнадцатеричная. Наиболее сжатая получается запись в шестнадцатеричной системе счисления, а наибольшего числа разрядов требует двоичное представление числа. Следует вместе с тем отметить, что ЦВУ (ЭВМ) воспринимает информацию только в виде двоичных кодов.
Наряду с двоичными кодами, которыми оперирует ЦВУ, для ввода и вывода десятичных чисел используют специальное двоично-десятичное кодирование, при котором каждая десятичная цифра заменяется тетрадой двоичных цифр, а сами тетрады записываются последовательно в соответствии с порядком следования десятичных цифр. При обратном преобразовании двоично-десятичного кода в десятичный исходный код разбивается на тетрады вправо и влево от запятой, которые затем заменяются десятичными цифрами.
При двоично-десятичном кодировании фактически не производится перевод числа в новую систему счисления, а используется двоично-кодированная десятичная система счисления.
Пример:десятичное число 9510 = 1001 01012.10.
ЦВУ работают с двоичными кодами, пользователю удобнее иметь дело с десятичными или шестнадцатеричными, поэтому возникает необходимость перевода числа из одной системы счисления в другую.
Пример: перевести целое число Х10=56 в двоичную систему счисления.
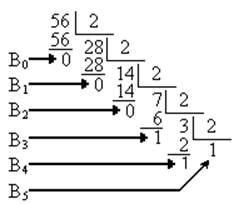
Х2=111000
Проверка: Х10=32+16+8+0+0+0=56
Для перевода из двоичной
в восьмеричную или шестнадцатеричную систему счисления необходимо в двоичной записи числа
произвести разбиение на
триады (тетрады), после
чего заменить каждую триаду (тетраду) двоичных символов ее эквивалентом в соответствующей системе
счисления.В обратных преобразованиях (![]() и
и ![]() ) следует
просто заменить символы в записи числа на их двоичные эквиваленты (см.
таблицу):
) следует
просто заменить символы в записи числа на их двоичные эквиваленты (см.
таблицу):
![]()
Преобразования
![]() и
и ![]() проще производить с промежуточным использованием двоичной записи.
проще производить с промежуточным использованием двоичной записи.
Формы представления цифровой информации.
Бит – одноразрядное двоичное число (1 бит).
Тетрада (нибл, полубайт) – четырехразрядное двоичное число (4 бита).
Байт – восьмиразрядное двоичное число (8 бит).
Слово – шестнадцатиразрядное двоичное число (2 байта, 16 бит) [дополнительно зависит от устройства].
Также используются понятия: двойное слово (2 слова), килобайт (210 байт
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.