Разработка математической модели и оптимизации параметров узла РЭА

Федеральное агентство по образованию Российской Федерации

Государственное образовательное учреждение

высшего профессионального образования

Владимирский государственный университет

Кафедра конструирования и технологии радиоэлектронных средств

лабораторная работа 5

«разработка математической модели и оптимизации параметров узла РЭА»

по дисциплине: «Математические основы проектирования электронных средств»

Выполнил:

студент гр. Р-105

Руководитель:

Владимир 2007

Цель работы: изучить методику планирования эксперимента, составить математическую модель узла РЭА и оптимизировать его параметры.

1 Планирование

Для получения уравнения регрессии первой степени достаточно варьировать факторы на двух уровнях. Для факторов, имеющих два уровня, верхний уровень обозначается +1, а нижний -1; порядок уровней не имеет значения.акладываются ограничения сверху и снизу.

На выбор интервалов накладываются ограничении я сверху и снизу. Интервал варьирования не может быть меньше той ошибки, с которой экспериментатор фиксирует уровень фактора. Интервал не может быть настолько большим, чтобы верхний и нижний уровни оказались за пределами области определения.

Размер интервала варьирования составляет некоторую долю от области определения фактора. Если интервал не более 10% от области определения, то считается узким, а до 30% - широким.

Таблица 1. Условия линейного факторного эксперимента.

Фактор	Нулевой уровень фактора	Шаг варьирования	Уровень фактора
			-1	+1
R1	3·105 Ом	15%	3·105-15%	3·105+15%
R2	7,5·103 Ом	15%	7,5·103-15%	7,5·103+15%
R3	5,6·103 Ом	15%	5,6·103-15%	5,6·103+15%

Матрица ортогонального планирования задается в виде совокупности +1 и -1, под которыми понимаются соответственно верхний и нижний уровни параметра.

Таблица 2. Матрица планирования.

№п/п	R0	R1	R2	R3	R1R2	R2R3	R1R3	Uвых
1	+	-	-	+	+	-	-	U1
2	+	-	+	-	-	-	+	U2
3	+	+	-	-	-	+	-	U3
4	+	+	+	+	+	+	+	U4
5	+	-	-	-	+	+	+	U5
6	+	-	+	+	-	+	-	U6
7	+	+	-	+	-	-	+	U7
8	+	+	+	-	+	-	-	U8

В таблице 2 R₀ – фиктивная переменная, служащая для определения b₀ в уравнении регрессии. Это значит, что в первом опыте две переменные берутся на нижнем уровне, а третья – на верхнем уровне и т.д. фиктивная переменная R₀ всегда принимает значение +1.

Матрица планирования должна удовлетворять следующим требованиям:

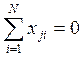 - условие симметричности плана,

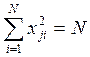 - условие нормирования,

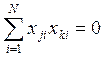 - условие ортогональности, где N – число опытов,

i – индекс номера,

j – индекс столбца

2 Проведение эксперимента

Таблица 3. Результат измерений.

№п/п	R0,Ом	R1, Ом	R2, Ом	R3, Ом	Uвых, В			,В	,В2
					1	2	3
1	+	-	-	+	1,77	1,74	1,74	1,76	10-4
2	+	-	+	-	0,66	0,66	0,66	0,66	0
3	+	+	-	-	2,1	2,13	2,1	2,11	10-4
4	+	+	+	+	1,59	1,59	1,59	1,59	0
5	+	-	-	-	1,14	1,14	1,17	1,15	10-4
6	+	-	+	+	1,05	1,02	1,02	1,03	10-4
7	+	+	-	+	2,85	2,82	2,85	2,84	10-4
8	+	+	+	-	1,05	1,08	1,05	1,06	10-4

Усреднение значений результатов наблюдений:

;

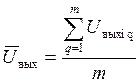где  - результат i наблюдения;

q - номер опыта;

m - количество опыто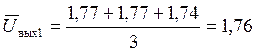в.

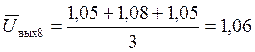 В

…

 В

3 Проверка однородности дисперсий и получение математической модели

Дисперсия среднего значения в каждой строчке таблицы 3, количественно характеризует ошибку воспроизводимости опытов

;

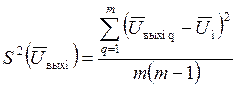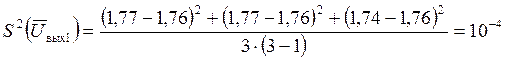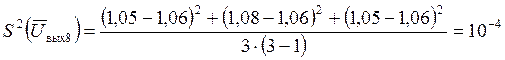 В²

…

 В²

Проверка однородности дисперсий проводиться по критерию Кохрена.

Для трехфакторного эксперимента уравнение регрессии имеет вид:

U_вых = b₀ + b₁R₁ + b₂R₂ + b₃R₃ + b₁₂R₁R₂ + b₁₃R₁R₃ +b₂₃R₂R₃, где х₁, х₂ и х₃ определяют знак коэффициента регрессии в соответствии с планом эксперимента.

Коэффициент регрессии определяется по формуле:

;

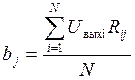где R_ij определяет знак  в соответствии с планом эксперимента, т.е:

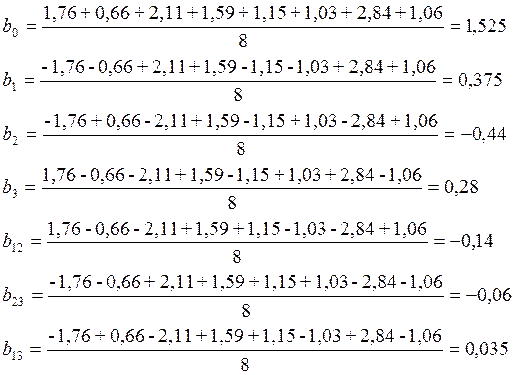
Значимость коэффициентов регрессии оценивается по критерию Стьюдента t следующим образом:

- определяем ошибку эксперимента

;

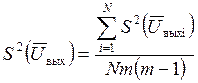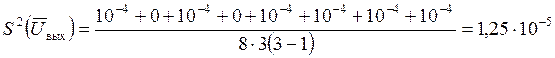 В²;

- дисперсия коэффициента регрессии определяется по формуле

;

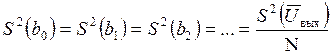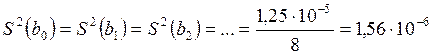 В²;

- коэффициент регрессии значим, если

;

где t выбирается по таблице П3. для трехфакторного эксперимента N = 8 и t = 2,37.

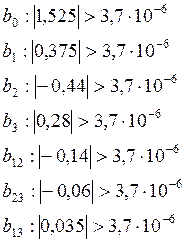
Из расчетов видно, что все коэффициенты регрессии являются значимыми

Подставляя коэффициенты регрессии в уравнение, определяем расчетные значения результатов каждого опыта.

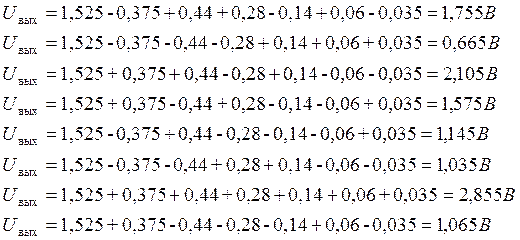
Таблица 4. Сравнения экспериментальных и расчетных значений.

№ п/п	Значения
	Экспериментальные	Расчетные
1	1,76	1,755
2	0,66	0,665
3	2,11	2,105
4	1,59	1,575
5	1,15	1,145
6	1,03	1,035
7	2,84	2,855
8	1,06	1,065

4 Проверка адекватности

Проверка проводиться с помощью критерия Фишера. Критерием адекватности является выполнение условия:

где F_р – расчетное значение критерия Фишера:

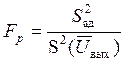
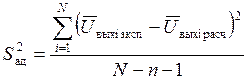
где n – число независимых параметров;

 - значение выходного параметра в эксперименте;

 - расчетное значение выходного параметра.

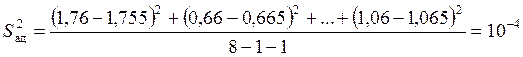В

Значение F_кр находиться по таблице. Для трехфакторного эксперимента при m = 3 F_кр = 3,0.

Критерий адекватности выполняется. Значит, гипотеза адекватности принимается и не нужно переходить к более сложным уравнениям связи, а также для проведения экспериментов не требуется уменьшать интервал варьирования.

Вывод: В ходе лабораторной работы определены значения сопротивлений резисторов при различных условиях эксперимента с учетом матрицы планирования