Математика \ Математические основы проектирования ЭС

Конструирование, разработка технологии и обеспечения надежности РЭА, страница 2

И для данной схемы получилось, что

Находим среднюю наработку на отказ:

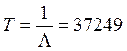(ч).

Вероятность безотказной работы определяется по формуле:

Для различных значений t построена графическая зависимость :

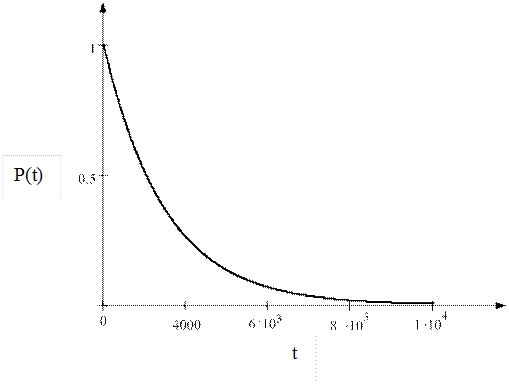
Рисунок 3 - График зависимости вероятности безотказной работы теморона от времени.

Для данного теморона была рассчитана вероятность безотказной работы, и построено графическое отображение зависимости вероятности от времени. Анализ полученного графика показал, что вероятность безотказной работы очень велика на небольшом промежутке времени, что объясняется новизной изделия, далее с увеличением времени возрастает вероятность отказа схемы. Средняя наработка на отказ для данного изделия составляет 37249 часов.

3 Оптимизация параметров

Найти оптимальные параметры и экстремум целевой функции методом линейного программирования.

Предприятие должно выпускать два вида продукции, используя последовательно четыре различных группы производственного оборудования. Выпуск одного комплекта продукции вида А обеспечивает прибыль - 2 млн. руб., продукции вида В - 3 млн. руб. Месячный фонд времени, в днях, каждой группы оборудования и трудоемкость, также в днях, для изготовления комплектов продукции А и В представлены в таблице.

Разработать план производства, который обеспечивает наибольшую прибыль для предприятия.

                                                                                        Таблица 1. 

Группа оборудования

Норма времени на 1 комплект продукции

Фонд времени

a

B

I

3+0,1n

3+0,1n

15+0,1n

II

2+0,1n

6-0,1n

18

III

4-0,1n

0+0,1n

16

IV

1+0,1n

2+0,1n

8+0,1n

n – номер варианта (в данном случае n = 5).

Обозначим за x1 - количество комплектов продукции вида А, а за x2 - количество комплектов продукции вида В. Эти переменные являются положительными независимыми параметрами, для определения которых необходимо составить целевую функцию f(x1, x2) и функции связи (функции ограничения):

 П = f(x1, x2) = 2 × x1+3 × x2 ;       

Получили систему из четырёх уравнений и по паре решений для каждого.       

1) 3,5× x1 + 3,5× x2 £ 15,5;x1 = 0;  x2 = 4,42;

x1 = 4,42; x2 = 0; 

2) 2,5× x1 + 5,5× x2 £ 18;x1 = 0;  x2 = 3,27;

x1 = 7,2; x2 = 0; 

3) 3,5× x1 + 0,5× x2 £ 16;                              x1 = 0;  x2 = 32;

x1 = 4,52; x2 = 0; 

4) 1,5× x1 + 2,5× x2 £ 8,5; x1 = 0;  x2 = 3,4;

x1 = 5,66; x2 = 0; 

Количество комплектов продукции не может быть нецелым числом, поэтому значения x1 и x2  следует округлить до ближайшего целого, а также проверить удовлетворяют ли эти значения условиям 1, 2, 3 и 4.

1) x1 = 0;  x2 = 4;

x1 = 4; x2 = 0;                                           3,5× x1 + 3,5× x2 £ 15,5; 

2) x1 = 0;  x2 = 3;

x1 = 7; x2 = 0;                                           2,5× x1 + 5,5× x2 £ 18; 

3) x1 = 0;  x2 = 32;

x1 = 4; x2 = 0;                                          3,5× x1 + 0,5× x2 £ 16;      

4) x1 = 0;  x2 = 3;

x1 = 5; x2 = 0;                                           1,5× x1 + 2,5× x2 £ 8,5;

Значения x1 и x2  удовлетворяют условиям. Поэтому необходимо найти xi при заданных ограничениях, которые определяют экстремум целевой функции.  Для этого построен график зависимости x2(x1), отражающий область возможных значений (Рис.4 и рис. 5).

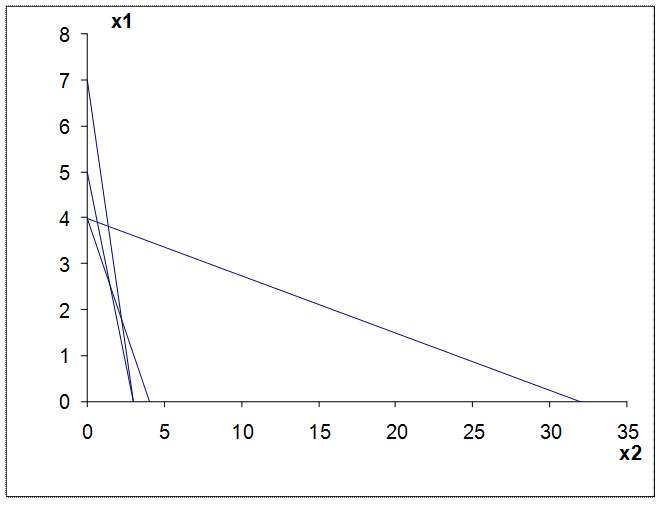
Рис. 4. Зависимости x2(x1)

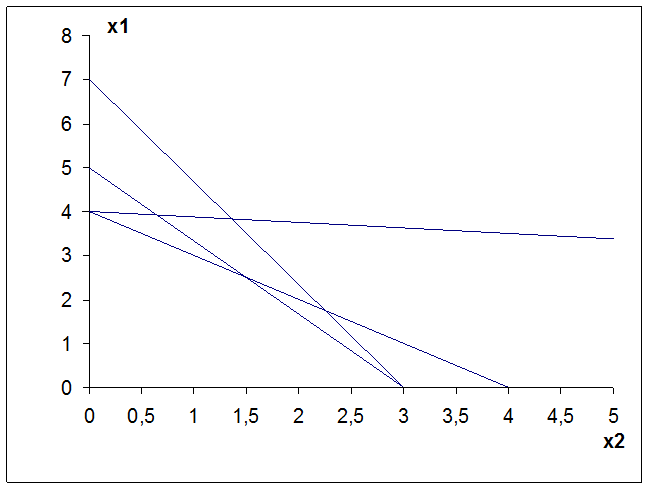
Рис. 5. Зависимости x2(x1) (увеличенный масштаб)

В итоге получили область ограничений: точка 1- x1 = 4;  x2 = 0; точка 2-  x1 = 0;  x2 = 3; точка 3- пересечение прямых x1 = -x2 +4 и x1 = -x2 +5; точка 4-   x1 = 0;  x2 = 0, которая не представляет интереса.

 

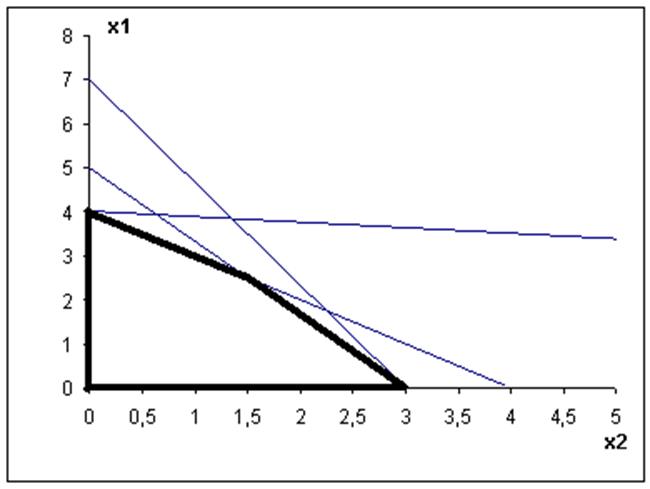
Рис. 6. Область ограничений

Найдена точка 3 пересечений прямых x1 = -x2 +4 и x1 = -x2 +5: x1 = 2,5;  x2 = 1,5.

1(0; 4): ПА = 2·0 + 3·4 = 12 млн. руб

2(3; 0): ПВ = 2·3 + 3·0 = 6 млн. руб

3(2.5; 1.5): ПС = 2·2.5 + 3·1.5 = 9.5 млн. руб

Видно, что максимальная прибыль будет в точке 1 при х1 =0 и х2 = 4 и составляет 12 млн. руб.

Выполняем проверку:

Пусть х1 = 0, х2 = 4, тогда

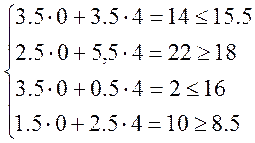
Выполняется только два ограничения, поэтому значение параметра х2 нужно округлять до меньшего целого.

Пусть х1 = 0, х2 = 3, тогда

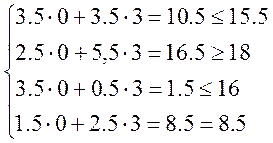
Условия всех ограничений выполняются.

Целевая функция при этом принимает значение

млн. руб

В соответствии с расчетами, план производства, который обеспечит предприятию наибольшую прибыль – продукцию вида А стоит выпускать в двух комплектах, и продукцию вида В выпускать в двух комплектах. При этом прибыль предприятия составит 9 млн. руб.

Список использованной литературы

1.  Талицкий Е. Н. “Теоретические основы конструирования, технологии и надежности РЭА”. Методические указания к курсовой работе. Владимир 1987.

2.  Курс лекции по дисциплине «Математические основы проектирования электронных средств» Е.Н. Талицкого.Владимир,2007.

3.  Журнал «Радио-7», стр.42, 2005.

Скачать файл