Проверка гипотезы о нормальном законе распределения статистических данных. Измеренные значения параметров элементов, страница 2

В качестве однотипных радиоэлементов использовались резисторы с номинальным сопротивлением 1 кОм, в качестве измерительного прибора – мультиметр. При этом:

R_min=930 Ом;

R_max=1080 Ом;

∆=(1080-930)/10=15.

3. Результаты расчётов

Результаты обработки экспериментальных данных приведены в таблице 1.

Таблица 1

Интервал	Середина интервала	Частота	Относит. Частота	Накопл. Частота	Относит. накопл. частота
930-944	937	3	0.027	3	0.027
945-959	952	0	0	3	0.027
960-974	967	13	0.117	16	0.144
975-989	982	37	0.333	53	0.477
990-1004	997	45	0.4	98	0.877
1005-1019	1012	8	0.072	106	0.949
1020-1034	1027	3	0.027	109	0.976
1035-1049	1042	1	0.009	110	0.985
1050-1064	1057	0	0	110	0.985
1065-1080	1072	1	0.009	111	0.994

Относительная частота определяется:

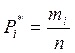, где m_i – абсолютная частота попадания параметра x в интервал;

n – общее число статистических данных (n=111).

Высота прямоугольника гистограммы находится по формуле:

.

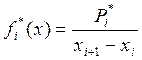Для каждого столбца она будет равна:

Высота прямоугольника кумулятивной кривой равна:

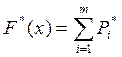
На основе данных таблицы 1 и расчётов высота прямоугольника гистограммы строятся гистограмма, накопленный полигон и кумулятивная кривая.

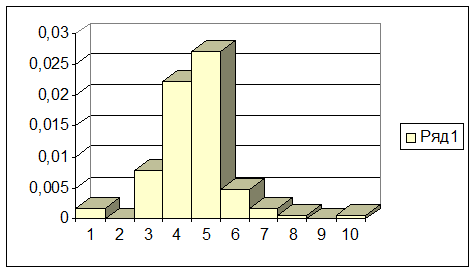
Рисунок 1

Гистограмма

2

1

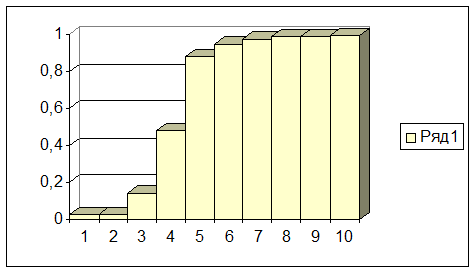
Рисунок 2

Накопленный полигон (1) и кумулятивная прямая (2)

Среднее арифметическое значение сопротивления резистора:

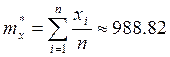
Приближённое значение среднего арифметического:

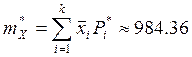
Наиболее точно параметр расчитывается по первой формуле, следовательно в дальнейшем

Расчёт ведётся по первому значению.

Приближённое значение статистической дисперсии:

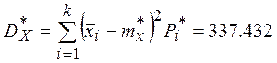
Среднеквадратическое отклонение:

Медиана: 995 Ом

Мода: 975 Ом

4. Проверка гипотезы о нормальном законе распределения. Метод моментов

Теоритическая кривая плотности нормального распределения расчитывается по формуле:

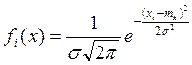
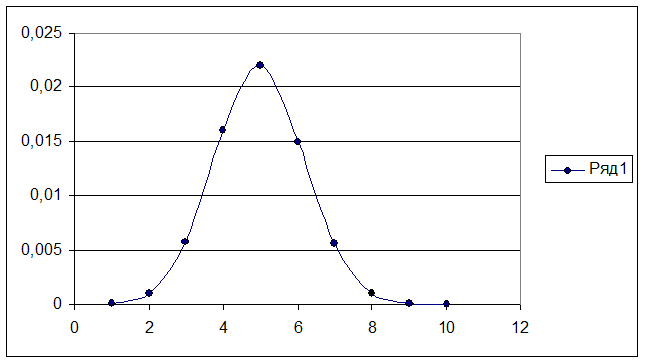
Рисунок 3

Теоритическая кривая плотности нормального распределения

При нормальном законе распределения теоретическая вероятность P_i определяется:

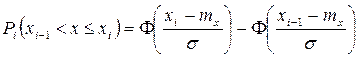
Интервал	Относительная частота	Вероятность
930-944	0.027	0,005642	0,081
945-959	0	0,039	0,039
960-974	0.117	0,142	0,004357
975-989	0.333	0,273	0,013
990-1004	0.4	0,277	0,06
1005-1019	0.072	0,148	0,039
1020-1034	0.027	0,042	0,005291
1035-1049	0.009	0,006241	0,001227
1050-1064	0	0,000488	0,000488
1065-1080	0.009	0,00002011	4,017

Критерий пирсона равен:

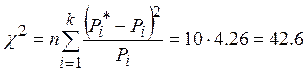
5. Проверка гипотезы о нормальном законе распределения. Метод вероятностных сеток

Рисунок 4

График функции распределения F(x)

График функции нормального распределения в общем случае представляет кривую. Соответствующим преобразованием F(x) и x удаётся сделать график прямолинейным.

, , где L – принятая нами ширина графика, мм; .

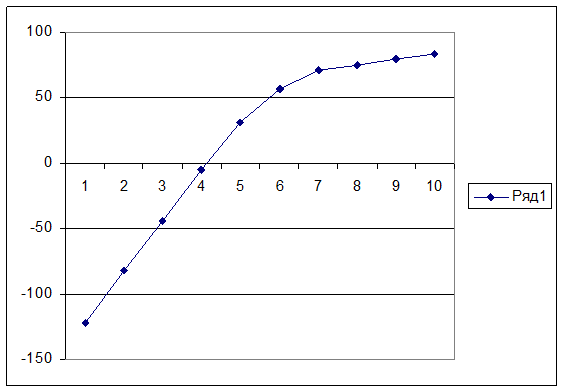
Рисунок 5

График функции нормального распределения на вероятностной бумаге

6. Вывод: в ходе выполнения данной лабораторной работы была проведена проверка гипотезы о нормальном законе распределения статистических данных (в роли которых выступали резисторы номинальным сопротивлением 1 кОм). Была произведена проверка гипотезы о нормальном законе распределения методом моментов и методом вероятностных сеток. При проверке гипотезы о нормальном законе распределения методом моментов критерий Пирсона оказался равным 42.6 а соответствующая ему вероятность – 0.9999>0.8, значит гипотеза принимается, но в методе вероятностных сеток точки не лежат на одной прямой, но отклоняются от её положения только в интервалах с меньшей вероятностью, следовательно гипотеза верна.