































соответствии с полученными данными
производится расчет профилей большого и малого зеркала, соответственно
параболоида и гиперболоида вращения. Используя программу "Antenn2"
получаем в соответствии с формулами, описывающими законы плоскостей для
параболоида 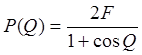 , [
1 ] для
гиперболоида
, [
1 ] для
гиперболоида 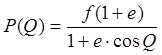 [ 1 ]
[ 1 ]
Профиль большого зеркала в координатной системе с началом в вершине параболы (x0, y0) определяется уравнением:
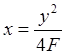 [
[
[ 2 ] Профиль малого зеркала может быть построен в координатной системе с помощью соотношения:
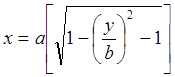 [ 2 ]
[ 2 ]
![]()
![]() , где
, где ![]() и
и ![]() являются полуосями
гиперболы.
являются полуосями
гиперболы.
Профиль параболоида вращения:
Для значений F= 0.13705 M, Do= 0.46 M
|
Q° |
P(0) |
X,m |
Y,m |
Q° |
P(0) |
X,m |
Y,m |
|
1 |
0.13706 |
0.13704 |
0.13704 |
42 |
0.15724 |
0.11686 |
0.10522 |
|
2 |
0.13709 |
0.13701 |
0.00478 |
43 |
0.15832 |
0.11578 |
0.10797 |
|
3 |
0.13714 |
0.13696 |
0.00718 |
44 |
0.15942 |
0.11468 |
0.11074 |
|
4 |
0.13722 |
0.13688 |
0.00957 |
45 |
0.16056 |
0.11354 |
0.11354 |
|
5 |
0.13731 |
0.13679 |
0.01197 |
46 |
0.16174 |
0.11236 |
0.11635 |
|
6 |
0.13743 |
0.13667 |
0.01436 |
47 |
0.16296 |
0.11114 |
0.11918 |
|
7 |
0.13756 |
0.13654 |
0.01676 |
48 |
0.16422 |
0.10988 |
0.12204 |
|
8 |
0.13772 |
0.13638 |
0.01917 |
49 |
0.16551 |
0.10859 |
0.12491 |
|
9 |
0.13790 |
0.13620 |
0.02157 |
50 |
0.16685 |
0.10725 |
0.12781 |
|
10 |
0.13810 |
0.13600 |
0.02398 |
51 |
0.16823 |
0.10587 |
0.13074 |
|
11 |
0.13832 |
0.13578 |
0.02639 |
52 |
0.16965 |
0.10445 |
0.13369 |
|
12 |
0.13856 |
0.13554 |
0.02881 |
53 |
0.17112 |
0.10298 |
0.13666 |
|
13 |
0.13883 |
0.13527 |
0.03123 |
54 |
0.17263 |
0.10147 |
0.13966 |
|
14 |
0.13912 |
0.13498 |
0.03366 |
55 |
0.17419 |
0.09991 |
0.14269 |
|
15 |
0.13943 |
0.13467 |
0.03609 |
56 |
0.17580 |
0.09830 |
0.14574 |
|
16 |
0.13976 |
0.13434 |
0.03825 |
57 |
0.17745 |
0.09665 |
0.14882 |
|
17 |
0.14011 |
0.13399 |
0.04096 |
58 |
0.17916 |
0.09494 |
0.15194 |
|
18 |
0.14049 |
0.13361 |
0.04341 |
59 |
0.18092 |
0.09318 |
0.15508 |
|
19 |
0.14089 |
0.13321 |
0.04587 |
60 |
0.18273 |
0.09137 |
0.15825 |
|
20 |
0.14131 |
0.13279 |
0.04833 |
61 |
0.18460 |
0.08950 |
0.16146 |
|
21 |
0.14176 |
0.13234 |
0.0508 |
62 |
0.18653 |
0.08757 |
0.1647 |
|
22 |
0.14223 |
0.13187 |
0.05328 |
63 |
0.18852 |
0.08558 |
0.16797 |
|
Q° |
P(0) |
X,m |
Y,m |
Q° |
P(0) |
X,m |
Y,m |
|
23 |
0.14272 |
0.13138 |
0.05577 |
64 |
0.19056 |
0.08354 |
0.17128 |
|
24 |
0.14324 |
0.13086 |
0.05826 |
65 |
0.19267 |
0.08143 |
0.17462 |
|
25 |
0.14379 |
0.13031 |
0.06077 |
66 |
0.19485 |
0.07925 |
0.178 |
|
26 |
0.14435 |
0.12975 |
0.06328 |
67 |
0.19709 |
0.07701 |
0.18142 |
|
27 |
0.14495 |
0.12915 |
0.06581 |
68 |
0.1994 |
0.0747 |
0.18488 |
|
28 |
0.14557 |
0.12853 |
0.06834 |
69 |
0.20179 |
0.07231 |
0.18838 |
|
29 |
0.14622 |
0.12788 |
0.07089 |
70 |
0.20424 |
0.06986 |
0.19193 |
|
30 |
0.14689 |
0.12721 |
0.07344 |
71 |
0.20678 |
0.06732 |
0.19551 |
|
31 |
0.14759 |
0.12651 |
0.07601 |
72 |
0.20939 |
0.06471 |
0.19915 |
|
32 |
0.14832 |
0.12578 |
0.07860 |
73 |
0.21209 |
0.06201 |
0.20282 |
|
33 |
0.14908 |
0.12502 |
0.08119 |
74 |
0.21487 |
0.05923 |
0.20655 |
|
34 |
0.14986 |
0.12424 |
0.0838 |
75 |
0.21774 |
0.05636 |
0.21032 |
|
Q° |
P(0) |
X,m |
Y,m |
Q° |
P(0) |
X,m |
Y,m |
|
35 |
0.15067 |
0.12343 |
0.08642 |
76 |
0.22071 |
0.05339 |
0.21415 |
|
36 |
0.15152 |
0.12258 |
0.08906 |
77 |
0.22376 |
0.05034 |
0.21803 |
|
37 |
0.15239 |
0.12171 |
0.09171 |
78 |
0.22692 |
0.04718 |
0.22196 |
|
38 |
0.15330 |
0.12080 |
0.09438 |
79 |
0.23018 |
0.04392 |
0.22595 |
|
39 |
0.15424 |
0.11986 |
0.09706 |
80 |
0.23355 |
0.04055 |
0.23 |
|
40 |
0.15521 |
0.11889 |
0.09976 |
81 |
0.23702 |
0.03708 |
0.2341 |
|
41 |
0.15621 |
0.11789 |
0.10248 |
||||
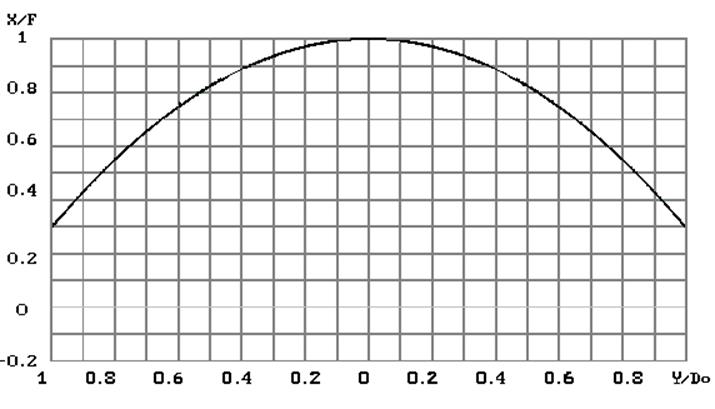
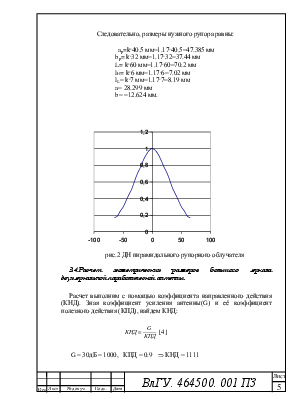
рис. 4 Профиль параболоида вращения при фокусе F = 0.13705м
Профиль гиперболоида вращения (для значений f = 0.00707 M, e = 5.41148 , do = 0.0460 M)
|
Q° |
P(0) |
X,m |
Y,m |
Q° |
P(0) |
X,m |
Y,m |
|
1 |
0.00707 |
0.00707 |
0.00012 |
41 |
0.00892 |
0.00673 |
0.00585 |
|
2 |
0.00707 |
0.00707 |
0.00025 |
42 |
0.00903 |
0.00671 |
0.00604 |
|
3 |
0.00708 |
0.00707 |
0.00037 |
43 |
0.00914 |
0.00669 |
0.00624 |
|
4 |
0.00708 |
0.00707 |
0.00049 |
44 |
0.00926 |
0.00666 |
0.00644 |
|
5 |
0.00709 |
0.00707 |
0.00062 |
45 |
0.00939 |
0.00664 |
0.00664 |
|
6 |
0.00710 |
0.00706 |
0.00074 |
46 |
0.00952 |
0.00662 |
0.00685 |
|
7 |
0.00711 |
0.00706 |
0.00087 |
47 |
0.00966 |
0.00659 |
0.00707 |
|
8 |
0.00713 |
0.00706 |
0.00099 |
48 |
0.00981 |
0.00656 |
0.00729 |
|
9 |
0.00714 |
0.00706 |
0.00112 |
49 |
0.00996 |
0.00654 |
0.00752 |
|
10 |
0.00716 |
0.00705 |
0.00124 |
50 |
0.01012 |
0.00651 |
0.00775 |
|
11 |
0.00718 |
0.00705 |
0.00137 |
51 |
0.01029 |
0.00648 |
0.00800 |
|
Q° |
P(0) |
X,m |
Y,m |
Q° |
P(0) |
X,m |
Y,m |
|
12 |
0.00720 |
0.00705 |
0.00150 |
52 |
0.01046 |
0.00644 |
0.00825 |
|
13 |
0.00723 |
0.00704 |
0.00163 |
53 |
0.01065 |
0.00641 |
0.00850 |
|
14 |
0.00725 |
0.00704 |
0.00175 |
54 |
0.01084 |
0.00637 |
0.00877 |
|
15 |
0.00728 |
0.00703 |
0.00188 |
55 |
0.01105 |
0.00634 |
0.00905 |
|
16 |
0.00731 |
0.00703 |
0.00201 |
56 |
0.01126 |
0.00630 |
0.00933 |
|
17 |
0.00734 |
0.00702 |
0.00215 |
57 |
0.01148 |
0.00625 |
0.00963 |
|
18 |
0.00737 |
0.00701 |
0.00228 |
58 |
0.01172 |
0.00621 |
0.00994 |
|
19 |
0.00741 |
0.00701 |
0.00241 |
59 |
0.01197 |
0.00616 |
0.01026 |
|
20 |
0.00745 |
0.00700 |
0.00255 |
60 |
0.01223 |
0.00612 |
0.01059 |
|
21 |
0.00749 |
0.00699 |
0.00268 |
61 |
0.01251 |
0.00606 |
0.01094 |
|
22 |
0.00753 |
0.00698 |
0.00282 |
62 |
0.01280 |
0.00601 |
0.01130 |
|
23 |
0.00758 |
0.00698 |
0.00296 |
63 |
0.01311 |
0.00595 |
0.01168 |
|
24 |
0.00763 |
0.00697 |
0.00310 |
64 |
0.01344 |
0.00589 |
0.01208 |
|
25 |
0.00768 |
0.00696 |
0.00324 |
65 |
0.01379 |
0.00583 |
0.01250 |
|
26 |
0.00773 |
0.00695 |
0.00339 |
66 |
0.01416 |
0.00576 |
0.01294 |
|
27 |
0.00779 |
0.00694 |
0.00353 |
67 |
0.01455 |
0.00569 |
0.01340 |
|
28 |
0.00785 |
0.00693 |
0.00368 |
68 |
0.01497 |
0.00561 |
0.01388 |
|
29 |
0.00791 |
0.00692 |
0.00383 |
69 |
0.01542 |
0.00553 |
0.01440 |
|
30 |
0.00797 |
0.00690 |
0.00399 |
70 |
0.01590 |
0.00544 |
0.01494 |
|
31 |
0.00804 |
0.00689 |
0.00414 |
71 |
0.01641 |
0.00534 |
0.01552 |
|
32 |
0.00811 |
0.00688 |
0.00430 |
72 |
0.01696 |
0.00524 |
0.01613 |
|
33 |
0.00818 |
0.00686 |
0.00446 |
73 |
0.01755 |
0.00513 |
0.01679 |
|
34 |
0.00826 |
0.00685 |
0.00462 |
74 |
0.01819 |
0.00501 |
0.01749 |
|
35 |
0.00834 |
0.00683 |
0.00479 |
75 |
0.01888 |
0.00489 |
0.01824 |
|
36 |
0.00843 |
0.00682 |
0.00495 |
76 |
0.01963 |
0.00475 |
0.01905 |
|
Q° |
P(0) |
X,m |
Y,m |
Q° |
P(0) |
X,m |
Y,m |
|
37 |
0.00852 |
0.00680 |
0.00513 |
77 |
0.02044 |
0.00460 |
0.01992 |
|
38 |
0.00861 |
0.00679 |
0.00530 |
78 |
0.02133 |
0.00443 |
0.02086 |
|
39 |
0.00871 |
0.00677 |
0.00548 |
79 |
0.02230 |
0.00426 |
0.02189 |
|
40 |
0.00881 |
0.00675 |
0.00566 |
80 |
0.02337 |
0.00406 |
0.02301 |
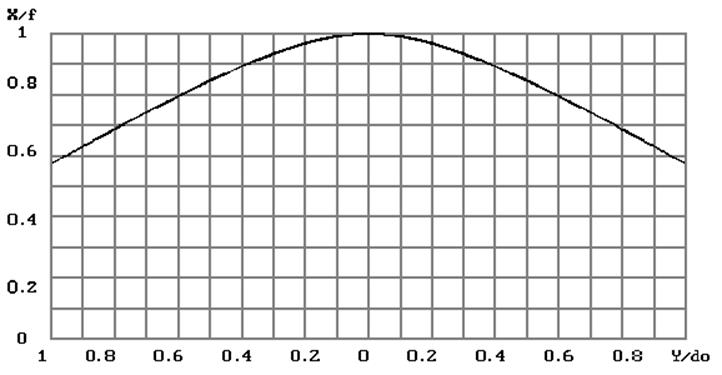
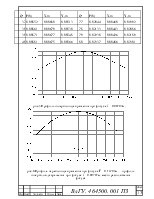
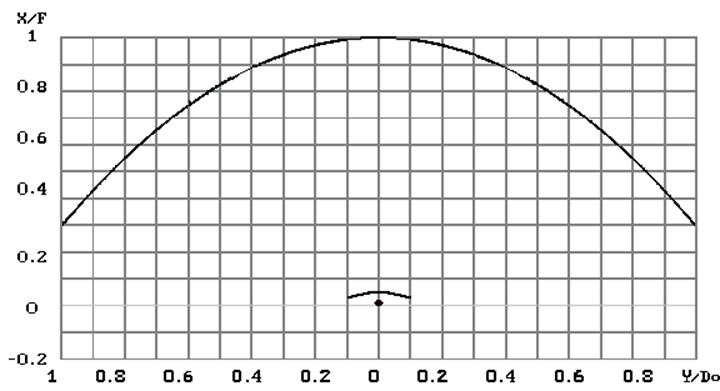 рис.5 Профиль гиперболоида вращения при фокусе f =
0.00707м,
рис.5 Профиль гиперболоида вращения при фокусе f =
0.00707м,
рис.6 Профиль параболоида вращения при фокусе F = 0.13705м , профиль гиперболоида вращения при фокусе f = 0.00707м, место расположения фокуса
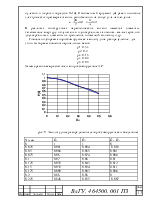
3.6. Расчет амплитудного распределения в раскрыве большого зеркала без учета затенения.
В качестве исходных данных взяты следующие переменные:
Do, do - диаметры большого и малого зеркал соответственно;Ψ0 - угол раствора образующей параболы;
φ2 - угол облучения источником краев малого зеркала;
Fo(Q) - нормированная диаграмма направленности облучателя;
Эксцентриситет, фокусные расстояния малого и большого зеркал рассчитываются по формулам, приведенным в n.3.
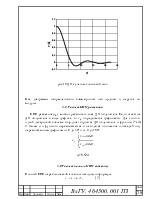
Амплитудное распределение на апертуре большого зеркала:
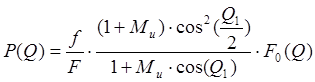 [
1 ]
[
1 ]
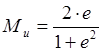 [ 1 ]
[ 1 ]
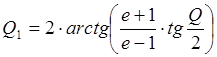 [ 1 ]
[ 1 ]
Перевод P0(Q) в P0(X) осуществляется путем пересчета:
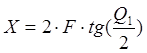 [ 1 ]
[ 1 ]
Расчет амплитудного распределения в плоскости основного зеркала
Данные к расчету:
1. Диаметр большого зеркала [ Do, м ] = 0.46
2. Диаметр малого зеркала [ do, м ] = 0.046
3. Угол раствора образующей параболы [Ψ0,°] = 80
4. Угол облучения малого зеркала [ φ2, °] = 60
5. Эксцентриситет гиперболы [ e ] = 5.41148
6. Фокусное расстояние гиперболы [ f, м ] = 0.00707
7. Фокусное расстояние параболы [ F, м ] = 0.13705
Результаты расчета:
|
Q° |
P(Q) |
X,m |
Xнорм. |
P(X) |
|
0 |
1 |
0 |
0 |
1 |
|
5 |
0.98013 |
0.01739 |
0.07562 |
0.98013 |
|
10 |
0.92591 |
0.03485 |
0.15153 |
0.92591 |
|
15 |
0.85419 |
0.05245 |
0.22803 |
0.85419 |
|
20 |
0.75648 |
0.07024 |
0.30541 |
0.75648 |
|
25 |
0.67674 |
0.08832 |
0.38399 |
0.67674 |
|
30 |
0.57847 |
0.10674 |
0.46410 |
0.57847 |
|
35 |
0.47298 |
0.12561 |
0.54611 |
0.47298 |
|
40 |
0.39736 |
0.14500 |
0.63041 |
0.39736 |
|
45 |
0.32008 |
0.16501 |
0.71744 |
0.32008 |
|
50 |
0.24642 |
0.18576 |
0.80767 |
0.24642 |
|
55 |
0.19670 |
0.20738 |
0.90165 |
0.19670 |
|
60 |
0.14250 |
0.23000 |
1 |
0.14250 |

рис.7 Амплитудное распределение
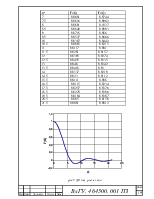
3.7. Расчет диаграммы направленности без учета и с учетом затенения
Определение ДН параболических антенн связано с вычислением интеграла по криволинейной поверхности зеркала, возбуждаемой электрическими токами(токовый метод) или интеграла по плоской поверхности выходного зеркала – апертуре (апертурный метод).
Апертурный метод значительно проще в реализации и часто обеспечивает точность достаточную в инженерных расчетах. Его простота обусловлена тем, что эквивалентный электрический и магнитный токи в апертуре являются синфазными и под интегралом остается только функция АР.
Для апертур прямоугольной и круглой форм имеются такие АР, для которых интегрирование приводит к известным функциям и вычисление ДН сильно упрощается.
Эти АР называются парциальными(ПАР). Им соответствуют парциальные ДН.
Мы вычисляем ДН в соответствии с теоремой о ДН антенны с составным АР: Если
нормированное АР(g) представляется в виде линейной комбинации
нормированных парциальных АР(gi) со своими весами (pi),
то ДН(F(θ)) является линейной комбинацией соответствующих
нормированных ПАР(F(θ))с теми же весами, умноженными на параметры
парциальных АР(Мi). Если 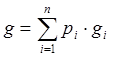 , то
, то 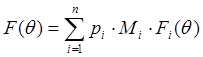
Нормированное амплитудное распределение (АР) в раскрыве может быть представлено в виде суммы пяти парциальных:
1 – равномерного с весом р1,
2 – квадратичной параболы с весом р2,
3 – квадратичной параболы в квадрате с весом р3,
4 – квадратичной параболы в кубе с весом р4,
5 – линейно убывающего до нуля на краю с весом р5.
Первое распределение дает подставку – пьедестал АР, остальные спадающие к краю до нуля дают возможность подбором весов (pj) аппроксимировать имеющиеся в антенне АР или подобрать АР, удовлетворяющее требованиям.
Увеличение скорости спадания АР к краю раскрыва приводит к расширению главного максимума ДН, характеризуемого коэффициентом расширения луча (КРЛ), снижению коэффициента использования поверхности (КИП) и уровня боковых лепестков (УБЛ).
Формулы ДН пяти ПАР, используемых для аппроксимации АР.
|
№ ПАР |
Нормированная парциальная ДН |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
Нормированные парциальные ДН выражаются через функции Бесселя первого рода разных порядков Jn(u) и комбинацию функций Бесселя и Струве нулевого и первого порядков Нn(u). Обобщенный аргумент (u) равен половине электрического размера антенны, умноженного на синус угла наблюдения.
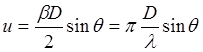
В реальных конструкциях параболических антенн имеются элементы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.