1. Цель работы:
Изучение метода матричных испытаний и экспериментальное определение работоспособности усилителя низкой частоты (УНЧ).
2. Блок-схема измерений, краткое описание лабораторного макета.
Блок-схема измерений:
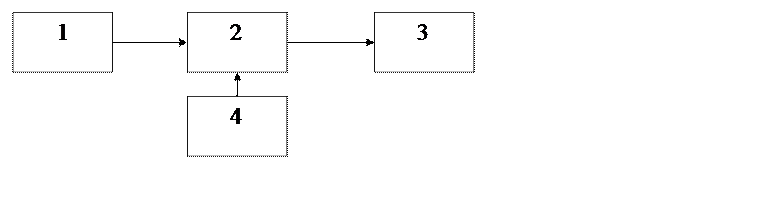
1- генератор;
2- УНЧ;
3- милливольтметр;
4- источник питания.
Устройство смонтировано в виде макета, установленного в термошкафу. При заданном напряжении на входе при помощи галетных переключателей устанавливаются различные значения параметров двух резисторов и измеряются выходные напряжения.
3. Матрица ситуаций и результаты испытаний.
|
αi |
R1 |
R2 |
U2 при U1=9,5 |
K1i |
U2 при U1=10 |
K2i |
U2 при U1=10,5 |
K3i |
|||
|
1 |
125 |
2,4 |
69 |
7,26 |
+ |
66,3 |
6,63 |
- |
69 |
6,57 |
- |
|
2 |
125 |
2,1 |
72 |
7,58 |
+ |
69 |
6,90 |
+ |
71,7 |
6,83 |
+ |
|
3 |
125 |
1,9 |
68 |
7,16 |
+ |
70,5 |
7,05 |
+ |
71,1 |
6,77 |
- |
|
4 |
125 |
1,6 |
64,5 |
6,79 |
- |
63 |
6,30 |
- |
63 |
6,00 |
- |
|
5 |
110 |
2,4 |
72 |
7,58 |
+ |
72,6 |
7,26 |
+ |
72,6 |
6,91 |
+ |
|
6 |
110 |
2,1 |
72,6 |
7,64 |
+ |
72,3 |
7,23 |
+ |
72 |
6,86 |
+ |
|
7 |
110 |
1,9 |
72,6 |
7,64 |
+ |
72 |
7,20 |
+ |
72,6 |
6,91 |
+ |
|
8 |
110 |
1,6 |
66 |
6,95 |
+ |
66,3 |
6,63 |
- |
66,3 |
6,31 |
- |
|
9 |
95 |
2,4 |
74,4 |
7,83 |
- |
74,4 |
7,44 |
+ |
80,7 |
7,69 |
+ |
|
10 |
95 |
2,1 |
78 |
8,21 |
- |
78,3 |
7,83 |
- |
78,9 |
7,51 |
+ |
|
11 |
95 |
1,9 |
76 |
8,00 |
- |
78,4 |
7,84 |
- |
78,6 |
7,49 |
+ |
|
12 |
95 |
1,6 |
66 |
6,95 |
+ |
72,6 |
7,26 |
+ |
69,9 |
6,66 |
- |
|
13 |
80 |
2,4 |
79,5 |
8,37 |
- |
83,4 |
8,34 |
- |
78,6 |
7,49 |
+ |
|
14 |
80 |
2,1 |
83,7 |
8,81 |
- |
84 |
8,40 |
- |
81 |
7,71 |
+ |
|
15 |
80 |
1,9 |
83,7 |
8,81 |
- |
83,7 |
8,37 |
- |
81,6 |
7,77 |
+ |
|
16 |
80 |
1,6 |
78 |
8,21 |
- |
78,3 |
7,83 |
- |
75,3 |
7,17 |
+ |
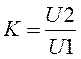
Если коэффициент усиления K уходит за пределы поля допуска, то это считается отказом УНЧ. Возьмём поле допуска:
![]() .
.
Тогда « - » соответствует отказу, а « + » - работоспособной ситуации.
Рассчитаем вероятность того, что схема окажется работоспособной.
4. Расчёт вероятности работоспособного состояния УНЧ.
Вероятность того, что схема окажется работоспособной, выразится так:
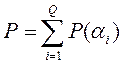 , где Q – число работоспособных ситуаций, Q = 26; Р(αi)
– вероятность i-ой работоспособной ситуации. Число
возможных ситуаций N = 48.
, где Q – число работоспособных ситуаций, Q = 26; Р(αi)
– вероятность i-ой работоспособной ситуации. Число
возможных ситуаций N = 48.
Вероятность Р(αi) находят как произведение вероятностей нахождения параметров в соответствующих квантах. При нормальном законе распределения эти вероятности могут быть найдены по формуле:
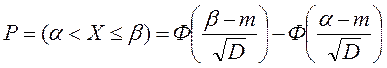 , где Ф(z) – функция Лапласа; α, β – границы кванта; m, D – математическое ожидание и дисперсия.
, где Ф(z) – функция Лапласа; α, β – границы кванта; m, D – математическое ожидание и дисперсия.
Найдём вероятности нахождения параметра R1 в его квантах.
|
R1 |
125 |
110 |
95 |
80 |
|
Квант |
(132,5;117,5) |
(117,5;102,5) |
(102,5;87,5) |
(87,5;72,5) |
|
z1 |
0,77 |
0,00 |
-0,77 |
-1,55 |
|
Ф(z1) |
0,78 |
0,00 |
-0,78 |
-0,94 |
|
z2 |
1,55 |
0,77 |
0,00 |
-0,77 |
|
Ф(z2) |
0,94 |
0,78 |
0,00 |
-0,78 |
|
P |
0,16 |
0,78 |
0,78 |
0,16 |
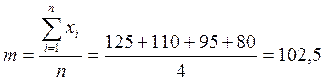
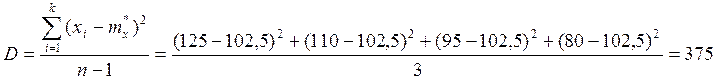
![]()
Найдём вероятности нахождения параметра R2 в его квантах.
|
R2 |
2,4 |
2,1 |
1,9 |
1,6 |
|
Квант |
(2,6;2,3) |
(2,3;2) |
(2;1,7) |
(1,7;1,4) |
|
z1 |
0,88 |
0,00 |
-0,88 |
-1,76 |
|
Ф(z1) |
0,83 |
0,00 |
-0,83 |
-0,96 |
|
z2 |
1,76 |
0,88 |
0,00 |
-0,88 |
|
Ф(z2) |
0,96 |
0,83 |
0,00 |
-0,83 |
|
P |
0,13 |
0,83 |
0,83 |
0,13 |
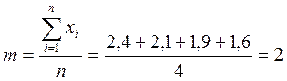
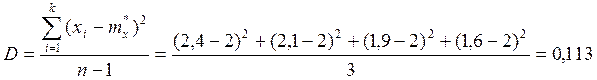
![]()
Вероятность работоспособности схемы:
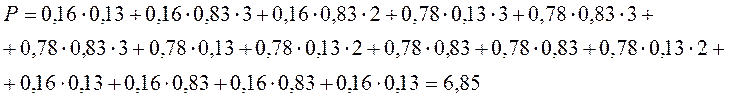
Эту же вероятность можно найти как:
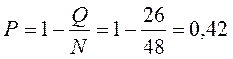
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.