Прямоугольный резонатор. Исследование электромагнитного поля в прямоугольном резонаторе, страница 3

При построении структуры поля нужно учесть, что в объемном резонаторе, созданном на базе прямоугольного волновода, характер изменения поля вдоль поперечных координат Х и У такой же, как и в волноводе. Необходимость соблюдения граничных условий у поперечных стенок резонатора ()  приводит к тому, что электрическое и магнитное поля в объемном резонаторе смещаются относительно друг друга на четверть длины волны по сравнению с положением полей в волноводе. Таким образом, структуру поля в объемном резонаторе можно построить по известной картине поля в волноводе с теми же индексами m и n ( см. например [8.1, с. 222-223] ).

7.3. Для построения структуры распределения токов на стенках волновода (п.3.2 домашнего задания) необходимо знать вектор поверхностной плотности тока проводимости . Величину и направление   определяют из граничных условий для тангенциальных составляющих магнитного поля у идеального металла

,                                             (7.2)

где     - вектор магнитного поля у стенки резонатора;

 - нормаль к поверхности, направленная из металла.

7.4. Способы возбуждения колебаний в резонаторах (п.3.3 домашнего задания) совпадают c соответствующими способами возбуждения волн заданного типа в волноводах (см. [8.1, с. 279-281] ).

Общие принципы возбуждения волноводов изложены также в указаниях к лабораторной работе №4 настоящего пособия.

7.5. При определении длины объемного резонатора для получения резонанса на колебаниях заданного типа (п.3.4 домашнего задания) следует иметь в виду, что резонансная частота  связана с геометрическими параметрами резонатора а, b, l и параметрами среды , заполняющей резонатор, соотношением

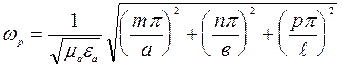.                   (7.3)

Используя (7.3), нетрудно получить выражение для резонансной длины прямоугольного резонатора l: 

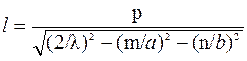    ,                         ( 7.4 )

где 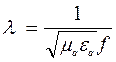  - резонансная длина волны.

7.6. Расчет добротности ненагруженного прямоугольного резонатора (п.3.5 домашнего задания) с колебаниями магнитного и электрического типов может быть выполнен с помощью соотношений , приведенных в [8.1, с. 363-370]. Например, для колебаний типа  в прямоугольном резонаторе добротность определяется соотношением

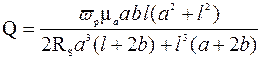,                              (7.5)

где 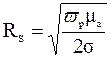 - активная часть поверхностного сопротивления металлических стенок резонатора.

Выражение (7.5) справедливо для ненагруженного объемного резонатора. Это необходимо принять во внимание при сравнении результатов расчета и эксперимента.

Реально достижимые цифры добротностей, как правило, несколько ниже предсказываемых теоретическими формулами (в том числе и (7.5)), поскольку они не учитывают потери в трущихся контактах между боковой поверхностью и подвижным короткозамыкателем, с помощью которого настраивается  резонатор. Кроме того, расчетные соотношения не учитывают шунтирующего действия внешних цепей, оказывающих влияние через элементы связи.

7.7. При исследовании характера изменения добротности прямоугольного объемного резонатора в зависимости от частоты колебаний и объема (при изменении длины) следует иметь в виду интегральное соотношение для добротности объемного резонатора (см. [8.1, с. 239-241]).

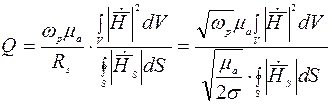
          8. Библиография.

Федоров Н.Н. Основы электродинамики: Учеб. пособие для вузов. - М.: Высш. шк., 1980. - С.224-229, 238-241, 375-378.