Геометрическая оптика. Вычисление поля в излучающей апертуре

соответствии с принципом эквивалентности эту апертуру надо окружить замкнутой поверхностью. Обычно эту поверхность располагают так, чтобы она совпадала с излучающей апертурой и неизлучающей поверхность антенны. Т.к. предполагается, что эти антенны изготовлены из идеального металла, то на неизлучающей поверхности , а поверхностный магнитный ток , то  поле считается заданным только в излучаемой апертуре

При расчетах антенн пренебрегают затеканием поверхностного электрического тока на не излучаемую поверхность антенны , т. е. .

Таким образом, на замкнутой поверхности, обтягивающей антенну, тангенциальные компоненты поля равны нулю везде, кроме S_S (излучаемой поверхности).

Далее задачу решают следующим образом. Используя принцип эквивалентности в излучающем разрыве, переходят от известного распределения электромагнитного поля к известному распределению фиктивных источников.

Обычно в дальнейшем при вычислении поля используют принцип суперпозиции, т. е. излучающий раскрыв разбивают на элементарные площадки (затем, чтобы в пределах каждой площадки распределение токов и фаз можно было считать постоянным).

Затем вычисляют поле в точке наблюдения как сумму полей, создаваемых отдельными элементарными площадками. Эти поверхностные элементарные излучатели называются элементами Гюйгенса.

10.5 Элемент Гюйгенса

В качестве элемента Гюйгенса можно рассматривать элементарный фрагмент фазового фронта распространяющейся волны.

Используя принцип эквивалентности, перейдем к поверхностным токам:

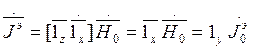
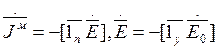
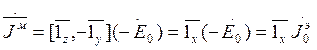
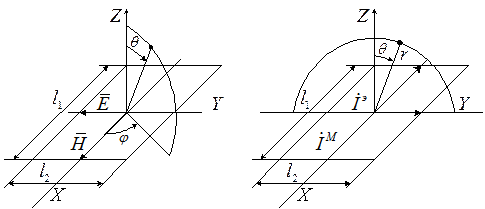
Учитывая, что размеры площадки маленькие, можно считать, что амплитуды этих токов постоянны. Введем сферическую систему координат с центром в середине площадки, в пределах этой площадки протекают токи. Эти токи будут ортогональны друг другу, их амплитуда считается неизменной.

Таким образом, задача нахождения поля, возбуждаемого элементом Гюйгенса, эквивалентна задаче нахождения поля, возбуждаемого находящимися в одной плоскости и ортогональными друг другу электрическим и магнитным излучателями.

Вычислим поле, возбуждаемое подобной системой в плоскости ZOY (плоскость вектора Е). При этом

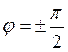
Соотношения для поля в ДЗ ЭЭИ:

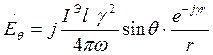
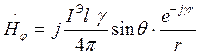
Преобразуем:

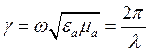
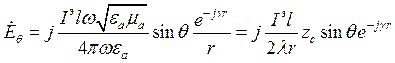
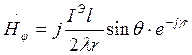
Соотношение для ЭМИ:

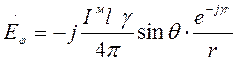
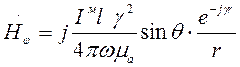
Преобразуем:

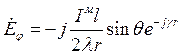
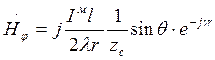
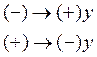
Расчет проведем для электрического вектора. Определим результирующее поле, возбуждаемое ЭЭИ, длина которого , в плоскости ZOY:

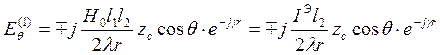                т.к.               

Определим поле, возбуждаемое ЭМИ, электрического вектора в плоскости ZOY.

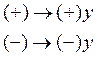
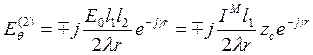   т.к.

Плоскость ZOY перпендикулярна ЭМИ, т. е. она находится в максимуме излучения ЭМИ, т. е. в соотношении q примем равным 90⁰ (т. е. sinq=1). Найдем результирующее поле:

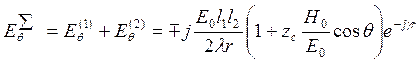
Аналогичным образом получим выражения для поля в плоскости ЭМИ (XOZ). Для плоскости угла j:

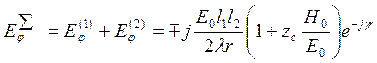
“ – ” относится к Х>0, “+” относится к X<0.

Получим выражение для результирующих электрических полей в двух ортогональных плоскостях в ДЗ. При произвольных q и j результирующее поле выглядит так (S-поверхность фазового фронта):

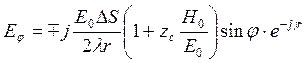
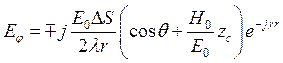
Если отношение 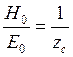 справедливо, тогда и упрощаются:

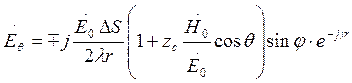
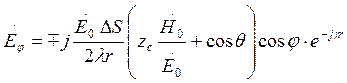
Абсолютная величина электрического вектора в дальней зоне произвольной плоскости, проходящей через ось Z:

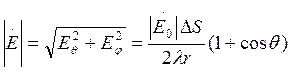
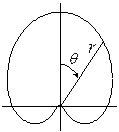Распределение поля  не зависит от угла j, так как поле по углу j  является асимметричным.

Кроме того, из видно, что элемент Гюйгенса обладает направленными свойствами.

Из следует, что нормированная диаграмма направленности будет выглядеть следующим образом в полярной системе координат