Полукубические множества и свободные частично коммутативные моноиды, страница 2

Теорема 1. Пусть FPCM - категория свободных частично-комутативных моноидов и плоских гомоморфизмов. Тогда для любой малой категории J и функтора  существует копредел ^JD.

Доказательство. Пусть D(i)=M(E_i.I_i) для всех iÎJ. Для любого морфизма  ÎMorJ  гомоморфизм D(α): D(i)®D(j) является плоским ,откуда D(α)(Е_i) ÍE{1}. В категории моноидов существуют копределы. Если они заданы с помощью образующих и соотношений, то копредел можно задать с помощью дизъюнктного объединения множеств образующих с  соотношениями для моноидов и с соотношениями  х=у , в случае D(α)(х)=у.

Отсюда копределом будет моноид  порожденный множеством и соотношениями

1.  ab=ba   ;

2.  а_i=b_j , в случае .

Если удалить отождествляемые элементы из и элементы равные 1, получим множество Е, порождающее моноид, и соотношения вида ab=ba, где аb,  а1 и

b1. Эти пары (a,b) отнесем к множеству I. Получим копредел ^JD.

Пример 4. Пусть Е₁={a}, I₁ = Æ ,  E₂ ={a,b} , I₂ = { (a,b),(b,a)},  Е₃={a,c}, I₃ = Æ . Вычислим копредел диаграммы

М(E₃, I₃) ¬  M(Е₁, I₁ ) ®М(E₂, I₂)  ,

заданной с помощью гомоморфизмов

M(Е₁, I₁ ) ®М(E₂, I₂) , {a}    {a,b},     

M(Е₁, I₁ ) ®М(E₃, I₃) , {a}    {a,b,с},

Копредел будет определяться с помощью кодекартового квадрата

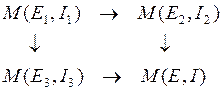
Получаем Е={a,b,c}, I={(a,b),(b,a)}. В этом случае моноид порожден тремя элементами, два из которых перестановочны.

§3. Категория полукубических множеств.

          Определение 3 . Полукубическим множеством Х=(Х,) называется последова-тельность множеств ( Х) и семейство отображений : Х ®Х определенных при 1≤ i ≤ n, eÎ{0,1}, и удовлетворяющих условию коммутативности диаграмм для всех a, bÎ{0,1}, n³2, 1≤ i < j ≤ n :

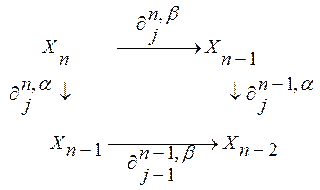
          Полукубические множества как функторы. Пусть  ₊  -    категория, состоящая из конечных частично упорядоченных множеств I={0,1}, равных декартовой степени линейно упорядоченного множества  I={0,1}. Морфизмы этой категории определяются как возрастающие отображения частично упорядоченных множеств, допускающих разложение в композицию отображений вида ,где

(х₁,…..,х_к-1 )=( х₁,…,х_i-1,e,x_i,…, х_к-1  ), eÎI, 1≤ i ≤ k.

Благодаря соотношениям  при 1≤ i < j ≤ n, Î {0,1} , bÎ{0,1}, каждый морфизм этой категории  допускает каноническое разложение  , 1≤ j₁ <…..< j_n-m ≤ n . Это позволяет определить полукубическое множество как функтор  Х: ®Set,  принимающий значения Х(I)=Х_n   на объектах и Х(f)=  - на морфизмах . Определяя морфизмы как естественные преобразования , приходим  к категории полукубических множеств Set

Лемма 1. Пусть FPCM - категория свободных частично-комутативных моноидов и плоских гомоморфизмов. Существует функтор FPCMSet.

Доказательство.  Т(М(Е,I))={(e,….,e): eeи (e, e)I1<j}

  

Теорема 2. Существует пара сопряженных функторов FPCM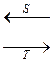Set

Доказательство. Построим функтор H: ₊®FPCM. Положим H(Iⁿ)=Nⁿ. Значения  Н на морфизмах будут определены отображениями H():N^n-1®Nⁿ  на морфизмах          I^n-1Iⁿ _,  действующими по формуле H()(x₁,…,x_n-1)=( x₁,…,x _i-1,0,x_i,…x_n-1).

Из леммы 3 следует существование сопряженных функторов.

Описание функторов S и T. Согласно общей теории Т(М(Е,I)) будет функтором ®Set, определенным как Т(М(Е,I))(-)= FPCM(Н(-),М(Е,I)). Отсюда вытекает, что значения на объектах будут равны Т(М(Е,I))_n = FPCM(Nⁿ, М(Е,I)). Но,  поскольку морфизмы в FPCM являются плоскими гомоморфизмами , то

Т(М(Е,I))_n={( x₁,…,x_n ):( x_iÎEÈ{1} для всех 1£I£n) & (x_ix_j=x_jx_i  для всех (x_i,x_j)ÎI)}, и ( x₁,…,x_n)= ( x₁,..x_i-1,x_i+1,…,x_n). Функтор S: Set®FPCM строится следующим образом. Рассмотрим комма-категорию h_*/X  для произвольного объекта ХÎSet. Её объекты – естественные преобразования  hX. Морфизмами служат коммутативные диаграммы

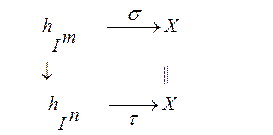
Существует забывающий функтор Q_X: h_*/X® ₊ и определена композиция функторов

h_*/X  ₊FPCM. Согласно общей теории S(X)=  ^h*/X (H)

Действие S на f: X®Yопределено коммутативной диаграммой

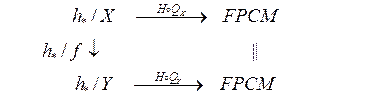
Определяющее для каждого морфизма полукубических множеств f отображение

 ^h*/X(H)® ^h*/Y (H)

§4. Заключение.

Элементам свободных частично коммутативных моноидов соответствуют вычислительные процессы. Полукубическим множествам соответствуют автоматы высших размерностей. Мы доказали, что каждой вычислительной системе можно сопоставить автомат высшей размерности. И наоборот, каждому автомату можно сопоставить вычислительную систему, которая является универсальной и строится естественным образом.