Группы гомологий асинхронных систем переходов. Практическое решение задач, страница 3

Доказательство. Рассмотрим более общую ситуацию, когда функтор  определен для некоторых малой категории  и принимает значения в категории , обладающей копределами. Согласно [2], функтор  допускает продолжение до некоторого функтора , сопряженного слева к функтору  ставящего в соответствие объектам функторы  и очевидным образом продолжающегося на морфизмы  категории . Легко видеть, что имеет место изоморфизм категорий  где  - вложение Ионеды. Этот изоморфизм устанавливается сопоставлением естественному преобразованию  морфизма . Обозначим через  функтор, сопоставляющий каждому объекту  категории объект , морфизму между  и , заданному с помощью  сопоставляется . Для любого функтора , отождествляя категории  и , получаем, что левое расширение Кана функтора  вдоль функтора  (в терминологии и обозначениях [4]) изоморфно, согласно [5, Лемма 1.1], функтору, принимающему значения 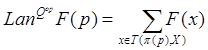. Левые производные  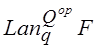равны нулю при . Отсюда получаем с помощью спектральной последовательности Андре из [2, Приложения 2] изоморфизмы  при . Подставим теперь . В силу утверждения [5, Лемма 1.1.] о действии морфизмов правого расширения Кана получим, что  на объектах принимает значения , а на морфизмах  определяется гомоморфизмами .

Замечание. Поскольку произведение неединичных элементов моноида  не равно единице, то аналогично [5, Приложение 2.2.] получаем, что  изоморфны группам гомологий комплекса  в котором морфизмы  не равны тождественным.

Для любых двух малых категорий ,  и функторов  рассмотрим функтор  определенный по формуле .

Лемма 2.3. Для любых малых категорий  и , коммутативного кольца с единицей и функторов  модули гомологий  изоморфны модулям гомологий тензорного произведения комплексов  и .

Доказательство. Рассмотрим тензорное произведение симплициальных модулей . Согласно теореме Эйленберга - Зильбера [6, гл. VIII, Теорема 8.1.] комплекс, соответствующий тензорному произведению симплициальных модулей  гомотопически эквивалентен тензорному произведению комплексов . Имеет место изоморфизм симплициальных модулей  

Пусть  произвольная малая категория. Полная подкатегория  называется открытой, если для любых  она содержит все объекты ,для которых существуют морфизмы . В случае категории  вместе с каждым состоянием  она должна содержать все состояние , достижимые из .

Для любого функтора  определенного на открытой подкатегории  существует продолжение , полученное добавлением нулей  и . Полученный функтор является левым расширением Кана, функтора  вдоль вложения [2].

Имеют место изоморфизмы для всех , в силу изоморфизмов комплексов.

Определение. Модулями гомологий  для открытой подкатегории  называются модули , где - функтор, равный коядру естественного преобразования . Здесь  обозначает функтор, принимающий постоянные значения, равные на объектах из  и равные  - на морфизмах.

Очевидно, что  при  и  при . Следующее утверждение показывает, что для модулей гомологий на классе пар асинхронных систем переходов имеет место аксиома точности. Оно вытекает непосредственно из длинной точной последовательности, соответствующей короткой точной последовательности в категории функторов.

Предложение 2.4. Пусть открытые подкатегории, соответствующие пространству состояний . Тогда существует точная последовательность

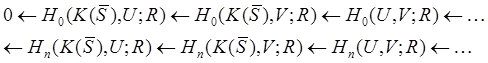
Для асинхронной системы переходов  определим локальные модули гомологий по формуле , где  наименьшая открытая подкатегория в , содержащая начальное состояние . Ясно, что . Рассмотрим случай . Положим .

Теорема 2.5. Пусть  и  -асинхронные системы переходов. Тогда имеют место изоморфизмы абелевых групп , для всех  .

Доказательство. По лемме 2.3 группы  изоморфны группам гомологий тензорного произведения комплексов, соответствующих симплициальным абелевым группам  и . Поскольку эти комплексы состоят из свободных абелевых групп, и группы циклов и границ не имеют кручения, то, согласно [6, гл.V, теорема 10.2], имеет место точная последовательность, расщепляющиеся на каждом месте,  приводящая к искомой формуле.

Списоклитературы.

[1] Nielsen M., Winskel G. Petri Nets and Bisimulations. Aarhus,  1995. 36 p. (Preprint / Aarhus Univ; BRICS Report Series RS – 95 – 4.)

[2] Габриель П., Цисман М. Категории частных и теория гомотопий. М.: Мир, 1971.

[3] Husainov A.A., Calisici H. Flows in Graphs and Homology of Free Categories. Preprint, 2001. 11 p. http://arxiv.org/abs/math.CT/0106146.

[4] MacLane S. Categories for the Working Mathematician. Berlin: Springer-Verlag, 1971.

[5] Хусаинов А.А. Сравнение размерностей малой категории // Сиб. мат. журн. 1997. Т.38, №6. С. 1413-1426.

[6] Маклейн С. Гомология. М.: Мир, 1966.