































Перестановки из n элементов, образующие верхнюю и нижнюю строки подстановки F, имеют либо одинаковые четности (т. е. они обе четны, или обе нечетны), либо противоположные четности (т. е. одна четная, а другая нечетная), причем совпадение или несовпадение четностей перестановок не зависит от различных способов записи данной подстановки
Умножение подстановок. По определению подстановка n-й степени есть взаимно однозначное отображение Fконечного множества из n различных элементов на себя. Последовательное выполнение двух подстановок n-й степени опять будет взаимно однозначным отображением множества А на себя и приводит к некоторой вполне определенной третьей подстановке n-й степени, называемой произведением первой из заданных подстановок на вторую.
О произведении двух подстановок Fи G также говорят, что оно получено в результате умножения подстановки Fна подстановку G. Произведение подстановки Fна подстановку G обозначают FG.
3.3. Размещения.
Пусть дано некоторое конечное множество А, состоящее из п различных элементов. Выберем некоторым образом из п элементов т различных элементов и будем составлять из этих т элементов различные упорядоченные множества.
Конечные упорядоченные
подмножества, содержащие по т элементов, выбранных из п элементов
основного множества, называются размещениями из п элементов по т
элементов. Число всех возможных размещений из п элементов по от
обозначается ![]() .
.
Нетрудно убедиться, что
![]()
т е. один элемент из п можно
выбрать п способами, а из одного элемента можно образовать единственное
упорядоченное множество. Найдем, чему равно число размещений из n элементов по т. Чтобы
распределить т+1 элементов, взятых из п элементов , по m+1 местам, можно сначала
выбрать т элементов и разместить их по первым т местам. Это можно
сделать ![]() способами. При каждом
таком выборе т элементов из п остаются «свободными» п — т элементов,
любой из которых можно поставить на свободное (m+1)-е место. Таким образом,
при каждом из
способами. При каждом
таком выборе т элементов из п остаются «свободными» п — т элементов,
любой из которых можно поставить на свободное (m+1)-е место. Таким образом,
при каждом из ![]() заполнений первыхт
мест получим (п - m) возможных заполнений (m+ 1)-го места. Следовательно, число размещений по m+ 1 элементов, выбранных из п
заданных элементов, связано с числом размещений из п элементов по m равенством
заполнений первыхт
мест получим (п - m) возможных заполнений (m+ 1)-го места. Следовательно, число размещений по m+ 1 элементов, выбранных из п
заданных элементов, связано с числом размещений из п элементов по m равенством
![]()
Учитывая, что ![]() , имеем
, имеем
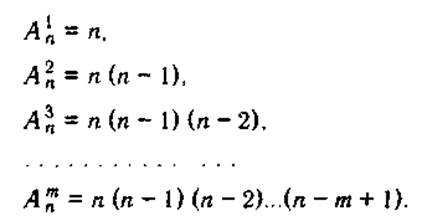
Последнее равенство можно записать с использованием символа факториала
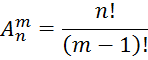
При т = 0 получаем ![]() , т. е. из любого
множества единственным способом можно извлечь пустое множество, которое, по определению,
можно упорядочить единственным способом.
, т. е. из любого
множества единственным способом можно извлечь пустое множество, которое, по определению,
можно упорядочить единственным способом.
Число размещений и число перестановок связаны формулой
![]()
3.4. Сочетания.
Конечные неупорядоченные множества, содержащие т различных
элементов, выбранных из п элементов заданного множества, называются сочетаниями
из п элементов по т. Число сочетаний из п элементов
по т элементов обозначается ![]() .
.
Найдем, чему равно
число сочетаний из п элементов по m. В согласии с данным выше
определением размещений, из данного множества, содержащего п элементов,
можно образовать ![]() различных
упорядоченных множеств, содержащих по т различных элементов. Из
множества, содержащего т различных элементов, можно образовать
различных
упорядоченных множеств, содержащих по т различных элементов. Из
множества, содержащего т различных элементов, можно образовать ![]() различных упорядоченных множеств, а потому число
различных упорядоченных множеств, а потому число ![]() различных
неупорядоченных множеств, содержащих по т различных элементов, выбранных
из элементов, будет вычисляться по формуле
различных
неупорядоченных множеств, содержащих по т различных элементов, выбранных
из элементов, будет вычисляться по формуле
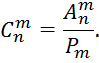
Используя формулы для
подсчета числа перестановок ![]() и числа размещений
и числа размещений ![]() , получим
, получим
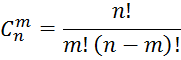
Для числа сочетаний справедливы равенства
![]() (2)
(2)
а также
![]() .
.
Последнее свойство иногда формулируется в виде следующей теоремы о конечных множествах.
Число всех подмножеств
множества, состоящего из п элементов, равно ![]() .
.
3.6. Перестановки с повторениями.
Пусть А —
некоторая совокупность, состоящая из п элементов т различных
типов (т ![]() п)
п)
![]()
причем элементы одного типа неразличимы между
собой. И пусть ![]() элементов принадлежат первому типу,
элементов принадлежат первому типу, ![]() — второму,
— второму, ![]() — третьему,
— третьему, ![]() — m-му типу, причем
— m-му типу, причем ![]() . Например, если
. Например, если
![]() (3)
(3)
то, считая элементами первого типа
единицы, элементами второго типа двойки, а элементами третьего типа тройки,
имеем ![]() .
.
Различные конечные
совокупности, содержащие п элементов, из которых ![]() принадлежат первому типу,
принадлежат первому типу, ![]() — второму, ...,
— второму, ..., ![]() — m-му типу, называются перестановками
с повторениями (кортежами
— m-му типу, называются перестановками
с повторениями (кортежами
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.