

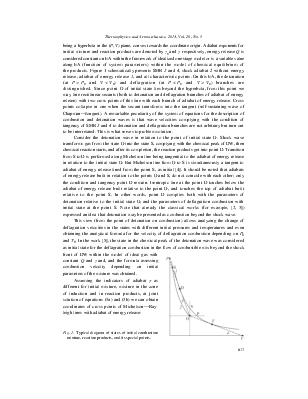




combustion expressed through Mach number of the shock wave and the compression degree behind it:
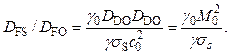 (8)
(8)
Reducing the known relation for pressure behind the SW front as a function of Mach number of SW Р = f(M)
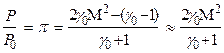 (9)
(9)
to the form M = g(P), rewrite the relation between the deflagration velocities, from which the linear dependence of combustion velocity on the temperature of initial state of combustible mix is apparent [5]:
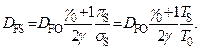 (10)
(10)
The latter formula, in addition, is the substantiation of a rather arbitrary formula (1).
To verify the latter relation we calculated the parameters of combustion and detonation of stoichiometric mixtures of hydrogen and typical hydrocarbons (methane, ethylene, and acetylene, as representatives with single, double, and triple chemical bonds) with oxygen and air at varying initial pressure in the range 0.001-100 atm and initial temperature in the range 200-1800 K, knowingly exceeding the areas of application [6]. Some results are presented in Figs. 2-5.
In addition, we calculated the parameters of combustion and detonation at initial state complying with the point S (simultaneous change of Р and Т). It should be emphasized that the condition Q = const along the adiabat of energy release is a strong idealization, justified only by the possibility of simple algebraic transformation of the laws of conservation. Already in approximation of chemical equilibrium of the products, Q changes along the adiabat: for example, for the mixture 2Н2 + О2 at specific points of adiabats QD = 972.6, QV = 1057.5, QP = 1117.6, and QDF = 1199.7 cal/g. If we select the state at the point S as initial, then at point D, being the deflagration point, QDF = 1580.4 cal/g. Comparing with the value Q for the point D as detonation point relative to the state О (QD = 972.6 cal/g), note that these values considerably differ (see above mentioned on non-coincidence of adiabats of energy release for the points О and S).
|
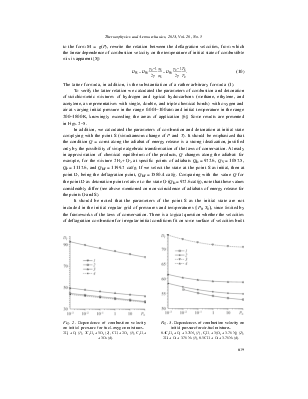
Fig. 2. Dependence of combustion velocity on initial pressure for fuel-oxygen mixtures. 2H2 + O2 (1), 2C2H2 + 5O2 (2), CH4 + 2O2 (3), C2H4+ + 3O2 (4). |
|
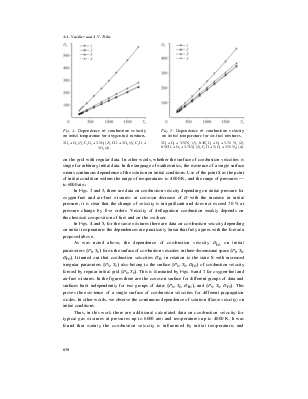
Fig. 3. Dependences of combustion velocity on initial pressure for air-fuel mixtures. 0.4C2H2 + O2 + 3.76N2 (1), C2H4 + 3(O2 + 3.76 N2) (2), 2H2 + O2 + 3.76 N2 (3), 0.5CH4 + O2 + 3.76N2 (4). |
It should be noted that the parameters of the point S as the initial state are not included in the initial regular grid of pressures and temperatures {P0, T0}, since limited by the frameworks of the laws of conservation. There is a logical question whether the velocities of deflagration combustion for irregular initial conditions fit on some surface of velocities built on the grid with regular data. In other words, whether the surface of combustion velocities is single for arbitrary initial data. In the language of mathematics, the existence of a single surface means continuous dependence of the solution on initial conditions. Use of the point S as the point of initial condition widens the range of temperatures to 4000 K, and the range of pressures — to 6000 atm.
|
Fig. 4. Dependence of combustion velocity on initial temperature for oxygen-fuel mixtures. 2H2 + O2 (1), C2H2 + 2.5O2 (2), CH4 + 2O2 (3), C2H4 + 3O2 (4). |
|
Fig. 5. Dependence of combustion velocity on initial temperature for air-fuel mixtures. 2H2 + O2 + 3.76N2 (1), 0.4C2H2 + O2 + 3.76 N2 (2), 0.5CH4 + O2 + 3.76N2 (3), C2H4 + 3(O2 + 3.76 N2) (4). |
In Figs. 2 and 3, there are data on combustion velocity depending on initial pressure for oxygen-fuel and air-fuel mixtures: at common decrease of D with the increase in initial pressure, it is clear that the change of velocity is insignificant and does not exceed 20 % at pressure change by five orders. Velocity of deflagration combustion weakly depends on the chemical composition of fuel and on the oxidizer.
In Figs. 4 and 5, for the same mixtures there are data on combustion velocity depending on initial temperature: the dependences are practically linear that fully agrees with the formula proposed above.
As was noted above, the dependence of combustion velocity
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.