Динамическое программирование. Задачи об инвестировании, замене оборудования, кратчайшего пути через сеть, страница 2

Планируется эксплуатация оборудования в течение некоторого периода времени продолжительностью 5 лет (n=5). Оборудование имеет тенденцию с течением времени стареть и приносить все меньшую годовую прибыль r(t), где t – возраст оборудования. При этом есть возможность в начале любого года продать устаревшее оборудование за цену С(t), которая, разумеется, тоже зависит от возраста, и купить новое оборудование за цену Р. = 26.

Требуется найти оптимальный план замены оборудования при условии, что суммарная прибыль за все 5 лет была максимальной. Годовая прибыль и остаточная стоимость в зависимости от возраста задаются таблицей

t	0	1	2	3	4	5
r(t)	24	22	22	20	16	12
C(t)	22	20	16	14	10	6

Возраст оборудования к началу эксплуатационного периода t₀ = 1 год.

Решение. 1.Разобьем процесс решения задачи замены оборудования на 5 (m=5) шагов, т.е. разобьем весь период эксплуатации на 5 этапов.

2.В начале каждого года можно принять решение: сохранить оборудование С₀ или заменить его новым З₀.

3.После t лет эксплуатации (1≤t≤5) оборудование можно продать за остаточную стоимость С(t).

Первый этап. Условная оптимизация

4.Вычислим максимально возможную прибыль только за последний год.

Шаг k=m=5.

,

,

,

,

.

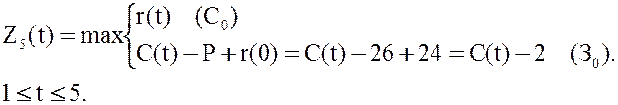
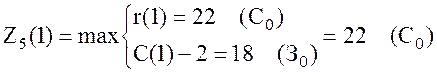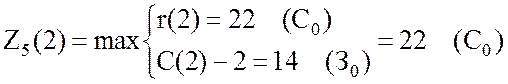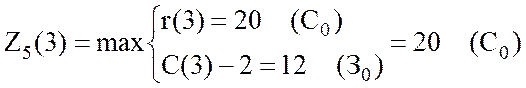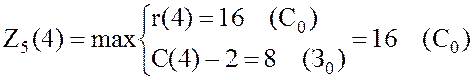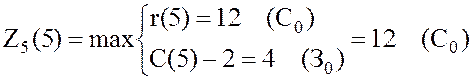Шаг k-1=m-1=4.

,

,

,

.

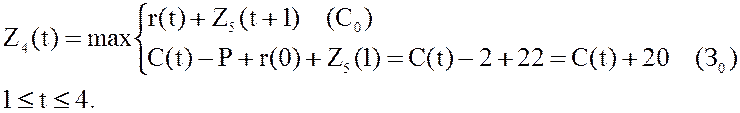
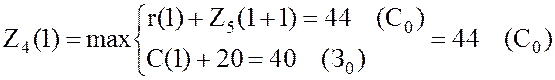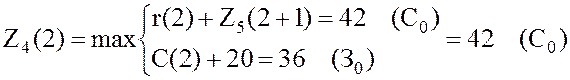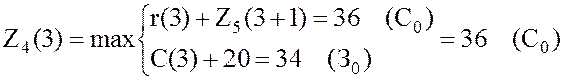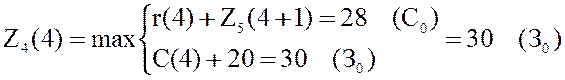Шаг k-2=m-2=3.

,

,

,

.

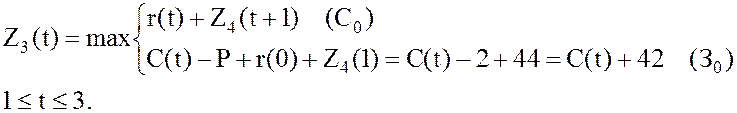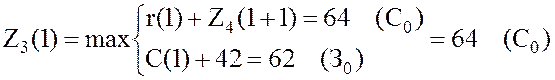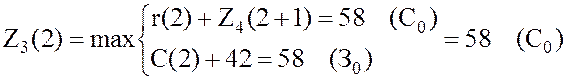Шаг k-3=m-3=2.

,

.

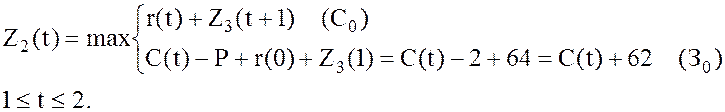
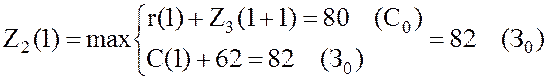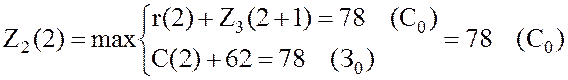Шаг k-4=m-4=1.

.

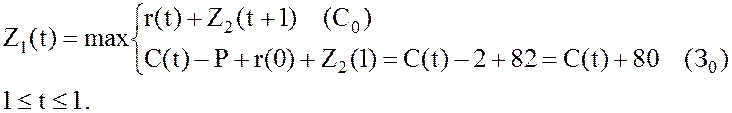
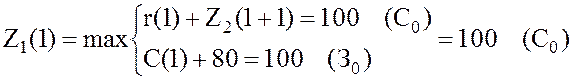Второй этап. Безусловная оптимизация

Начинаем с первого шага

k=1, Z₁ (t=1) = 100             (С₀)

k=2, Z₂ (t=1) = 82                (З₀)

k=3, Z₃ (t=1) = 64               (С₀)

k=4, Z₄ (t=1) = 44               (С₀)

k=5, Z₅ (t=1) = 22               (С₀)

или   Z₅ (t=2) = 22              (С₀)

Очевидно, что максимально возможная прибыль от эксплуатации оборудования за годы  с 1-го по 5-й  Z^* = Z₁(1) = 100 достигается, если на 1-м году не производить замену оборудования, тогда к началу второго года возраст оборудования будет равен двум годам.

При этом для получения максимума прибыли за оставшиеся (со 2-го по 5-й) годы необходимо оборудование заменить.

К началу третьего года возраст оборудования станет равным 1 году.

В этом случае максимум прибыли за годы с 3 - го по 5- й достигается также, если оборудование сохранить.

К началу четвертого года возраст оборудования станет равным 2 году и т.д.

Таким образом, замену оборудования надо производить один раз в начале второго года эксплуатации.

10.3. Задача кратчайшего пути через сеть

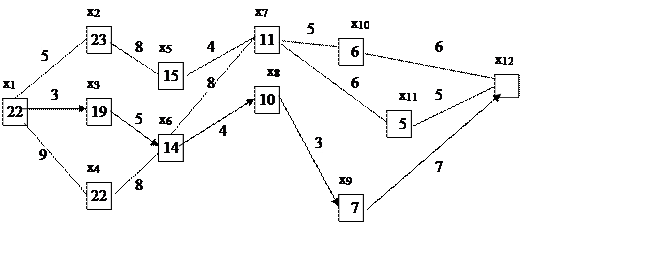
Транспортная сеть состоит из 12 (m=12) узлов (городах), некоторые из которых соединены магистралями. Стоимость проезда по каждой из таких магистралей известна и отмечена на схеме (рис. 1).

Требуется найти оптимальный маршрут из 1-го пункта в 12-й. Движение только слева направо.

Решение

1-Так как движение только слева направо, то попав, например, в 9-й, 10-й и 11-й пункты, мы имеем право переместиться только в 12-й пункт и не можем возвратиться в 7-й или 8-й пункты.

Рис. 1

Это (в совокупности с особенностями данной схемы)  дает нам право отнести каждый из 12 пунктов к одному из пяти поясов.

Будем говорить, что пункт принадлежит k-му поясу, если из него можно попасть в конечный (12-й) пункт ровно за k шагов, т.е. с заездом ровно в k-1 промежуточный пункт. Таким образом, пункты 9, 10 и 11 принадлежат к первому поясу; 7 и 8 – ко второму; 5 и 6 – к третьему; 2, 3 и 4 – к четвертому; 1 – к пятому.

2- Функцией Беллмана на k-м шаге решения задачи Z_k(U) назовем минимально возможную стоимость проезда из города U (k-го пояса) до конечного пункта.

Для первого шага (k=1) – это стоимость проезда из городов 1-го пояса (х₉, х₁₀, х₁₁) непосредственно до конечного пункта   .

.

.

.

.

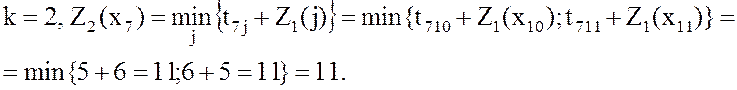
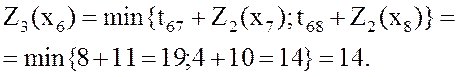
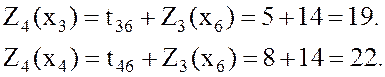
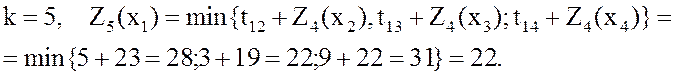3- Минимально возможная стоимость проезда из пункта 1 в пункт 12 ,   Z^* = Z₅(x₁) = 22 и оптимальный маршрут 

х₁®х₃®х₆®х₈®х₉®х₁₂.