Коммутация вентилей в схемах выпрямителей. Среднее значение или постоянная составляющая падения выпрямленного напряжения, обусловленного коммутацией, страница 4

2) Определяется индуктивное сопротивление рассеяния фазы трансформатора

Ом.

3) В соответствии с (1.11) определяется максимальная выпрямленная ЭДС

В.

4) В соответствии с (1.50), с учетом (1.62), определяется ток нагрузки:

.

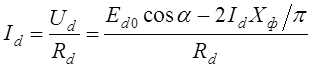После несложных преобразований последнего выражения окончательно определяется ток нагрузки

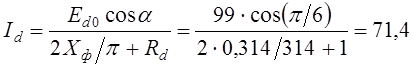А.

5) По (1.59) находится ток двух входящих в работу вентилей, например  и

.

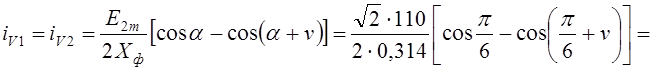
6) В соответствии с (1.60) определяется ток двух вентилей, выходящих из работы

.

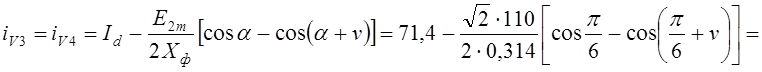
7) По формуле (1.61) определяется угол коммутации

.

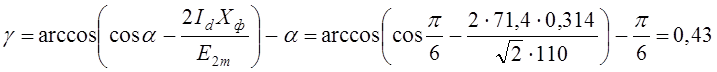8) В соответствии с (1.62) записывается уравнение внешней характеристики

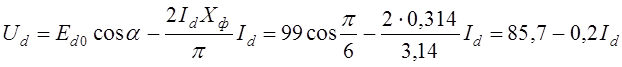, по которому строится характеристика (рис. 1.22).

9) По результатам расчета строится кривые мгновенных значений токов и напряжения. На интервалах коммутации выпрямленное напряжение в однофазных схемах равно нулю. Кривые приводятся на рис 1.23.

Рис. 1.22. Внешняя характеристика однофазной мостовой схемы

1.6.2. Рассчитать и построить кривые мгновенных значений выпрямленного напряжения и тока вентилей  и  в трехфазной мостовой схеме (см. рис. 1.1). Рассчитать и построить внешнюю характеристику этой схемы выпрямления. ЭДС питающей сети =220 В. Коэффициент трансформации силового трансформатора =2, индуктивность рассеяния фазы трансформатора =0,001 Гн и соответственно индуктивное сопротивление рассеяния при частоте сети 50 Гц равно 0,314 Ом. Угол отпирания вентилей 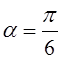. Активное сопротивление цепи нагрузки =1 Ом. Индуктивность в цепи нагрузки достаточно велика, вследствие чего ток нагрузки можно считать идеально гладким.

Рис. 1.23. Токи и напряжения в однофазной мостовой схеме

Порядок расчета следующий:

1) Определяется действующее значение фазной ЭДС

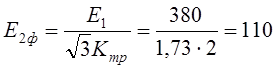В.

2) По выражению (1.35) определяется максимальное значение выпрямленной ЭДС  (при угле =0)

В.

3) В соответствии с (1.50) с учетом выражения (1.57), где =6, определяется ток нагрузки:

.

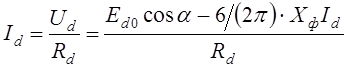После несложных преобразований последнего выражения окончательно рассчитывается ток нагрузки

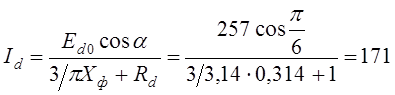А.

4) По выражению (1.52) при = 3 и, определяется ток входящего в работу вентиля на интервале коммутации, например вентиля  в группе с ОК,

.

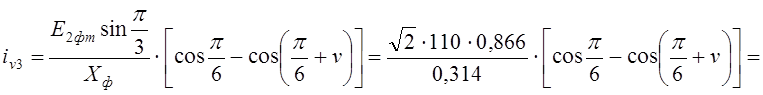
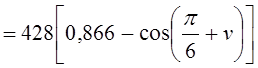5) По выражению (1.53) рассчитывается ток вентиля, выходящего из работы, например вентиля  в группе с ОК ,

.

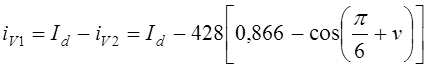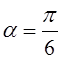6) В соответствии с выражением (1.55) при =3 и , определяется угол коммутации:

.

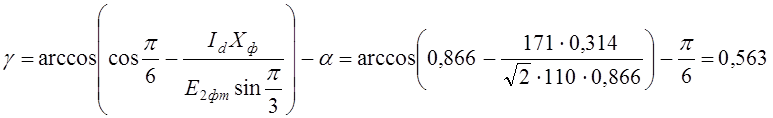7) В соответствии с (1.57), где = 6 и 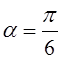, записывается уравнение внешней характеристики

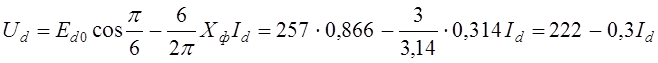, по которому строится внешняя характеристика (рис.1.25).

8) По результатам расчета строятся кривые мгновенных значение токов вентилей ,  (см. рис. 1.1) и кривая мгновенного значения выпрямленного напряжения в группе с OK . Аналогично строится кривая мгновенных значений выпрямленного напряжения в группе с ОА . В соответствии с (1.56) выпрямленные напряжения вентильных груш на интервалах коммутации равны полусумме вторичных фазных ЭДС , коммутирующих фаз. Кривая  мгновенных значений выпрямленного напряжения на выходе моста находится путем суммирования с учетом знаков мгновенных выпрямленных напряжений  и  вентильных групп. Кривые мгновенных значений токов и напряжений приводятся на рис. 1.24.

Рис. 1.24. Токи и напряжения в мостовой схеме с =3

Следует отметить, что явление коммутации не ухудшает коэффициент полезного действия преобразователя. Это связано с тем, что энергия, обусловленная коммутационным падением напряжения, не преобразуется в тепло, так как падение напряжения происходит не на активном сопротивлении силовой части, а на индуктивных сопротивлениях электромагнитного рассеяния фаз трансформатора.

Рис.1.25. Внешняя характеристика трехфазной мостовой схемы