
















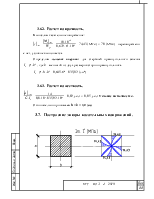
расчетному сопротивлению срезу, выразим требуемый для выполнения условия прочности полярный момент сопротивления сечения:
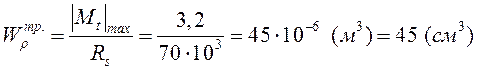
Величина требуемого полярного момента сопротивления сечения обеспечивает выполнение условия прочности, она зависит от максимального крутящего момента в опасном сечение и от расчетного сопротивления срезу. И не зависит от формы поперечного сечения.
Для круглого сечения полярный момент
инерции: 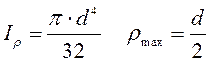 , тогда полярный момент
сопротивления сплошного круглого сечения:
, тогда полярный момент
сопротивления сплошного круглого сечения:
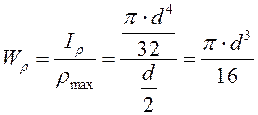 ;
;
Приравниваем 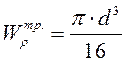 и
выражаем диаметр:
и
выражаем диаметр:
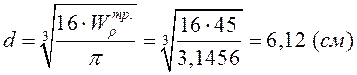
Вычисляем с этим диаметром значение наибольшего по модуля касательного напряжения:
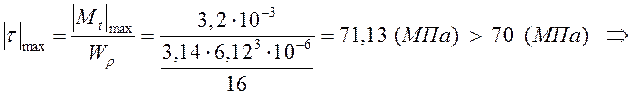 перенапряжение, найдем
процент перенапряжения:
перенапряжение, найдем
процент перенапряжения:
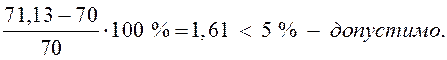
Определим момент инерции:
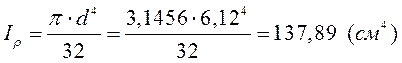
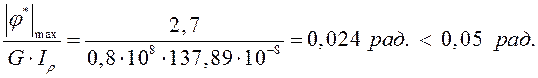 Условие выполняется.
Условие выполняется.
Окончательно принимаем d = 6,12 (см)
Площадь сплошного круглого сечения: 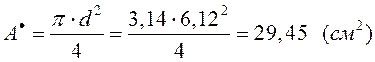
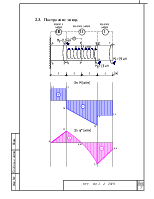
 Построение эпюры касательных напряжений.
Построение эпюры касательных напряжений.Полярный момент инерции: 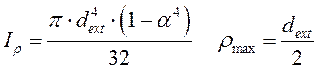 , тогда полярный момент сопротивления
трубы:
, тогда полярный момент сопротивления
трубы:
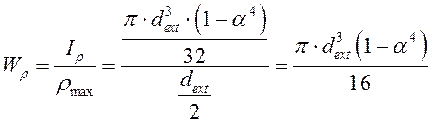 ;
;
Приравниваем 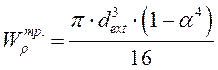 и
выражаем диаметр:
и
выражаем диаметр:
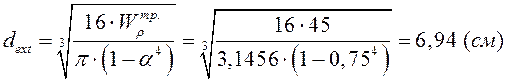
Вычисляем с этим диаметром значение наибольшего по модуля касательного напряжения:
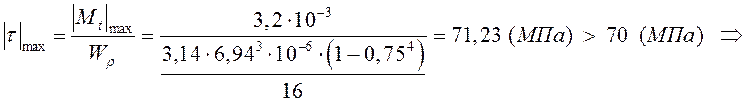 перенапряжение,
найдем процент перенапряжения:
перенапряжение,
найдем процент перенапряжения:
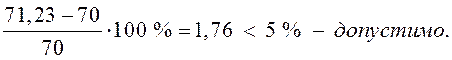
Определим момент инерции трубчатого сечения:
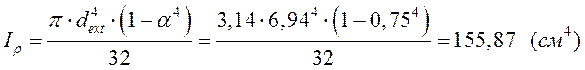
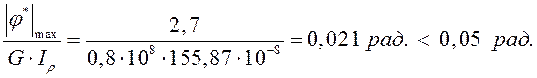 Условие выполняется.
Условие выполняется.
Окончательно принимаем d = 6,94 (см)
Площадь трубчатого сечения:
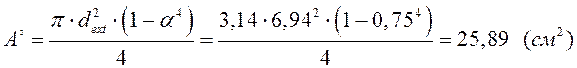
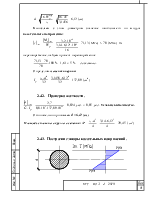
 Построение эпюры касательных напряжений.
Построение эпюры касательных напряжений.При кручении прямоугольных сечений используют следующие геометрические характеристики:
Момент инерции ![]() и момент сопротивления
и момент сопротивления ![]()
В данном случае h/b = 2 по табл.[1]
в зависимости от отношения высоты к ширине сечения берем: ![]()
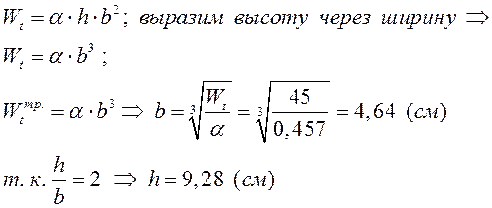
Вычислим касательное напряжение:
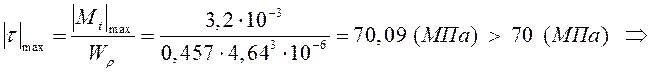 перенапряжение, найдем
процент перенапряжения:
перенапряжение, найдем
процент перенапряжения:
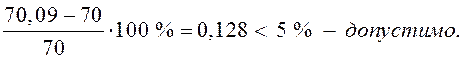
Определим момент инерции: для
стержней прямоугольного сечения ![]() , где b – меньший из двух размеров сторон прямоугольника.
, где b – меньший из двух размеров сторон прямоугольника.
![]()
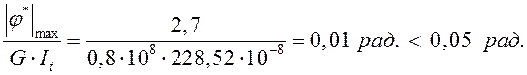 Условие выполняется.
Условие выполняется.
Окончательно принимаем h = b = 4,64 (см)
![]()
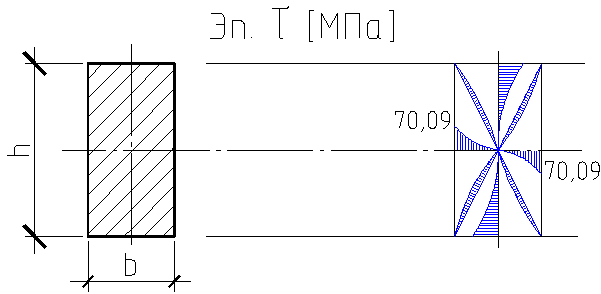 Построение эпюры касательных напряжений.
Построение эпюры касательных напряжений.![]() С экономической точки зрения, в данном
варианте, выгодным является использовать круглое сплошное сечение
С экономической точки зрения, в данном
варианте, выгодным является использовать круглое сплошное сечение
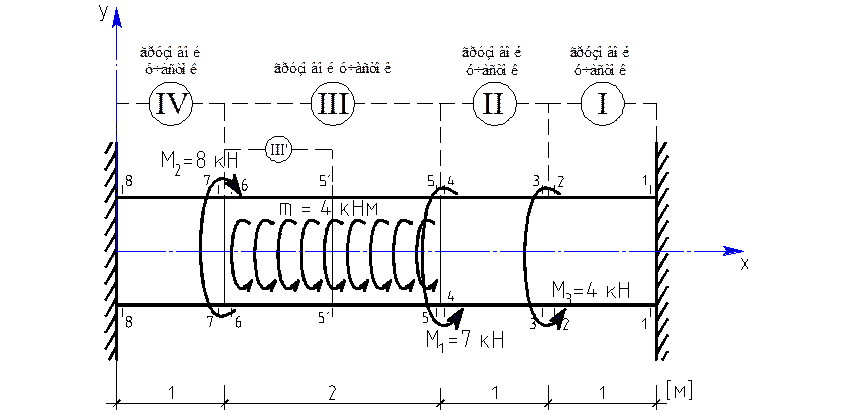 Статически неопределимая задача.
Статически неопределимая задача.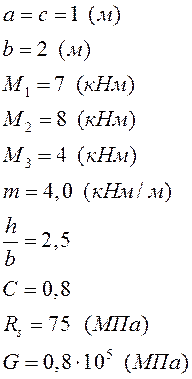 |
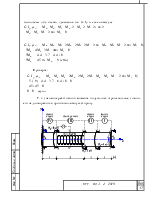
Назначим систему координат, разобьем стержень
на грузовые участки, отбросим заделку справа и заменим её влияние реактивным
моментом ![]() .
.
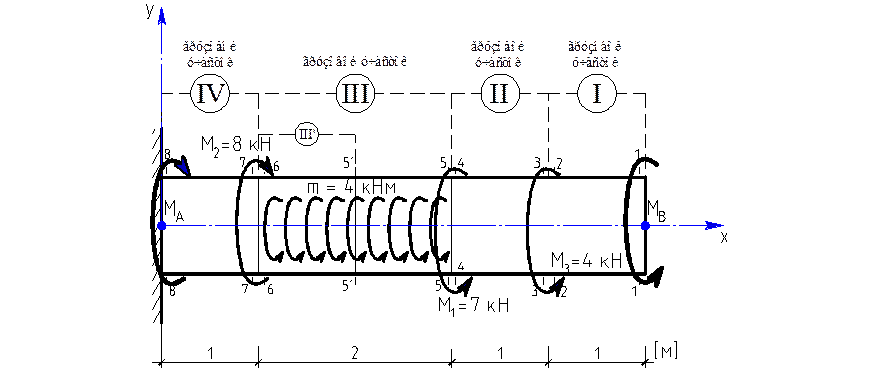 Статическая сторона задачи.
Статическая сторона задачи.Составим уравнение равновесия:
![]()
Найдем степень статической неопределимости как
разницу между неизвестными опорными реакциями и количеством уравнений статики ![]() - степень статической неопределимости
равна единице. Это значит, что задача один раз статически неопределима и для
раскрытия статический неопределимости необходимо привлечь еще одну сторону
задачи.
- степень статической неопределимости
равна единице. Это значит, что задача один раз статически неопределима и для
раскрытия статический неопределимости необходимо привлечь еще одну сторону
задачи.
Перемещение (угол закручивания) свободного
конца (сечение 1 – 1 - жесткая заделка) невозможно, тогда это перемещение можно
представить как сумму углов закручивания грузовых участков ![]()
Угол закручивания на грузовом участке длинной l, где ![]() можно представить в виде:
можно представить в виде: 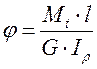 ;
;
Т. к. в данном случае на III грузовом участке присутствуют равномерно распределенные крутящие моменты получим формулу для перемещения:
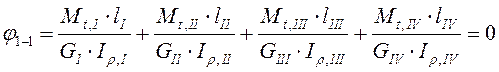
Запишем уравнения крутящих моментов на
грузовых участках, рассматривая при этом равновесие правой части, содержащей
опорную реакцию ![]() .
.
![]()
![]()
![]()
![]()
Подставим эти выражения в уравнение совместности деформаций, тогда зная, что крутильная жесткость на грузовых участках не меняется, получим уравнение с одним неизвестным:
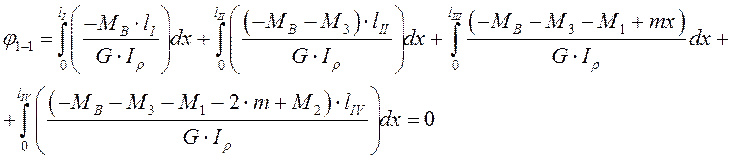
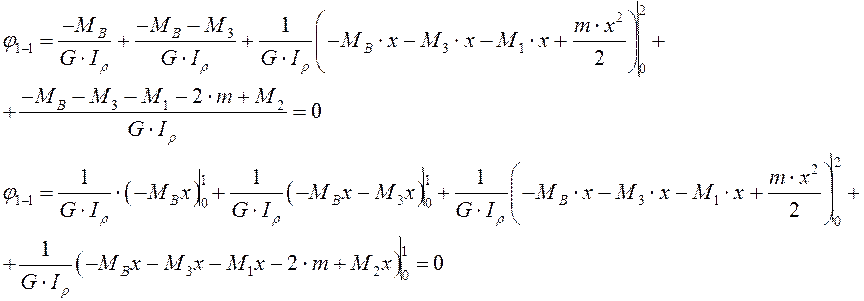 |
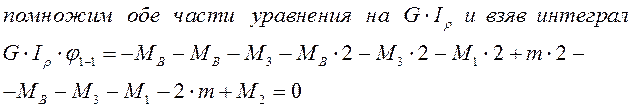
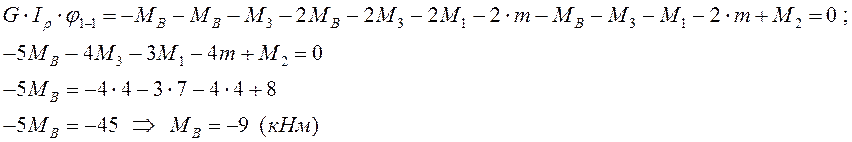
Проверка:
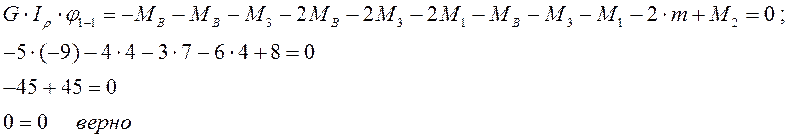
Т. к. значение реактивного момента получилось отрицательное, значит, его надо направить в противоположную сторону.
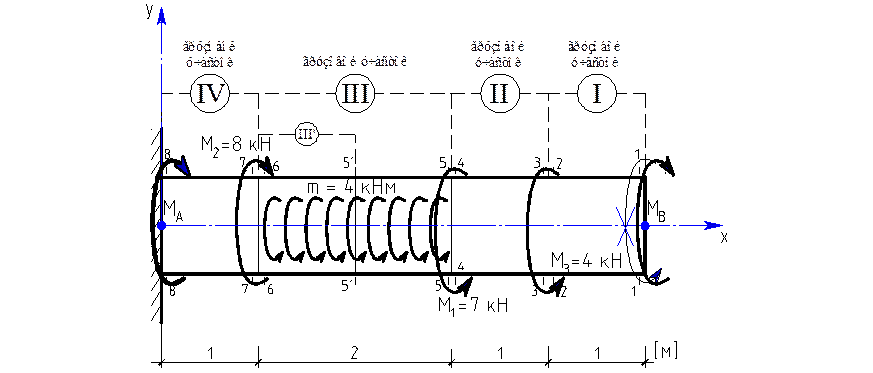 |
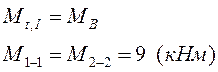
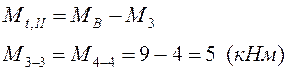
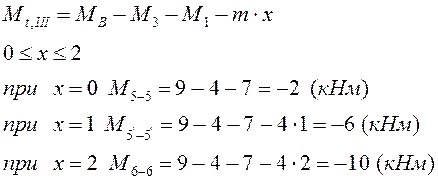
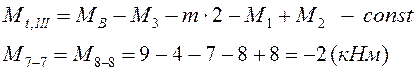
Определение углов закручивания начинают с того сечения, в котором известен начальный угол закручивания, в данном случае это сечение 8 – 8 (заделка). Угол закручивания здесь равен 0, т.к. жесткая заделка.
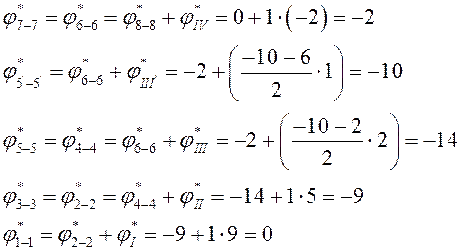
Перемещение сечение 1 – 1 равно нулю, так как этому сечению соответствует заделка, а в ней поворот невозможен.
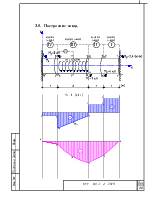
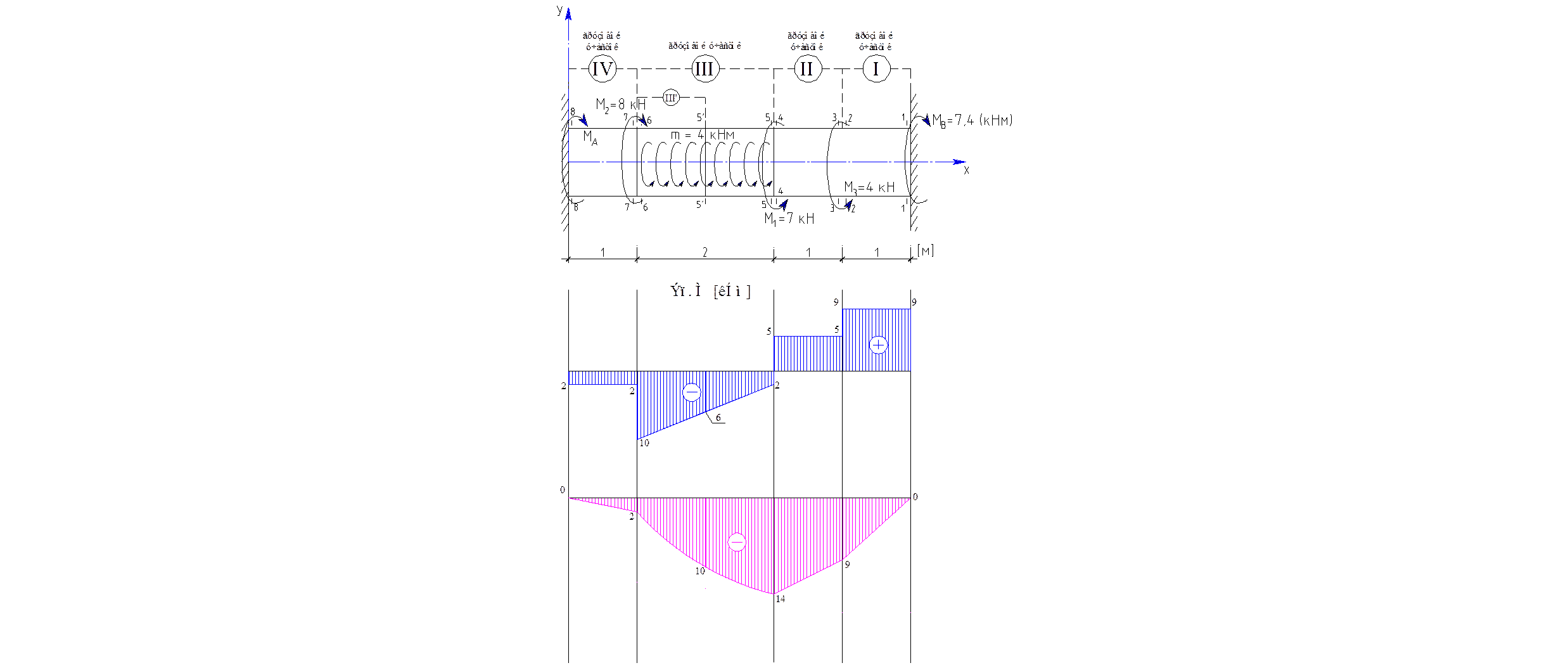 Построение эпюр.
Построение эпюр.С помощью эпюры крутящих моментов определим
опасное сечение. В сечении 6 – 6 на II грузовом
участке максимальный крутящий момент: ![]() .
.
Уравнение прочности: 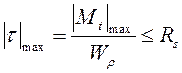
Приравниваем максимальное по модулю касательное
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.