







Содержание
1. Введение. 2
1.1. Построение эпюр внутренних силовых факторов в балке и раме. 2
1.1.1. Определение опорных реакций. 2
1.1.2. Построение эпюр внутренних усилий. 2
1.1.3. Правила знаков. 3
1.1.4. Правила. 4
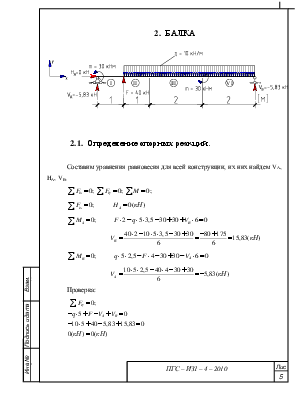
2. Балка. 5
2.1. Определение опорных реакций. 5
2.1.1. Определение внутренних усилий на грузовых участках. 6
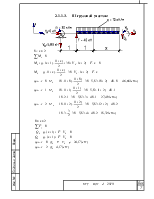
2.1.1.1.I грузовой участок: 6
2.1.1.2.II грузовой участок: 6
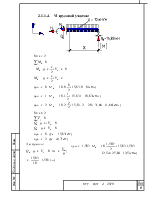
2.1.1.3.III грузовой участок: 7
2.1.1.4.VI грузовой участок: 8
2.2. Построение эпюр внутренних усилий. 9
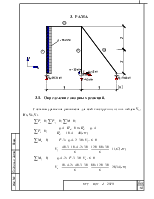
3. Рама. 10
3.1. Определение опорных реакций. 10
3.1.1. Определение внутренних усилий на грузовых участках. 11
3.1.1.1.I грузовой участок: 11
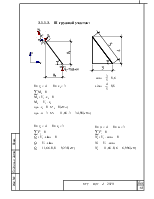
3.1.1.2.II грузовой участок: 12
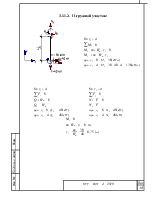
3.1.1.3.III грузовой участок: 13
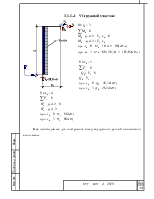
3.1.1.4.VI грузовой участок: 14
3.2. Построение эпюр внутренних усилий. 15
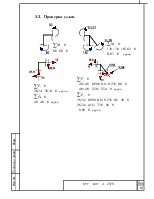
3.3. Проверка узлов. 16
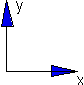
Необходимо назначить глобальную систему координат. Обозначить на чертеже вертикальные (V) и горизонтальные (H) составляющие опорных реакций. Найти опорные реакции. Выделить грузовые участки.
Грузовой участок – часть стержня, в пределах которого внутренние усилия подчиняются одному закону (описывается одним уравнением)
Эпюра внутреннего усилия – график функции описывающей внутреннее усилие.
Под действием внешних нагрузок (сосредоточенные и равномарно распределенные нагрузки и моменты) элементы сооружения деформируются и в них возникают внутренние усилия. Выделяют: продольные и поперечные усилия, крутящие и изгибающие моменты. Как в балке, так и в раме возникают поперечные и продольные усилия и изгибающие моменты.
Для построения эпюр необходимо для каждого внутреннего усилия на всех грузовых участках составить уравнения. Для этого используем метод сечения:
· Рассматриваемы элемент мысленно рассекаем плоскостью на две части.
· Одну отбрасываем, а действие другой (отброшенной) заменяем противоположно направленными внутренними усилиями Q, M.
· Составляем уравнения статики.
· Находим значения внутренних усилий.
 Правила знаков.
Правила знаков.Продольные внутренние усилия (N) – положительны при растяжении
- отрицательны при сжатии
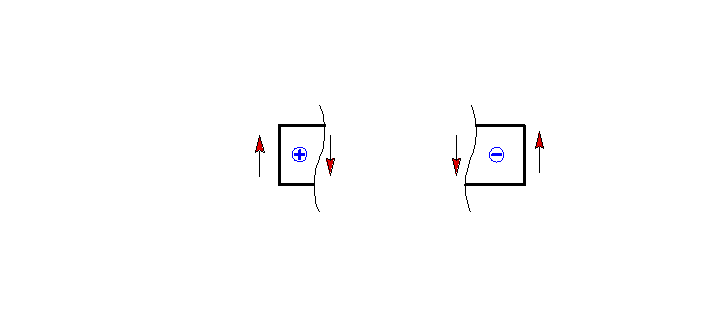 Продольное
внутреннее усилие в любом сечении равно алгебраической сумме проекций
всех внешних сил взятых по одну сторону от сечения на продольную ось стержня.
Продольное
внутреннее усилие в любом сечении равно алгебраической сумме проекций
всех внешних сил взятых по одну сторону от сечения на продольную ось стержня.
Поперечные внутренние усилия (Q) - положительны при стремлении вращать отсеченную часть по часовой стрелке
- отрицательны - против часовой
Поперечное внутреннее усилие в любом сечении равно алгебраической сумме проекций всех внешних сил взятых по одну сторону от сечения на поперечную ось стержня.
Изгибающие моменты (M) – положительны если растягивают нижние волокна;
- отрицательны если растягивают верхние.
Так же изгибающие моменты будут положительные если направление момента совпадает с направлением оси координат и отрицательные в противном случае.
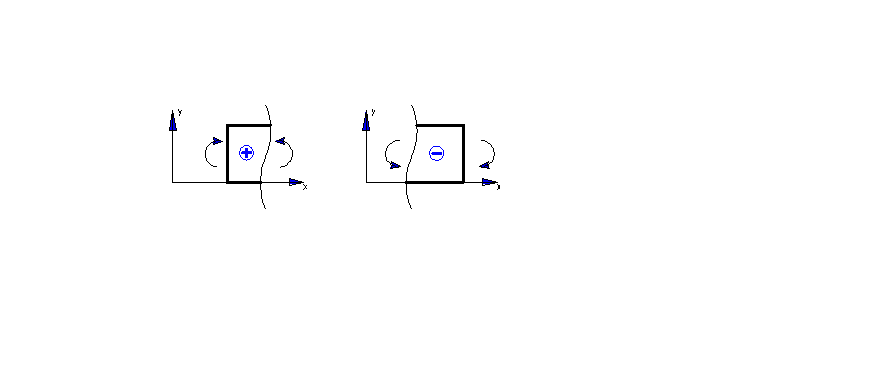 Изгибающий момент в любом сечении равен алгебраической сумме моментов
всех внешних сил, взятых по одну сторону от сечения относительно центра тяжести
поперечного сечения стержня.
Изгибающий момент в любом сечении равен алгебраической сумме моментов
всех внешних сил, взятых по одну сторону от сечения относительно центра тяжести
поперечного сечения стержня.
Эпюру изгибающих моментов строят на РАСТЯНУТЫХ ВОЛКНАХ, знак на эпюру не ставят.
Если на расчетной схеме приложена сосредоточенная сила, то на эпюре поперечных сил (Q) соответственно в этом сечении бадет скачок равный величине этой силы, а на эпюре изгибающих моментах (M) – излом.
Под сосредоточенными моментами на эпюре моментов – скачок равный величине этого момента.
Грузовому участку, в пределах которого действует равномерно распределенная нагрузка, на эпюре поперечной силы соответствует участок с наклонной прямой (прямая зависимость), а на эпюре моментов – парабола (квадратичная зависимость).
При построении эпюр необходимо строго следить за выполнением дифференциальных зависимостей:
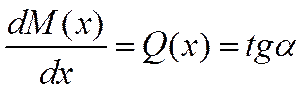
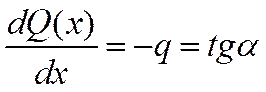
Геометрическим смыслом первой производной функции является тангенс угла наклона касательной к графику функции. В случае, когда первая производная обращается в ноль, функция имеет экстремум.
При построении эпюр изгибающих моменто, имеющих участки с параболой, необходимо соблюдать правило «Паруса». Оно сводится к тоиу, что равномерно распределенная нагрузка условно принимается за ветер, а парабола – за парус. Куда дует ветер, туда и прогибается парус.
 Балка
БалкаСоставим уравнения равновесия для всей конструкции, их них найдем VA, HA, VB,
![]()
![]()
![]()
![]()
![]()
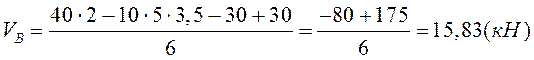
![]()
![]()
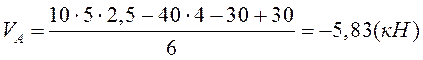
Проверка:
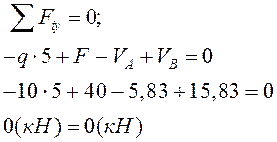
 I грузовой участок:
I грузовой участок:
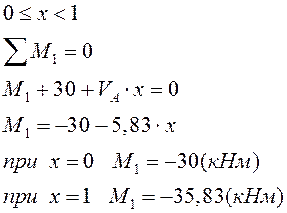
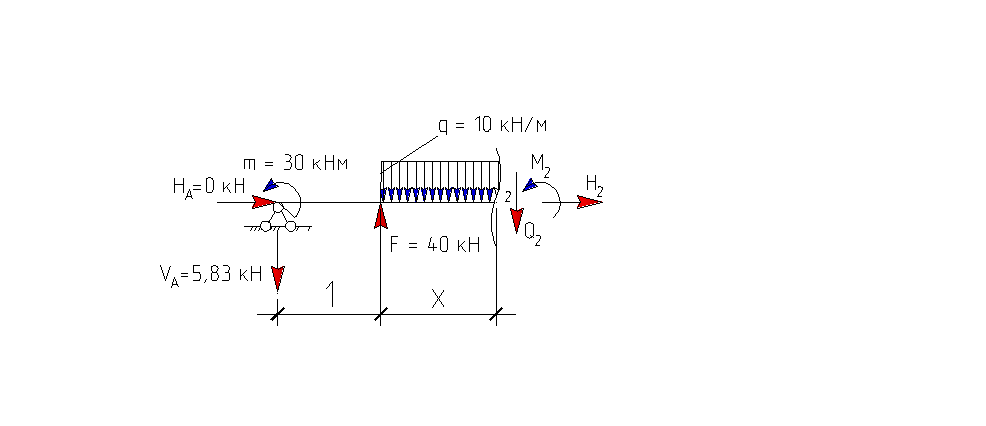
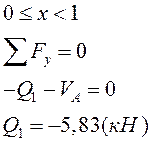

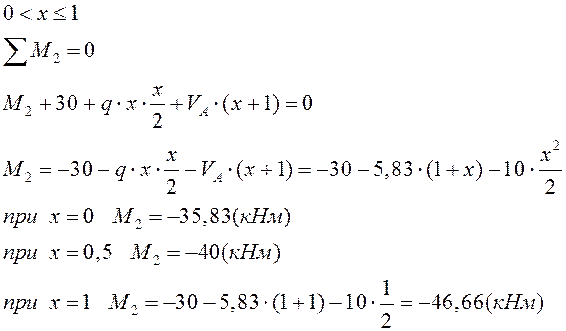
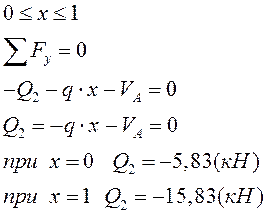
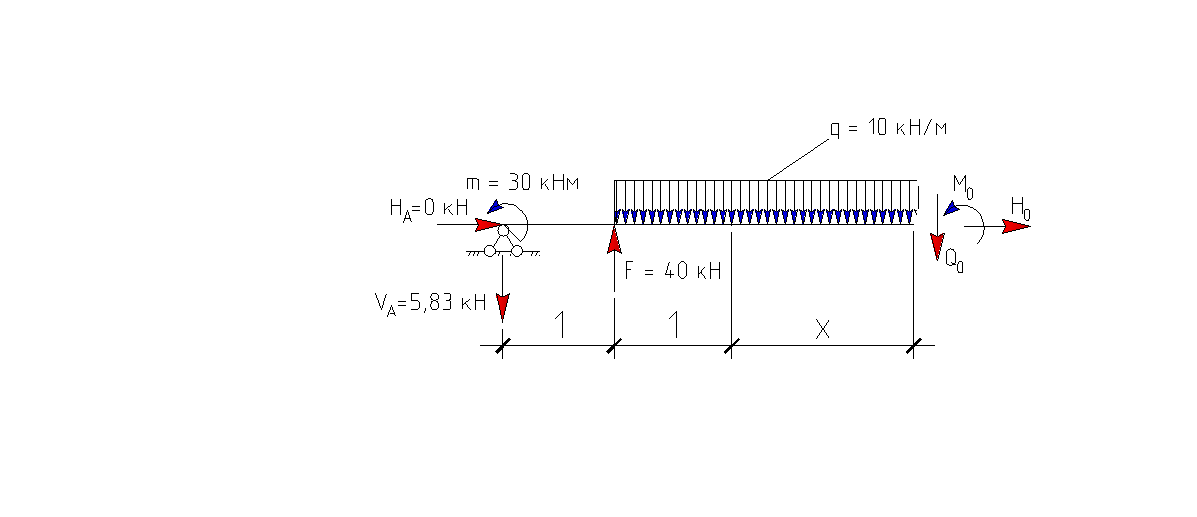 III грузовой участок:
III грузовой участок: |
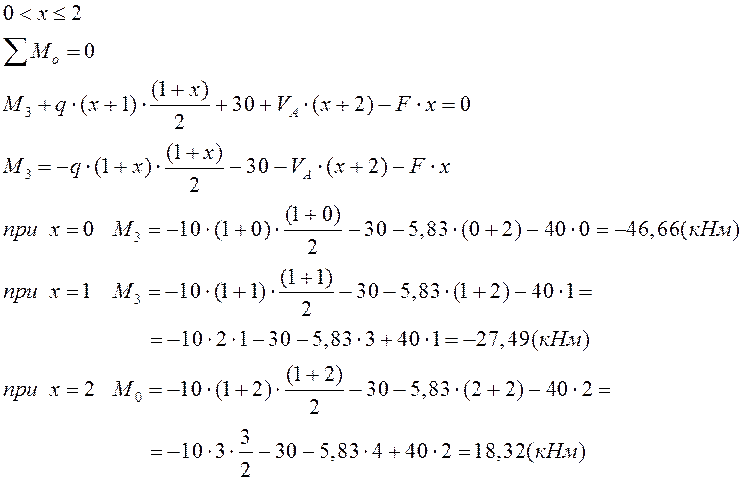
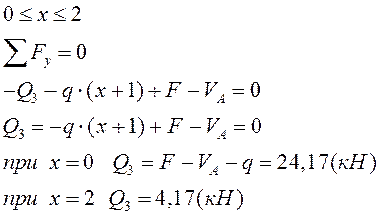
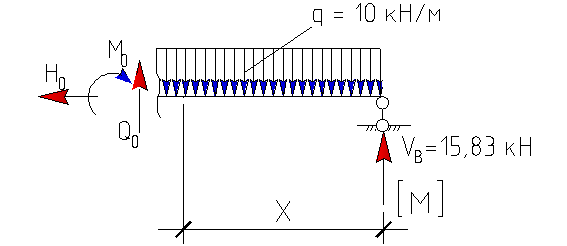 VI грузовой
участок:
VI грузовой
участок: |
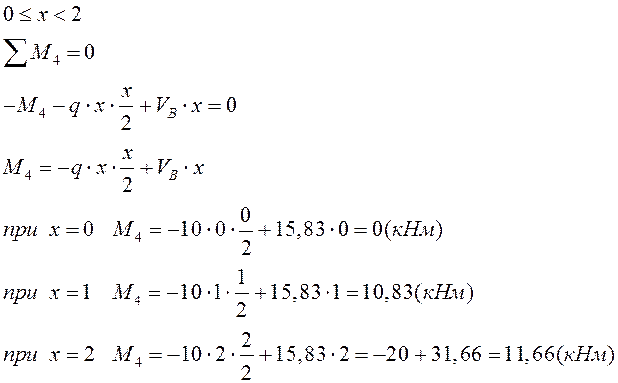
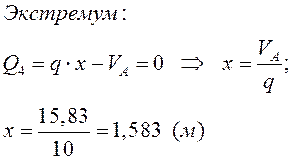
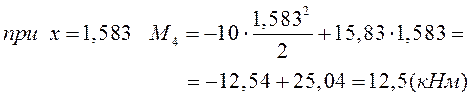
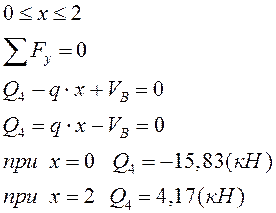
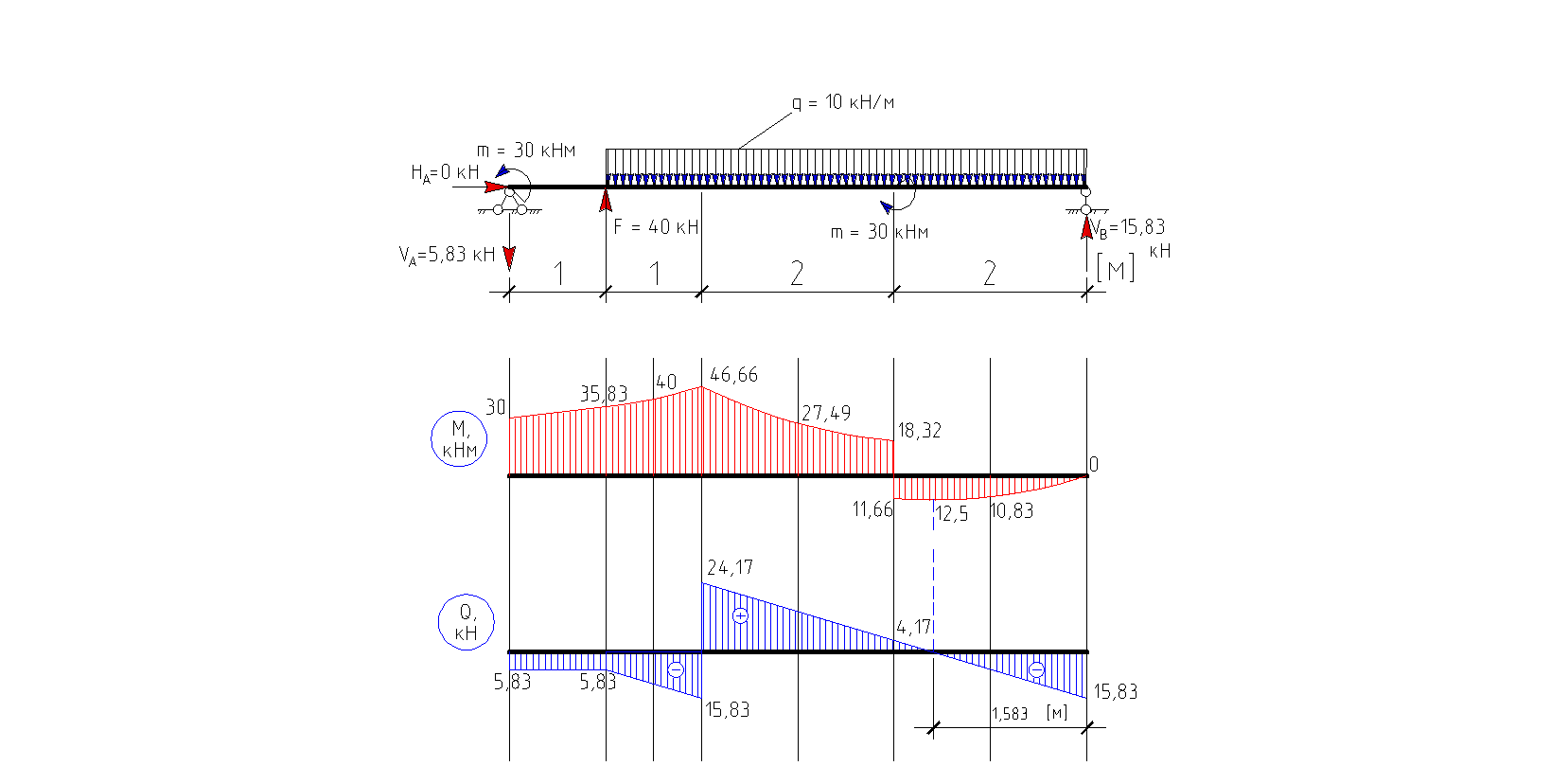 По найденным значениям строим эпюры:
По найденным значениям строим эпюры:

Составим уравнения равновесия для всей конструкции, из них найдем VA, HВ, VB, VC
![]()
![]()
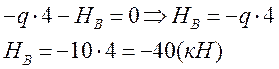
![]()
![]()
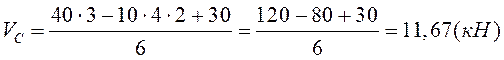
![]()
![]()
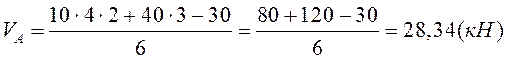
Проверка:
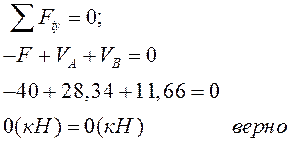
![]()
![]()
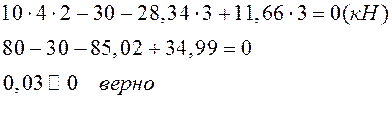
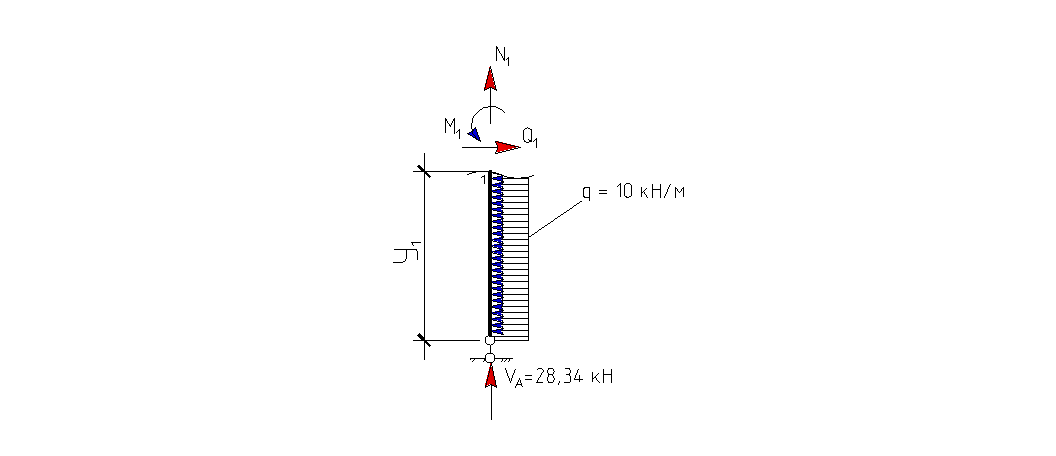 I грузовой участок:
I грузовой участок: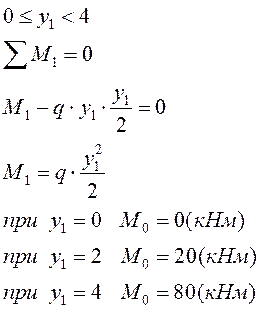

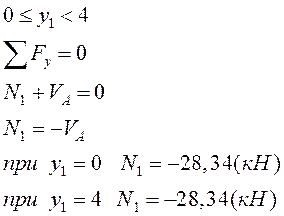
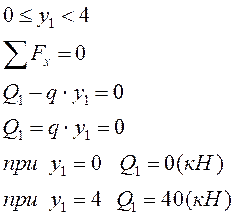
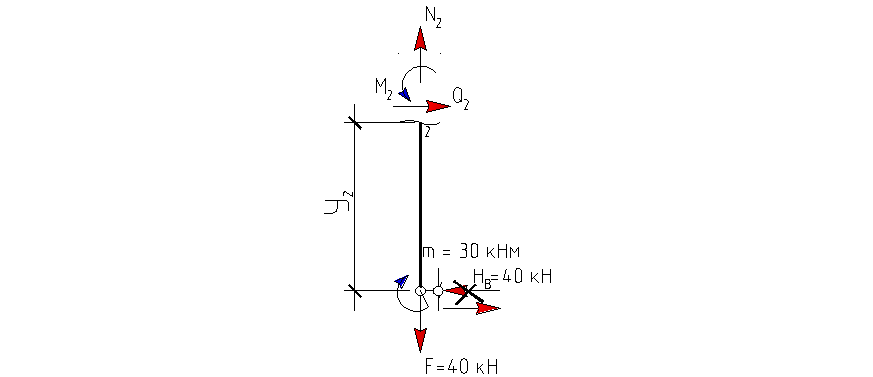 II грузовой участок:
II грузовой участок:
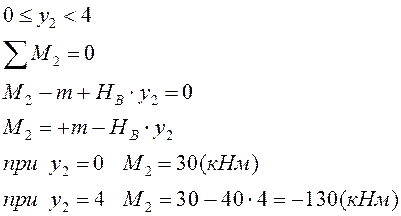
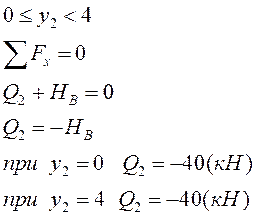
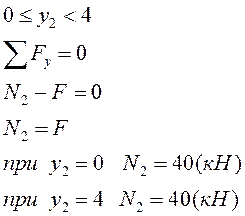
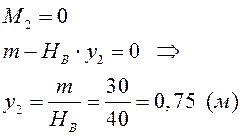 |
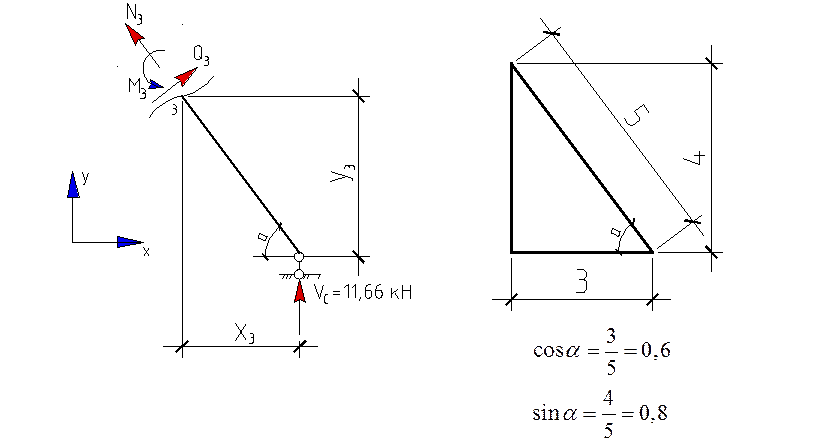 |
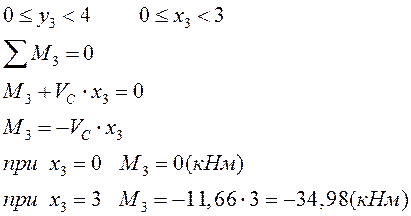
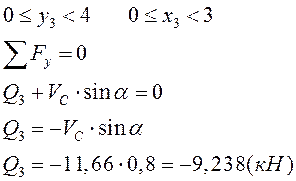
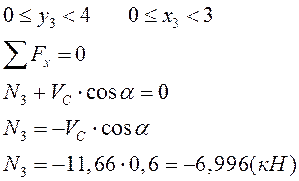
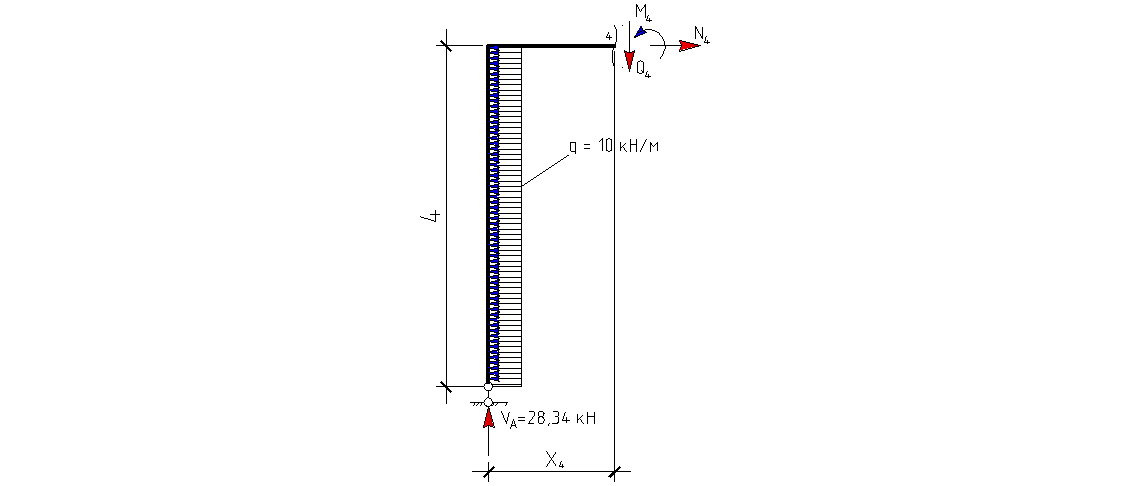 VI
грузовой участок:
VI
грузовой участок: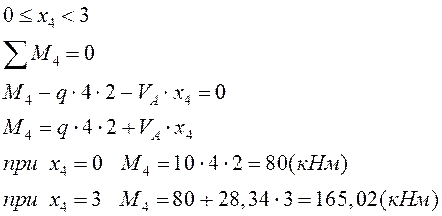 |
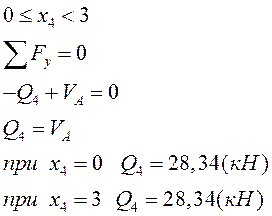
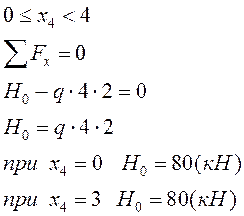
Все необходимые для построения эпюр внутренних усилий вычислении выполнены.
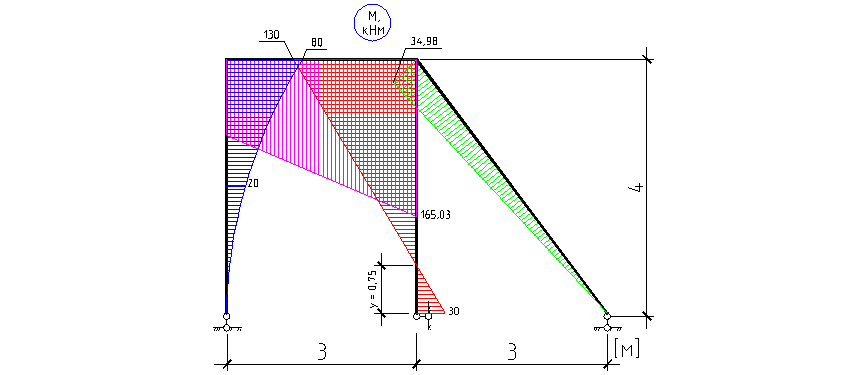 Построение эпюр внутренних усилий.
Построение эпюр внутренних усилий.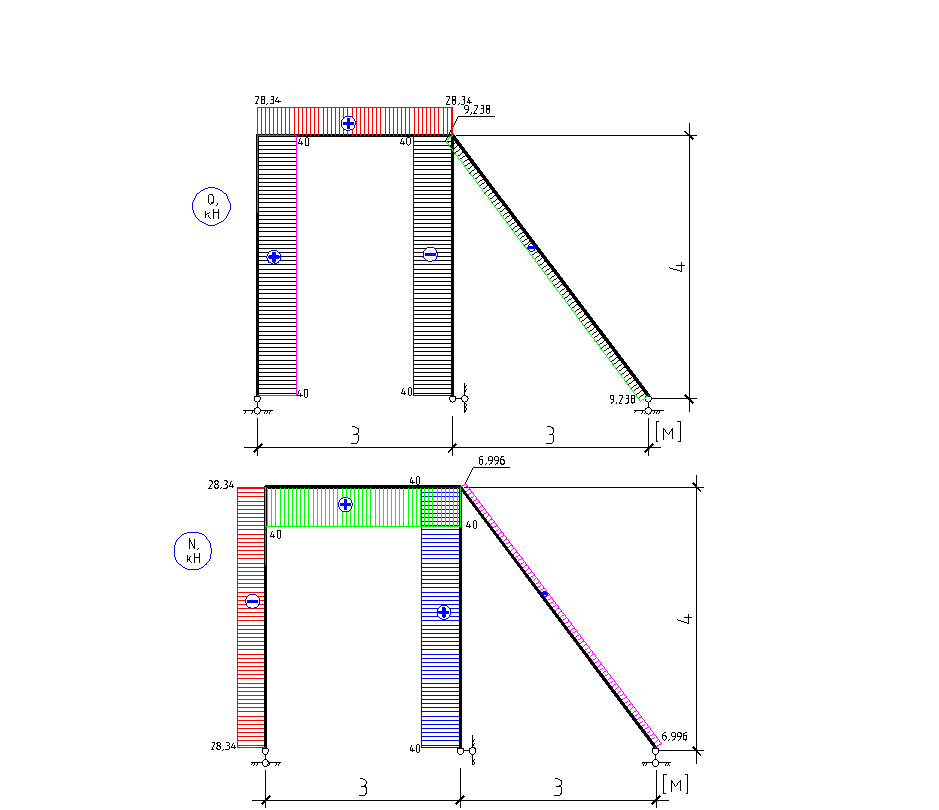

 Проверка
узлов.
Проверка
узлов.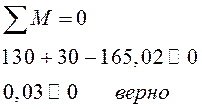 |
|||
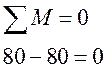 |
|||


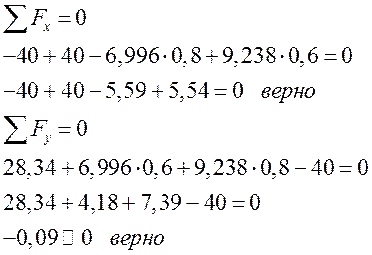 |
|||
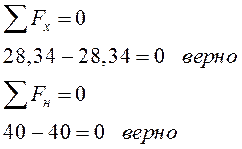 |
|||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.