Система слежения за задержкой. Основные параметры устройства, передаточные функции

Федеральное государственное образовательное учреждение высшего профессионального образования

«Сибирский Федеральный Университет»

Институт инженерной физики и радиоэлектроники

Кафедра «Приборостроение и наноэлектроники»

КУРСОВАЯ РАБОТА

«Система слежения за задержкой»

Пояснительная записка

                                                                                                          Выполнил:

ст. гр. РТ07-11

                                                                                                         Проверил:

КРАСНОЯРСК

2010 г.

ЗАДАНИЕ

по курсовому проектированию

1.  Тема курсовой работы:              Система слежения за задержкой (ССЗ)

2.  Срок сдачи законченной работы:

3.  Исходные данные к работе:

а) Номер варианта: №1

б) Параметры задающего воздействия: , в) Спектральная плотность шума:

г) Коэффициент передачи дискриминатора:

д) Параметры динамического звена: 

е) Следящий измеритель дальности некогерентной импульсной РЛС (сложный ФМ сигнал)

Содержание расчетно – пояснительной записки:

1)  Передаточные функции разомкнутой и замкнутой системы………………………….2

2)  Оптимизация следящей системы………………………………………………………...4

3)  Определение запаса устойчивости системы………………….…………………………8

4)  Моделирование следящей системы на ЭВМ…………………………………………..10

Вывод……………………………………………………………………………………..16

Литература……………………………………………………………………………….17

1.ПЕРЕДАТОЧНЫЕ ФУНКЦИИ РАЗОМКНУТОЙ И ЗАМКНУТОЙ СИСТЕМЫ

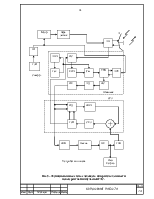
Структурная схема следящей системы имеет вид:

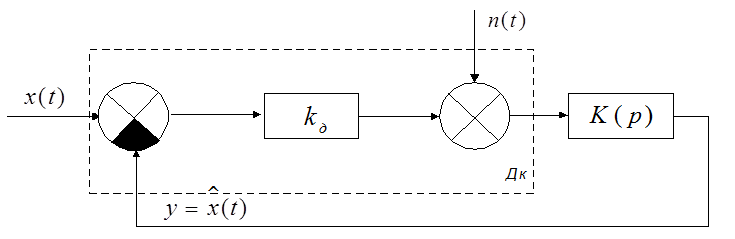
Рис.1

Дк – дискриминатор; x(t) – модель задающего воздействия; n(t) – помеха в          виде белого шума; K_д – коэффициент передачи дискриминатора; K(p) – передаточная функция динамического звена

Структура и параметры динамического звена определяются общей передаточной функцией:

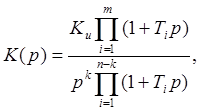                                                                                              (1)

где      k - число интеграторов;

K_и – общий коэффициент передачи k интеграторов;

m – число форсирующих звеньев;

n-k – число инерционных звеньев;

n – порядок дифференциального уравнения, описывающего систему.

При k=2, n=2, m=1 передаточная функция динамического звена определяется выражением (2).

                                                                                        (2)

Передаточная функция разомкнутой системы:

                                                                            (3)

Определим спектральную плотность эквивалентного шума n_Э(t) приведенного ко входу дискриминатора. Преобразуем структурную схему: перенесем сумматор на вход безынерционного звена.

Передаточная функция замкнутой системы:

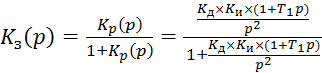
                                                                               (4)

Воспользуемся правилом переноса сумматора с выхода на вход звена. После преобразования получим схему:

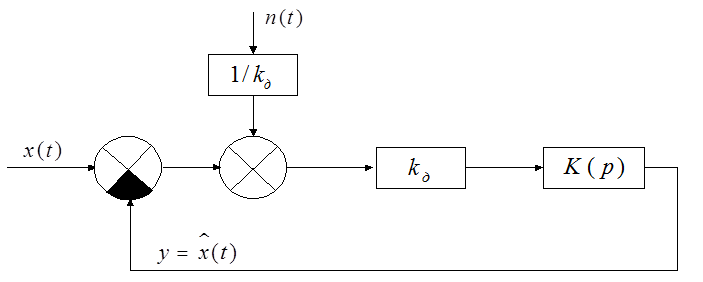
Рис.2

Тогда спектральная плотность имеет вид:

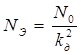                                                                                                         (5)

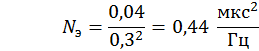
2.ОПТИМИЗАЦИЯ ПАРАМЕТРОВ СИСТЕМЫ

Оптимизация системы производится по критерию минимума среднего квадрата ошибки сводится к нахождению значения параметра  , при котором обеспечивается минимум величины:

                                                                                           (6)

где     динамическая ошибка, обусловленная инерционностью следящей системы;

 - дисперсия шумовой ошибки, обусловленная помехой n(t).

Так как порядок астатизма рассматриваемой системы равен двум, поэтому динамическая ошибка определяется параметром  задающего воздействия.

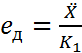                                                                                                               (7)

где   - добротность системы по ускорению.

Случайная составляющая e_n(t) ошибки определяется статистическими характеристиками помехи n(t), структурой и параметрами системы.

Дисперсия шумовой ошибки:

                                                                                       (8)

где 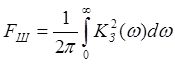   - шумовая полоса следящей системы в Гц;

Передаточная функция замкнутой системы определяется выражением:

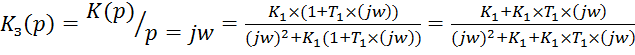                  (9)

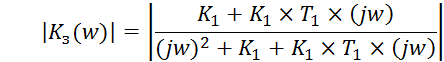
                                                                          (10)

Для упрощения вычисления интеграла шумовой полосы выражение для квадрата модуля коэффициента передачи представлено в виде полиномов:

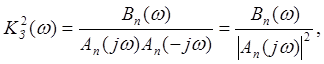                                                                 (11)

где полиномы A_n(jω) и B_n(jω) определяются как

;                                                                (12)

Приравнивая соответствующие коэффициенты, находим:

                                                                          (13)

                                                                      (14)

Шумовая полоса системы шумовой ошибки определяется как:

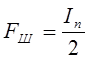                                                                                                       (15)

Значение I_n при n=2 определяется следующим образом:

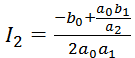                                                                                                   (16)

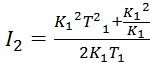
Тогда F_Ш:

Находим :

                                                                                                 (17)

Теперь можно определить оптимальное значение шумовой полосы Fш системы и минимально достижимую ошибку слежения. Для этого необходимо продифференцировать выражение по параметру Кu  и приравнять производную к нулю.

                                                                    (18)

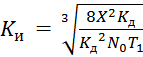
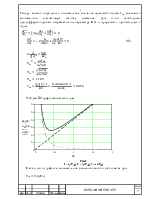
Найдем K_И графическим методом:

Рис.3

1 – e_d(F_Ш), 2 – σ_e(F_Ш), 3 – e²(F_Ш)

Как видно из графика, минимальное значение ошибки достигается при:

 (Гц)

3.ОПРЕДЕЛЕНИЕ ЗАПАСОВ УСТОЙЧИВОСТИ СИСТЕМЫ

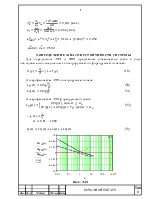
Для определения АЧХ и ФЧХ представим динамическое звено в виде последовательно соединенных интегрирующего и форсирующего звеньев:

                                                                               (19)

Логарифмическая АЧХ интегрирующего звена:

                                                                                          (20)

                                                                                           (21)

Логарифмическая АЧХ форсирующего звена:

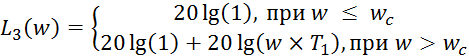                                       (22)

где 

                                                                (23)

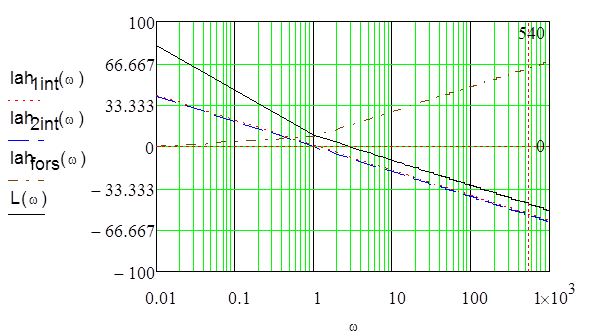
Рис.4 - ЛАХ 

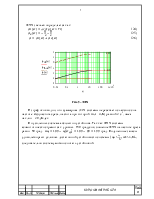
ФЧХ звеньев определяется как:

                                                                                   (24)

                                                                                                (25)

                                                                                         (26)

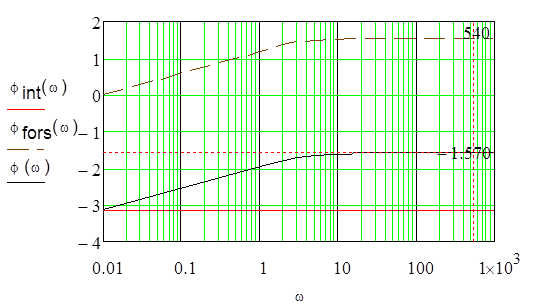Рис.5 – ЛФХ

Из графиков видно, что суммарная ЛАХ системы пересекает ось абсцисс на частоте  (частота среза, частота при которой ) равной 2 с^-1, имея наклон – 20 дБ/дек.

По усилению система абсолютно устойчива. Так как ФЧХ системы асимптотически стремится к уровню -180 градусов, значение ФЧХ на частоте среза равно -80 град.   град. Полученные запасы удоволетворяют условию достаточной устойчивости системы (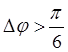, )., следовательно систему можно считать устойчивой.

4. МОДЕЛИРОВАНИЕ СЛЕДЯЩЕЙ СИСТЕМЫ

Дискретная передаточная функция цифровой модели следящей системы при использовании метода билинейного преобразования получается из передаточной функции замкнутой непрерывной системы  путем замены оператора непрерывного интегрирования:

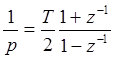  ,                                                                                                          (27)

где   - интервал дискретизации.

Интервал дискретизации выбирается в соответствии с теоремой Котельникова из условия:

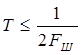                                                                                                       (28)

Передаточную функцию цифровой модели необходимо представить в виде:

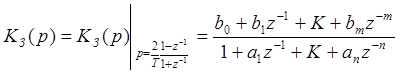                                                    (29)

Для определения характеристик следящей системы в переходном режиме разностное уравнение записывается в виде:

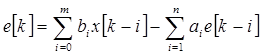                                                                          (30)

Коэффициенты этого разностного уравнения определяются по передаточной функции:

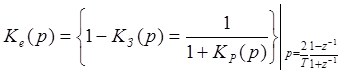 ,                                                           (31)

где      - дискретная передаточная функция для ошибки;

 - передаточная функция разомкнутой непрерывной системы.

                                                                                         (32)

                                                                                    (33)                    

                                                               (34)

=

, 

 ,    ,  

 ,

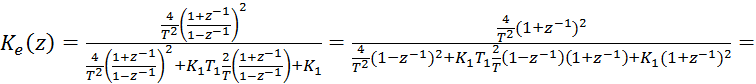
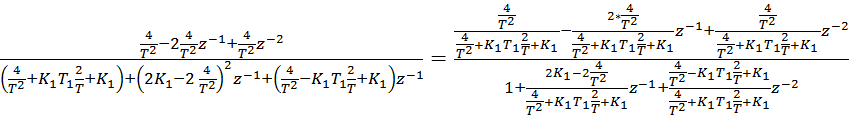
Получаем следующие коэффициенты:

b₀= 0.926

b₁= -1.853

b₂= 1.853

a₁= -1.849

a₂= 0.856

Ступенчатое воздействие определяется выражением:

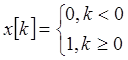                                                                                              (35)

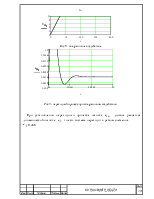
Отклик на ступенчатое воздействие имеет вид:

Рис 6 – график ступенчатого воздействия

Рис 7 – график переходного процесса

Как видно из графика переходный процесс – апериодический и, следовательно, перерегулирование равно нулю.

Время переходного процесса:

                                                                                  (36)

Произведем моделирование при линейном воздействии.

Формирование дискретных значений квадратичного воздействия производится по формуле:

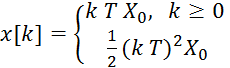                                                                                     (37)

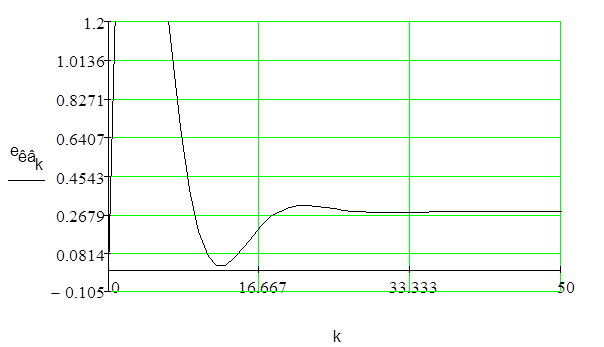Рис 8 – квадратичное воздействие

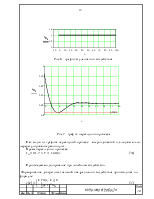
Рис9 - переходный процесс при квадратичном воздействии

При установлении переходного процесса ошибка екв  должна равняться